5. Уравнения Кирхгофа для цепи с индуктивно-связанными катушками

Положим, что между индуктивными катушками L₁ и L₃ (рис. 1) имеется индуктивная связь, заданная величиной взаимной индуктивности М. Включение L₁ и L₃ встречное, что показано точками возле катушек (одноименные зажимы). Для выбранных на рис. 1 направлений токов и направлений обхода контуров составим в общем виде систему уравнений Кирхгофа.

Интегро-дифференциальная форма:

Символическая форма:

Задание 2

Переходные процессы в линейных электрических цепях

Дана электрическая цепь, в которой происходит коммутация (рис. 4). В цепи действует постоянная ЭДС E. Параметры цепи приведены ниже.

Определить закон изменения во времени тока после коммутации в одной из ветвей схемы.

Задачу решить двумя методами: классическим и операторным. Построить график искомой величины на интервале от t=0 до t=3τ_max.

E=50 В;

L=2 мГн;

C=1670 мкФ;

R₁=1 Ом;

R₂=2 Ом;

R₃=2 Ом;

R₄=4 Ом;

^{_____________}

i₂=?

рис.4

1. Решение задачи классическим методом

Составим характеристическое уравнение

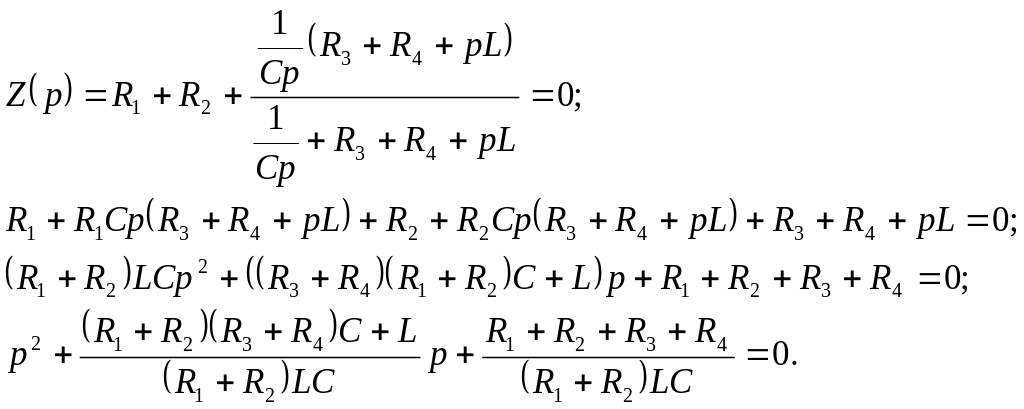
Подставив численные значения, получим:

Корни характеристического уравнения действительные и различные – переходный процесс апериодический и общее решение для u_с и i₂ имеет вид:

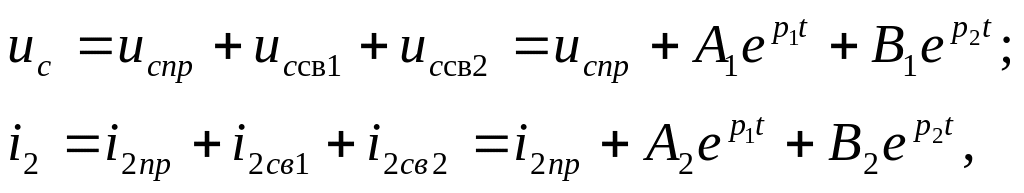
где u_cпр, i_2пр – принужденные (установившиеся) значения u_c и i₂.

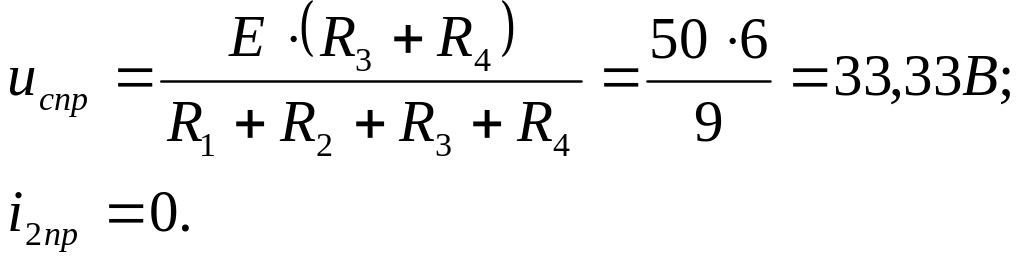
Найдем постоянные интегрирования A₁ и B₁.

1. На основе второго закона коммутации

Для момента t=0₊

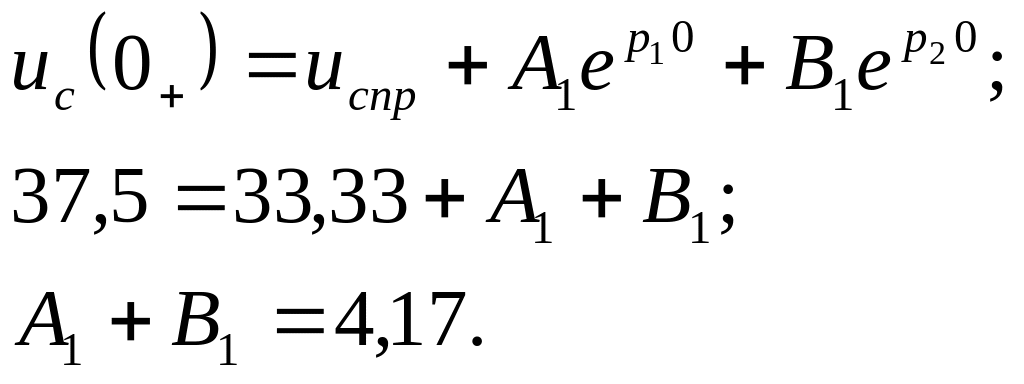
2. Для составления второго уравнения для A и B найдем

Вычислим ток i₂(0₊).

По первому закону Кирхгофа

В этой формуле для тока i₃(0₊) должен выполняться первый закон коммутации:

а ток i₁(0₊) найдем, используя второй закон Кирхгофа для левого контура (рис. 5):

откуда

тогда

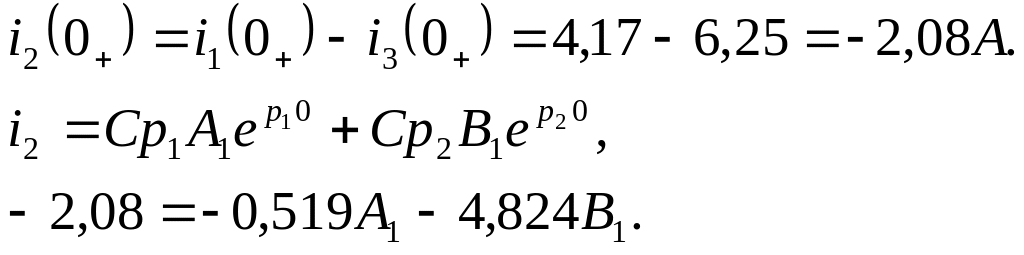
Объединяя уравнения (*) и (**) в систему, получим:

Ответ:

2. Решение задачи операторным методом

Составим схему замещения (рис. 5)

рис. 5

Как видно из схемы целесообразно использовать метод двух потенциалов. Заземлив узел 1, составим уравнение: Y₁₁(p)U₁(p)=I₁₁(p);

где Y₁₁ – узловая проводимость, I₁₁ – узловой ток.

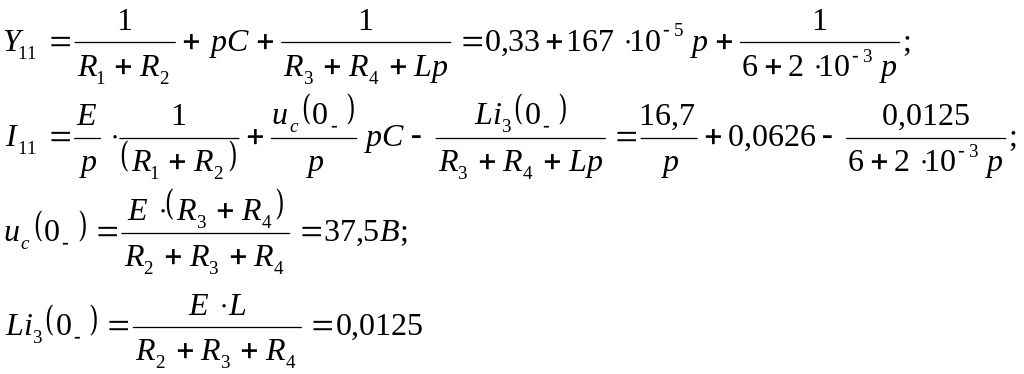
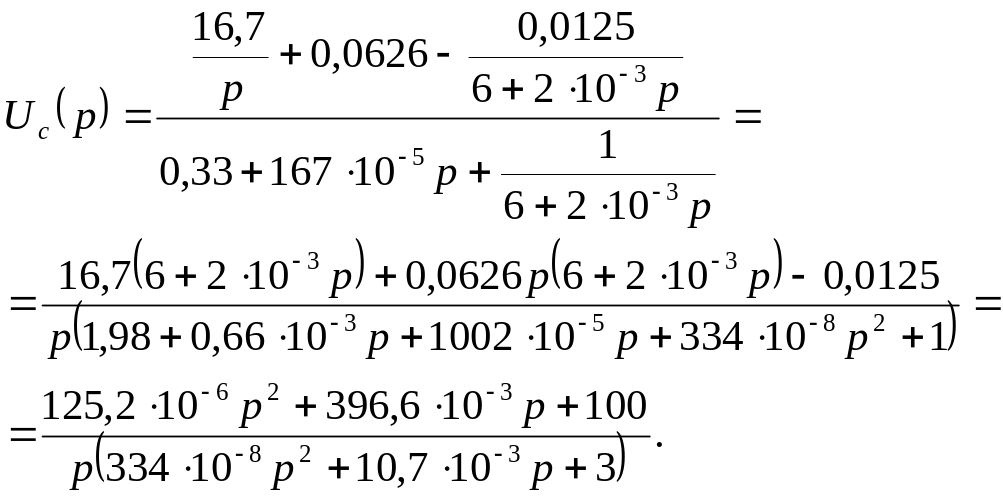
Получим изображение I₂(p), используя закон Ома для второй ветви (рис. 6):

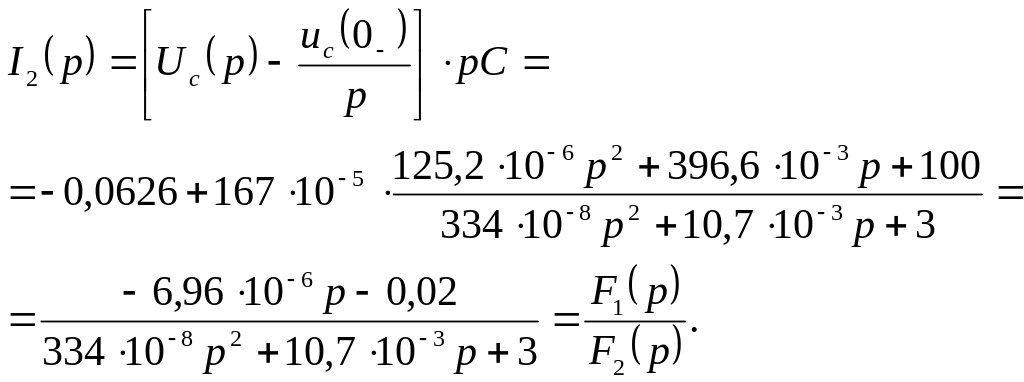
Формула разложения в таком случае имеет вид:

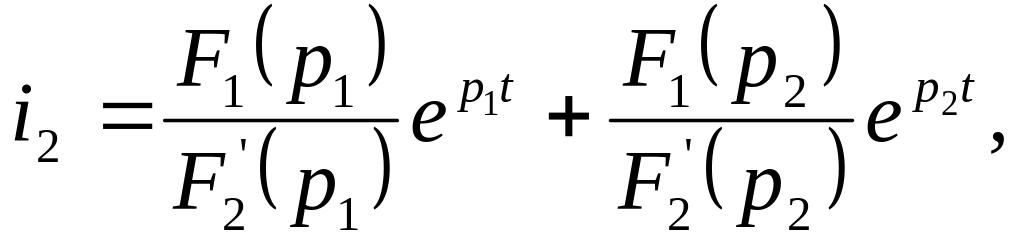
где p₁ и p₂ – корни уравнения F₂(p)=0

Уравнение F₂(p)=0 совпадает с характеристическим уравнением в классическом методе, его корни:

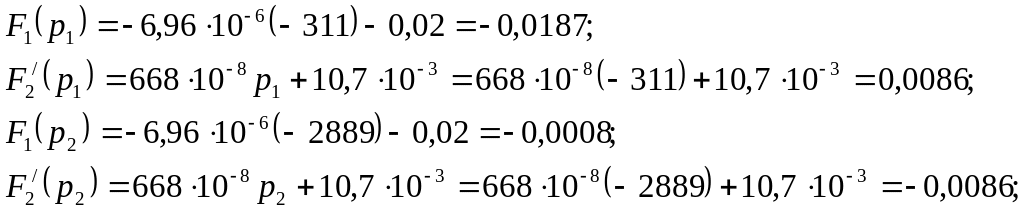
Графики переходного процесса для i₂ построены на рис. 6

рис. 6

Список литературы

1. Бессонов Л. А. Теоретические основы электротехники. – М.: Высшая школа, 1984.

2. Нейман Л. Р. Теоретические основы электротехники. – М., 1976.

3. Бессонов Л. А. Линейные электрические цепи. – М., 1974.

15