Министерство образования и науки РФ

Государственное образовательное учреждение высшего профессионального образования

«Ростовский государственный университет»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к лабораторной работе для студентов 1 курса физического факультета

ИЗУЧЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАЯТНИКА МАКСВЕЛА

Часть 3

Автор: Крыштоп В.Г. - доцент кафедры общей физики

Изучение динамики вращательного движения с помощью маятника максвелла

Работа посвящена изучению динамики твердого тела, не имею­щего закрепленных точек. На примере движения маятника Максвелла (рис. 1) рассмотрен случай плоского движения. Маятник Максвелла представляет собой диск, подвешенный на нити, нить намотана на ось диска.

Плоским называется движение, при котором траектории всех точек лежат в параллельных плоскостях. Движение тела в этом случае полностью определяется движением одного из его сечения в какой-либо из параллельных плоскостей.

Движение центра масс твердого тала определяется уравнением

(1)

где - скорость центра масс, - сумма всех внешних сил, действующих на тело.

Для того чтобы полностью определить движение тела, нужно кроме того написать уравнение моментов относительно какой-либо произвольно выбранной неподвижной оси (т.к. уравнение моментов справедливо для любой неподвижной оси).

(2) где - момент инерции твердого тела, - сумма моментов внешних сил.

Однако положение движущегося тела относительно неподвижной оси будет все время изменяться и связь между моментом импульса и угловой скоростью будет сложной.

Задача существенно упростится, если выбрать ось жестко связанную с телом. Но это значит, это мы составляем уравнение моментов в движущейся системе координат, которая при ускоренном движении тела окажется неинерциальной. В этой системе координат будут действовать силы инерции, и при составлении уравнения моментов должны быть учтены моменты сил инерции, что опять услож­нит задачу.

Однако для случая плоского движения твердого тела можно сразу указать такую ось, связанную с телом, относительно которой моменты сил инерции равны нулю и поэтому уравнение моментов имеет такой же вид, как и для осей, неподвижных в пространстве. Именно таким свойством обладает ось движущаяся поступательно и проходящая через центр масс тела. Тогда угловая скорость вра­щения всегда будет направлена вдоль этой оси.

Необходимо принимать во внимание лишь момент импульса отно­сительно этой оси вращения.

Уравнения движения маятника (1) и (2) относительно оси проходящей через центр масс перпендикулярно плоскости чертежа (рис. 1), имеют вид:

(3)

(4)

где - масса маятника с кольцом

(5)

где - масса оси, - масса диска и - масса кольца, одетого на диск.

- момент инерции маятника относительно оси, проходящей через центр масс.

- сила натяжения нитей.

-радиус оси кольца с намотанной нитью, т.е.

(6)

где - радиус оси, - диаметр нити подвеса.

Т.к. маятник движется с постоянным ускорением , то

(7)

где - высота, с которой опустился маятник,

- время опускания маятника. Решая совместно уравнения (3) - (7) получим

или (8)

где

Проверка точности измерения производится на основании определения рабочей погрешности определения момента инерции. Эта погрешность определяется по формуле:

(9)

где - измеренный момент инерции

- теоретическое значение момента инерции относительно той же оси что и .

определяется по формуле:

(10)

где - момент инерции оси маятника,

- момент инерции диска,

- момент инерции кольца.

Значения отдельных моментов инерции определяется по формулам:

(11)

где - диаметр оси маятника;

(12)

где - диаметр диска;

(13)

где - внешний диаметр кольца.

Погрешность не должна превышать 8%!

Эти данные можно использовать для проверки закона сохранения энергии. В начальный момент движения полная энергия маятника Максвелла равна его потенциальной энергия, т.е. где - масса маятника. В конечный момент (момент остановки секундомера) его энергия равна сумме кинетических энергий поступательного и вращательного движений, где - конечная скорость, - полный момент инерции, - конечная угловая скорость маятника, т.е. .

Тогда, согласно закону сохранения энергий:

или (14)

Для проверки точности метода вычисления определить величину:

, или

(15)

Т.к. движение маятника Максвелла равноускоренное, то

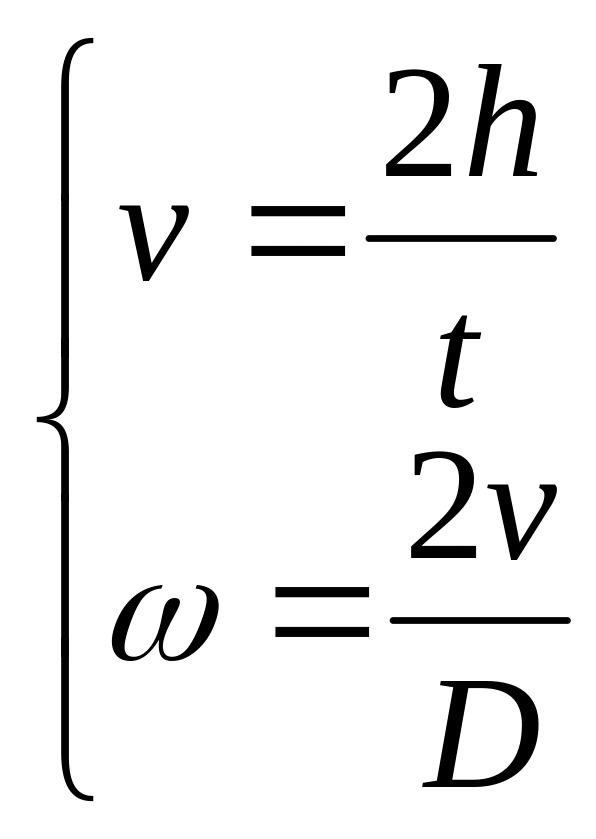(16)

При подстановке системы (16) в (15) и несложных преобразований получим рабочую формулу:

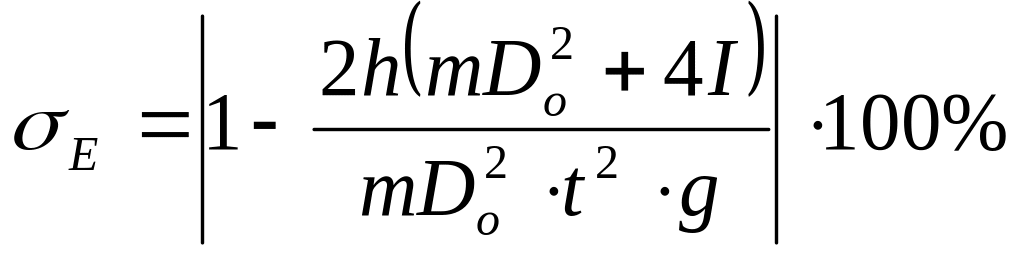(17)