
- •Часть 1
- •1.2. Классификация измерений
- •1.3. Основные характеристики измерений
- •1.4. Классификация средств измерений по роли,
- •1.5. Метрологические характеристики средств измерении и их нормирование. Классы точности
- •2.2. Оценивание и способы исключения систематических
- •2.3.1. Оценка случайных погрешностей при нормальном распределении результатов наблюдений
- •2.4. Суммирование погрешностей при прямых измерениях
- •2.5. Оценка погрешностей при косвенных измерениях
- •3. Формы представления результатов измерений и показатели точности
- •Содержание
3. Формы представления результатов измерений и показатели точности
Результат измерения представляется в виде значения величины и показателей точности. В зависимости от сложное? и ответственности измерений используются показатели точности измерения различной сложности.
При технических измерениях
физических величин, выполняемых
однократно, погрешность определяется
погрешностью средства измерения. Эта
погрешность известна до измерения из
нормативно-технической документации
к этому СИ. Записывается результат
измерения и погрешность в виде предела
до пускаемой суммарной погрешности.
Вероятность при этом не указывают,
предполагается, что ее значение
![]() = 0,997.
= 0,997.
При измерениях с многократными наблюдениями обработка их результатов проводится по-разному в зависимости от числа наблюдений, значимости систематических погрешностей, законов распределения случайных погрешностей и ряда других факторов.
Одним из установленных
показателей точности измерений является
интервал, в котором с установленной
вероятностью находится суммарная
погрешность измерения. Результаты
измерений должны быть представлены в
следующей форме:
;
![]() от
от
![]() до
до
![]() ;
,
где
- результат измерения в единицах
измеряемой величины (выборочное среднее),
,
;
,
где
- результат измерения в единицах
измеряемой величины (выборочное среднее),
,
![]() и
- соответственно погрешности измерения
с нижней и верхней её границами, в тех
же единицах,
- установленная вероятность, с которой
погрешность находится в этих границах,
Например, результат определения скорости
должен быть записан в такой форме: 121
м/с;
от - 1 до 2 м/с;
=0,99.
и
- соответственно погрешности измерения
с нижней и верхней её границами, в тех
же единицах,
- установленная вероятность, с которой
погрешность находится в этих границах,
Например, результат определения скорости
должен быть записан в такой форме: 121
м/с;
от - 1 до 2 м/с;
=0,99.
При симметричном (относительно результата измерений) интервале доверительной погрешности результата используется следующая форма записи:
![]() .
.
В простейшем случае, когда
выполнена одна серия наблюдений с
![]() и невозможно оценить и исключить
систематические погрешности,
ограничиваются вычислением среднего
арифметического результатов наблюдений
и оценки его среднего квадратического
отклонения по формуле (2,9). Результат
записывается в виде:
и невозможно оценить и исключить
систематические погрешности,
ограничиваются вычислением среднего
арифметического результатов наблюдений
и оценки его среднего квадратического
отклонения по формуле (2,9). Результат
записывается в виде:
![]()
Погрешность в окончательной записи принято выражать числом с одной или максимум двумя значащими цифрами. Две цифры удерживают при точном оценивании погрешностей, а также если цифра старшего разряда числа, выражающего погрешность, равна трем или меньше трех, например, 0,23,но 0,6. При приближенном оценивании погрешностей, когда погрешность выражают одной значащей цифрой, цифру 9 не применяют, а две значащие цифры сохраняют, если цифра старшего разряда меньше трех, при этом для младшего разряда обычно применяют только цифру 5. Например: 0,25; 0,15; 0,8; 1,0.
При промежуточных выкладках в числовых значениях погрешностей необходимо удерживать по три-четыре значащих цифры, чтобы погрешности округления значительно не искажали окончательный результат.
Числовое значение результата измерений должно быть представлено с учетом погрешности. Младший разряд результата должен соответствовать разряду погрешности.
Выбор способа, которым выражается точность измерений, и форма записи результата определяются назначением измерений и регламентируются соответствующими нормативно-техническими документами.
Кривые
 для разных значений
для разных значений
р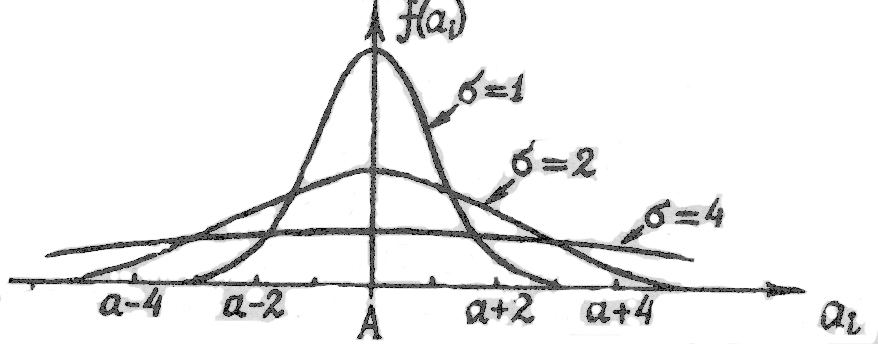 ис.2.1
ис.2.1
По оси абсцисс отложены единицы подходящим образом выбранного масштаба. Значение - в тех же местах.
Кривые
 для тех же значений
для тех же значений
р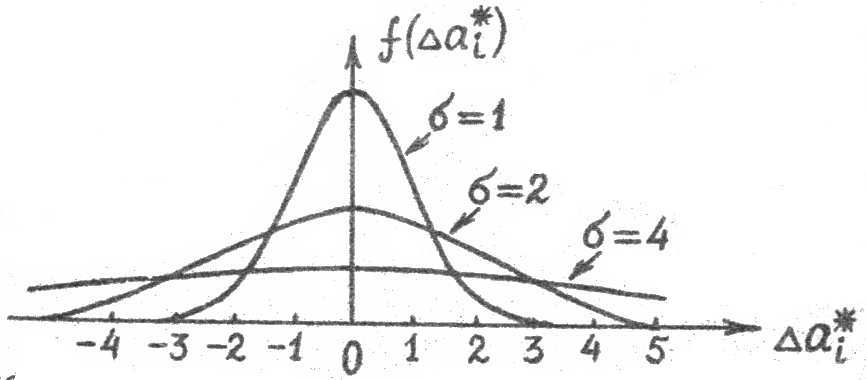 ис2.2
ис2.2
Взаимное расположение
истинного значения
и среднего значения
,
полученного из трех конкретных измерений
![]() и
.
и
.
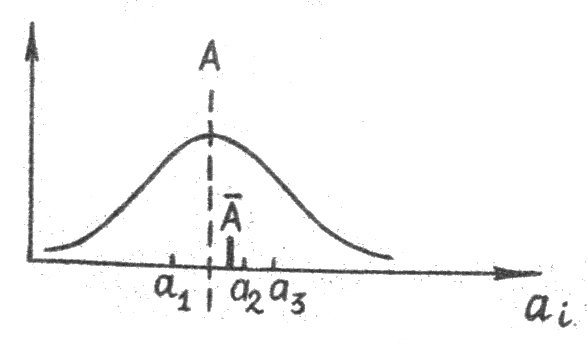
Рис2.3
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений. - М.: Наука, 1970.
2. Сквайрс Дж. Практическая физика. - М.: Мир, 1971.
3. Физический практикум: Механика и молекулярная физика/ Под ред. В.И. Ивероновой. - М.: Наука, 1967.
4. Зайдель А.Н. Элементарные оценки ошибок измерений. -М.: Наука, 1967.
5. Щиголев Б.М. Математическая обработка наблюдений. -М.: Физматгиз, 1962.
6. Гнеденко Б.В. Курс теории вероятностей. - М.: Наука, 1969.
7. Метрология, стандартизация и измерения в технике связи. -М.: Радио и связь, 1986.
8. ГОСТ 16263-70 Государственная система обеспечения единства измерений. Метрология. Термины и определения.
9. ГОСТ 8.009-84 Государственная система обеспечения единства измерений. Нормируемые метрологические характеристики средств измерений.
10. ГОСТ 8.207-76 Государственная система обеспечения единства измерений. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные, положения.
11. ГОСТ 8.401-80 Государственная система обеспечения единства измерений. Классы точности средств измерений. Общие требования.
