2.3.1. Оценка случайных погрешностей при нормальном распределении результатов наблюдений

Как показывает опыт, наиболее часто результаты реально­го физического эксперимента распределены по закону, называ­емому законом нормального распределения Гаусса (рис. 2. 1.);

(2.4.)

Эта функция задается двумя параметрами и ( - по­стоянная величина, называемая дисперсией распределения) и носит название функции Гаусса, а соответствующее распределе­ние называется гауссовым или нормальным распределением. От­метим, что плотность такого распределения симметрична отно­сительно , достигает максимального значения в точке и быстро стремится к нулю, когда становится большим по сравнению с .

Очевидно, что по своим свойствам такая функция вполне подходит для описания распределения результатов измерения при наличии только случайных погрешностей.

Аналогичным образом можно записать распределение дру­гой случайной величины - истинной погрешности (рис. 2. 2.):

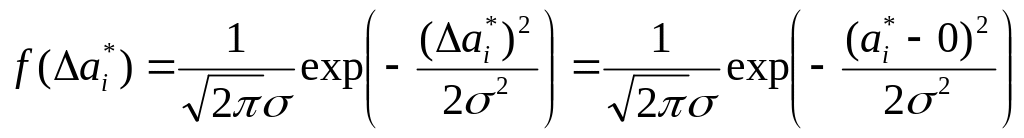
(2.5)

Индекс оставленный у , обозначает, что речь идет о распределении вероятностей появления погрешности отдельного измерения.

Нормальное распределение характеризуется двумя параметрами: 1) генеральным средним значением случайной величи­ны( ) и 2) дисперсией( ). Генеральное среднее значение представ­ляет собой то значение, относительно которого происходит разброс случайных величин. Так, например, в случае распреде­ления отдельных результатов измерений генеральным средним значением будет "истинное" значение (рис. 2.1.) В случае распределения истинных абсолютных погрешностей ; это ге­неральное среднее равно нулю (рис. 2.2.).

Дисперсия характеризует быстроту уменьшения вероят­ности появления погрешности с ростом величины этой по­грешности.

Под генеральной совокупностью подразумевается все мно­жество возможных значений измерений ; или возможных значе­ний погрешностей .

Остановимся несколько подробнее на связи между истинным значением измеряемой величины и средней величиной . На рис. 2.3. приведены в качестве частного примера положе­ния и , полученного из некоторых измеренных значений .

Мы видим, что даже при фиксированных значениях и различные значения , приводят к различному положению от­носительно . Так как вероятность появления разных значений различна, то и вероятность появления разных зна­чений также различна - с увеличением величины она уменьшается.

Таким образом, поскольку результаты отдельных измерений носят случайный характер, отклонение , т.е. вели­чина абсолютной погрешности результата серии измерений, также имеет случайный характер, так как оно зависит от вероятности появления того или иного значения .

При малом числе измерений величина отдельного изме­рения довольно сильно влияет на величину . Однако при большом числе измерений влияние величины отдельного изме­рения на величину становится значительно слабее, и от­клонение можно рассматривать как случайную величину, составленную из малых влияний величин отдельных измерений. В теории вероятностей доказывается, что распределение случай­ной величины описывается нормальным законом (2.5.) с другим значением дисперсии (связь между величинами и будет приведена ниже):

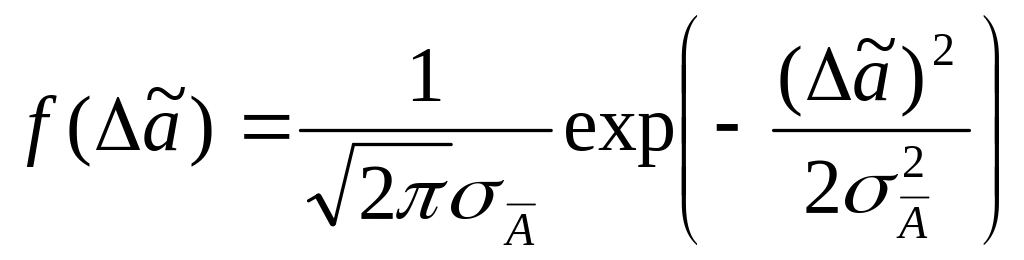
(2.6)

Вместо приближенного равенства можно записать: , или , но величина - оценка абсолютной погрешности результата - пока остается неопределенной. Следует различать - случайную величину (возможное значение ) и - частное значение этой ве­личины, проявившееся в данной серии измерений.

Назовем доверительным интервалом интервал , в который по определению попадает истинное значение изме­ряемой величины с заданной вероятностью. Надежностью или до­верительной вероятностью результата серии измерений называ­ется вероятность того, что истинное значение измеряе­мой величины попадает в данный доверительный интервал. Эта величина выражается в долях единицы или в процентах.

Чем больше величина доверительного интервала т.е. чем больше задаваемая погрешность результата измерений , тем с большей надежностью искомая величина попадает в этот интервал. Естественно, что величина надежности будет зависеть от числа произведенных измерений, а также от величины задаваемой погрешности . Так, например, при , выбирая равным значению , мы получаем сог­ласно закону (2.6.) величину надежности . Другими словами, за пределы доверительного интер­вала ( , ) при повторении серии по измере­ний попадает доля от числа всех серии, т.е. примерно в 32% всех серий будет больше .

Аналогично, выбирая равным значению , мы получа­ем значение надежности, равное , за пределы доверительного интервала вы­падает 5% результатов всех серий. Наконец, выбирая мы получим для надежности значение , т.е. за пределы доверительного интервала выпадает 0,3% результатов всех серий.

Перейдем теперь к рассмотрению - оценки погрешнос­ти результата серии намерений, остававшейся до сих пор неоп­ределенной.

Необходимо установить, как выражается величина через измеряемые величины .

В случае большого числа измерений величина дис­персии , входящая в закон (2.5.), оказывается равной так называемому среднему квадрату погрешности отдельного измере­ния :

.

Однако, как правило, точное значение искомой величины нам неизвестно, и поэтому погрешности не могут быть вы­числены. Вместо погрешностей находят обычно "измеряемые" абсолютные погрешности , равные . Все множество возможных значений распределено по закону, аналогичному (2.5.), и значение дисперсии о в этом законе совпадает со значением дисперсии в законе (2.5.).

При конечном числе измерений величина называется выборочным средним или средним выборки в отличие от гене­рального среднего, получающегося при . Выборка озна­чает, что из бесконечного множества (генеральной совокупнос­ти) возможных значений , берется наугад значений.

В случае, когда истинное значение неизвестно, оцен­кой дисперсии является так называемая выборочная диспер­сия или дисперсия выборки :

(2.8)

Подчеркнем, что при ограниченном числе величина является лишь оценкой дисперсии , а не равна ей, и, ис­ходя из результатов измерений, мы можем определить непосредственно лишь величину , а не ( при ).

Корень квадратный из выборочной дисперсии определяет так называемую среднеквадратичную погрешность отдельного из­мерения:

.

Теперь покажем, как найти оценку погрешности результата всей серии из измерений, т.е. величину , с заданным зна­чением надежности . Для этого найдем прежде всего, как связаны между собой и , т.е. дисперсии распределения погрешностей результата серии измерений и погрешностей отдельных измерений. В теории вероятностей показано, что дисперсия результата серии из измерений в раз меньшие дисперсии отдельных измерений, т.е. и ( - при большом числе серий).

Величину среднего квадратического отклонения - ре­зультата серии измерении можно оценить по следующей формуле:

(2.9) Оценки дисперсии и , полученные в (2.8.) и (2.9.), яв­ляются предельными, справедливыми лишь при , т.е. при большом числе измерений.

Для того, чтобы получить оценки границ доверительного интервала для в случае малых приходится ввести но­вый коэффициент . Зтот коэффициент был предложен в 1908 г. английским математиком и химиком B.C. Госсетом, пуб­ликовавшим свои работы под псевдонимом "Стьюдент" – студент, и получил впоследствии название коэффициента Стьюдента:

Коэффициент Стьюдента зависит от числа произведенных измерений и от величины надежности . Значения коэффициентов для разных значений надежности при разных значениях , приводятся обычно в виде таблицы.

Задавая вероятность того, что истинное значение измеря­емой величины попадает в данный доверительный интервал, т.е. другими словами, задавая надежность , равную определённой величине (например, ), мы можем по числу проведенных измерений (например, ) определить по таблице значение коэффициента Стьюдента для этих данных. Оно равно . Тогда, рассчитав предварительно по формуле (2.9.), найдем погрешность :

. (2.10.)

После этого результат измерений можно записать в виде , что означает, что истинное значение величины попадает в доверительный интервал ( ) с надежностью, равной .