
- •Пример вычисления дпф
- •Амплитудная и фазовая информация
- •B. Частотный интервал и симметрия дпф/бпф
- •Четное число выборок
- •Нечетное число выборок
- •Быстрое преобразование Фурье
- •Дополнение нулями
- •C. Спектр мощности
- •Экспресс-вп Измерения спектра
- •E. Характеристики различных типов спектральных и временных окон
- •Rectangular (Прямоугольное)
- •H. Идеальные фильтры
- •Влияние фильтров на частотное содержимое сигнала
- •I. Реальные (неидеальные) фильтры
- •Переходная полоса фильтра
- •Неравномерность полосы пропускания и ослабление в полосе режекции
- •J. Преимущества цифровых фильтров перед аналоговыми
- •K. Бих и ких фильтры
- •L. Бих фильтры
- •Реальные бих фильтры
- •Фильтры Баттерворта
- •Фильтры Чебышева
- •Фильтры Чебышева II типа или инверсные фильтры Чебышева
- •Эллиптические фильтры
- •Фильтры Бесселя
- •M. Сравнение бих фильтров
- •Примечания
C. Спектр мощности
ДПФ и БПФ действительного
сигнала являются комплексными числами,
имеющими действительную и мнимую части.
Мощность в каждой частотной компоненте
можно получить, возводя в квадрат
амплитуду этой компоненты. Следовательно,
мощность в k-ой
частотной компоненте (k-ый
элемент ДПФ/БПФ) выражается как |X[k]|2.
График, показывающий мощность каждой
частотной компоненты, называется
спектром мощности. Поскольку ДПФ/БПФ
действительного сигнала – симметрично,
то мощность на положительной частоте
kΔf
равна мощности на соответствующей
отрицательной частоте
–kΔf,
при этом постоянная компонента и
компонента на частоте Найквиста не
принимаются во внимание. Полная мощность
постоянной компоненты и компоненты на
частоте Найквиста равны
![]() и
и
 соответственно.
соответственно.
Потеря фазовой информации
Поскольку мощность получается возведением в квадрат амплитуды ДПФ/БПФ, спектр мощности всегда действителен, и всякая фазовая информация теряется. Чтобы выделить фазовую информацию, используйте ДПФ/БПФ, на выходе которых комплексные числа.
Спектр мощности можно использовать в тех приложениях, где фазовая информация не существенна, например, для вычисления спектра гармоник сигнала. Оно применяется для тестирования нелинейных систем, когда на их вход подают синусоидальный сигнал и смотрят мощность гармоник на выходе.
Частотный интервал между выборками
Частотный интервал между выборками равен Δf = fs/N. В следующей таблице спектр мощности сигнала x[n] обозначается как Sxx. Если N – четное, обозначим . В таблице показан формат выходной последовательности Sxx, соответствующей спектру мощности.
Элемент массива |
Интерпретация |
Sxx[0] |
Мощность постоянной компоненты |
Sxx[1] = Sxx[N–1] |
Мощность на частоте Δf |
Sxx[2] = Sxx[N–2] |
Мощность на частоте 2Δf |
Sxx[3] = Sxx[N–3] |
Мощность на частоте 3Δf |
. . . |
. . . |
Sxx[p–2] = Sxx[N–(p–2)] |
Мощность на частоте (p–2)Δf |
Sxx[p–1] = Sxx[N–(p–1)] |
Мощность на частоте (p–1)Δf |
Sxx[p] |
Мощность на частоте Найквиста |
Следующий рисунок наглядно представляет информацию из предыдущей таблицы для синусоидального сигнала с амплитудой 2 Vpeak (Vpk) и N = 8.
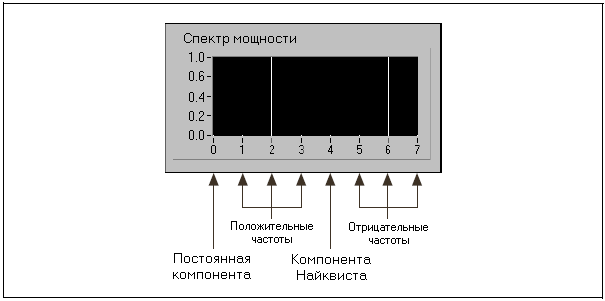
Спектр мощности вычисляется
в единицах среднеквадратичного
действующего напряжения в квадрате
(![]() ).
Так что если максимальная амплитуда
входного сигнала равна 2
Vpk,
то среднеквадратичное действующее
значение равно
).
Так что если максимальная амплитуда
входного сигнала равна 2
Vpk,
то среднеквадратичное действующее
значение равно
![]() ,
то есть
,
то есть
![]() .
В это значение вносят вклад поровну
положительные и отрицательные компоненты,
в результате получается график, показанный
на предыдущем рисунке.
.
В это значение вносят вклад поровну
положительные и отрицательные компоненты,
в результате получается график, показанный
на предыдущем рисунке.
Если N – нечетное, положим p = (N – 1)/2. Следующая таблица показывает формат выходной последовательности Sxx, соответствующей спектру мощности.
Элемент массива |
Интерпретация |
Sxx[0] |
Мощность постоянной компоненты |
Sxx[1] = Sxx[N–1] |
Мощность на частоте Δf |
Sxx[2] = Sxx[N–2] |
Мощность на частоте 2Δf |
Sxx[3] = Sxx[N–3] |
Мощность на частоте 3Δf |
. . . |
. . . |
Sxx[p–2] = Sxx[N–(p–2)] |
Мощность на частоте (p–2)Δf |
Sxx[p–1] = Sxx[N–(p–1)] |
Мощность на частоте (p–1)Δf |
Sxx[p] |
Мощность на частоте pΔf |
Следующий рисунок иллюстрирует информацию предыдущей таблицы для N = 7.

