1. Определить основные параметры для линейного корректирующего кода (9,4)

Основные параметры линейного корректирующего кода (9,4):

1. Основание кода q – число элементарных символов, выбранных для передачи сообщения: q ={0;1}

2. Длина кода n = 9 – число символов, выбранных для передачи сообщения.

3. Число информационных позиций в коде, выбранных для передачи данных k = 4.

4. Число проверочных позиций в коде r = n – k = 9 – 4 = 5.

5. Скорость передачи кода:

6. Кодовое расстояние кода d = 3 – наименьшее расстояние Хэмминга (число позиций, в которых кодовые слова отличаются друг от друга) между различными парами кодовых слов.

7. Кратность контролируемой ошибки t.

7.1. Кратность обнаружения ошибки:

То есть данный код позволяет обнаружить не более двух ошибок.

7.2. Кратность коррекции ошибки:

Значение кратности коррекции ошибки t_к = 1, то есть данный код позволяет корректировать одну ошибку.

2. Записать порождающую и проверочную матрицы для кода (7,4), указав на способ получения проверочных символов

Код Хэминнга является линейным блочным кодом, для описания которых удобно пользоваться порождаюшей матрицей.

Запишем порождающую матрицу G. Матрица G будет иметь размерность . В качестве строк матрицы G выбираем любые линейно-независимые слова, отстоящие друг от друга на кодовое расстояние равное 3:

Пусть входное слово имеет вид:

Выходное слово получаем умножением входного слова на порождающую матрицу: . В результате получим выходное слово:

,

где

(1)

То есть 4 крайних левых символов кодового слова совпадают с символами кодируемой информационной последовательности, остальные 3 – являются линейными комбинациями символами информационной последовательности.

Линейные коды кроме порождающей матрицы задаются также и проверочной матрицей. Эти матрицы связаны между собой соотношением . Поверочная матрица будет иметь размерность , где . Приведем проверочную матрицу в виде

3. Закодировать сообщения 0011, 1000 линейным корректирующим кодом (7,4). Нарисовать структурную схему кодирующего устройства и описать алгоритм его работы

Закодируем сообщение 0011

Закодируем сообщение 1000

На основании порождающей матрицы или приведенной выше системы проверочных уравнений (1) составим структурную схему кодера (рис. 1):

Рисунок 1

Кодер работает как схема при простой проверке на четность, причем делает несколько проверок, формируя соответственно, несколько проверочных символов. Если число единиц в последовательности m четно, то результатом суммирования будет 0, если нечетно – 1, что и показывают проверочные уравнения (1).

4. Декодировать сообщения 0011101 и 1000101 синдромным методом (указав на возможные ошибки при декодировании). Нарисовать структурную схему декодирующего устройства и описать алгоритм его работы

Допустим в канале передачи на вектор кодовой последовательности накладывается вектор ошибки , представляющий собой вектор длиной n = 7 с единицами в тех позициях, где присутствует ошибка. Соответственно, принятая комбинация будет иметь вид:

Приняв вектор декодер должен сначала определить, имеются ли в принятой последовательности ошибки. Если ошибки есть, он (декодер) должен выполнить действия по исправлению.

Чтобы выяснить является ли принятая последовательность кодовым словом декодер вычисляет синдром, определяемый следующим образом:

Пусть принятый вектор , тогда:

(2)

Если синдром , следовательно, в принятой кодовой последовательности имеются ошибки.

В нашем случае для принятой комбинации 0011101:

, следовательно, в принятой комбинации есть ошибка

В нашем случае для принятой комбинации 1000101:

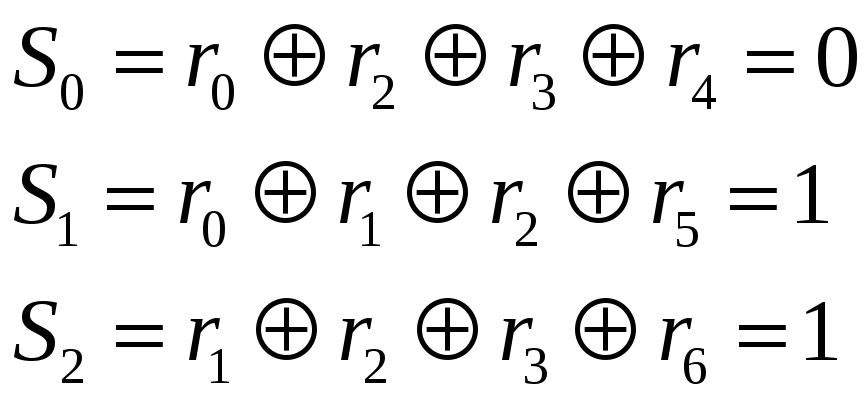
, следовательно, в принятой комбинации есть ошибка

Используем полученный синдром для исправления ошибки. Выше мы условились, что передаваемый вектор: ; вектор ошибки:; вектор принятый – и . Тогда

, то есть синдром зависит только от ошибки, имеющейся в принятой последовательности. Тогда найдя вектор ошибки, восстановим кодовое слово:

Как мы заметили выше синдром будет однозначно определяться вектором ошибки, следовательно, необходимо найти значения синдрома для всех возможных ошибок

…

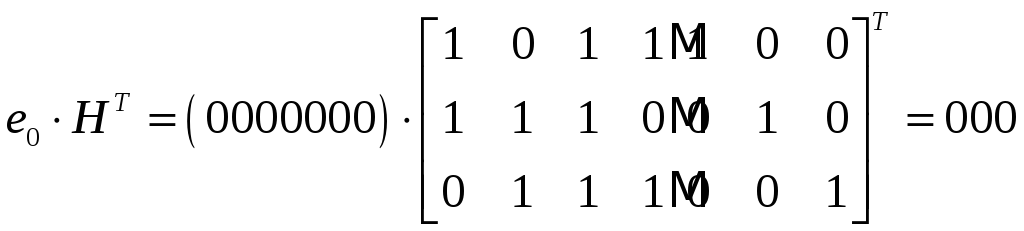
и т.д.

То есть синдромами будут строки матрицы Н. Таким образом, запишем все возможные ошибки и соответствующие им синдромы в виде таблицы:

Номер символа, в котором ошибка	Вектор ошибки	Синдром ошибки S1S2S3S4	Десятичный код синдрома
1	1000000	110	6
2	0100000	011	3
3	0010000	111	7
4	0001000	101	5
5	0000100	100	4
6	0000010	010	2
7	0000001	001	1

Из этой таблицы видно, что существует однозначное соответствие между сочетанием ошибок (при одиночной ошибке) и его синдромом, то есть, зная синдром, можно совершенно однозначно определить позицию кода, в котором произошла ошибка.

Полученный первый синдром S = 111, говорит об ошибке в третьем символе. Однако, если сравнить принятую комбинации 0011101 с закодированным сообщением 0011010, то видно, что имеются три ошибки.

Аналогично при сравнении принятой комбинации 1000101 с закодированным сообщением 1000110, то видно, что имеются две ошибки, хотя синдром показывает ошибку в втором символе.

Эти результаты объясняются тем, что код (7,4) (код Хэмминга) имеет кодовое расстояние равное 3 и позволяет обнаружить 2 ошибки и исправить 1 ошибку.

Основываясь на соотношениях (2) построим структурную схему декодирующего устройства (рис. 2):

Рисунок 2

Принцип работа декодирующего устройства прост: в соответствии с соотношениями (2) вычисляется суммирование по модулю 2 определенных позиции принятой комбинации.

Список использованной литературы

1. Теория прикладного кодирования: Учебное пособие в 2х т. Т.2; Под ред. проф. В.К. Конопелько. – Мн.: БГУИР, 2004 – 398с.

2. Богданович М.И. Цифровые интегральные микросхемы. Справочник. – Мн.: Беларусь, 1996. – 605с.

3. Хэмминг Р.В. Теория кодирования и теория информации. – М.: Радио и связь, 1987 г.

10