
контрольная ММвЦОС 4ый вариант
.docxКонтрольное задание №4
1
Показать, что дискретная система,
описываемая уравнением
 является нелинейной.
является нелинейной.
Решение:
Систему называют линейной, если она обладает свойствами:
- аддитивности: реакция на сумму воздействий равна сумме реакций на каждое из воздействий (принцип суперпозиции);
- однородности: умножению воздействия на весовой коэффициент соответствует реакция, умноженная на тот же коэффициент.
Соотношение вход/выход линейной системы описывается линейным уравнением.
Следовательно,
система, описанная уравнением уравнением
 ,
является нелинейной.
,
является нелинейной.
2
Вычислить линейную свертку двух
дискретных последовательностей, где
 импульсная характеристика цифровой
системы,
импульсная характеристика цифровой
системы,
 реакция
системы на входную последовательность
реакция
системы на входную последовательность
 .
Построить график свертки.
.
Построить график свертки.
Решение:
















3
Показать, что разностное уравнение
 c
начальным условием
c
начальным условием
 },
где
},
где
 входная последовательность, описывает
отклик cумматора
входная последовательность, описывает
отклик cумматора .
.
Решение:





Следовательно,

4
Вычислить Фурье-образ (дискретизированное
по времени преобразование Фурье)
последовательности
где Построить
графики модуля и фазы как функции
нормированной частоты
Построить
графики модуля и фазы как функции
нормированной частоты
 в
диапазоне
в
диапазоне
 где
где
 ,
,
 –
циклическая и линейная частоты,
–
циклическая и линейная частоты,
 -
частота дискретизации.
-
частота дискретизации.
Решение:
Исходная последовательность
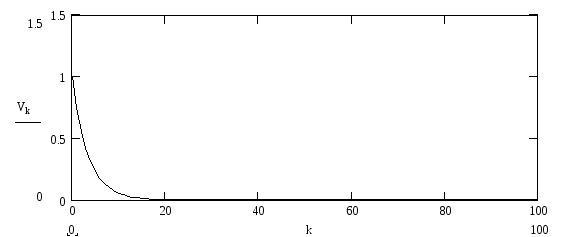
График модуля

График фазы

5
Вычислить элементы системы дискретных
экспоненциальных функций (ДЭФ) и записать
систему в виде матрицы размером
размером
 Матрицу представить в алгебраической
и экспоненциальной форме.
Матрицу представить в алгебраической
и экспоненциальной форме.
Решение:
В дискретном преобразовании Фурье используется система дискретных экспоненциальных функций (ДЭФ), определяемых следующим выражением

Обе
переменные
 принимают дискретные значении
принимают дискретные значении

Обозначим
Тогда

Всю
систему ДЭФ можно записать в виде матрицы
V , строки которой нумеруются переменной
k
, столбцы
переменной п,
а
в пересечении k-n
строки
и n-го столбца записана величина



Рисунок 2 – Поворачивающие множители ДПФ
Для N=3 матрица V имеет вид:

6
Выполнить прямое дискретное преобразование
Фурье (ДПФ) последовательности
 Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье
Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье .
.
Решение:
 ,
k=0,1,…,N-1;
,
k=0,1,…,N-1;
 ,
n=0,1,…,N-1.
,
n=0,1,…,N-1.
Выражение
для вычисления
 называется прямым преобразованием
(ДПФ), а для вычисления
называется прямым преобразованием
(ДПФ), а для вычисления
 - обратным (ОДПФ).
- обратным (ОДПФ).
Коэффициент
 (постоянная составляющая) равен сумме
всех отсчетных значений сигнала:
(постоянная составляющая) равен сумме
всех отсчетных значений сигнала:





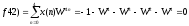








7
Дана последовательность
 Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
 по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
Решение:
Сигнал состоит из 8-х отсчетов во временной области. Применяя уравнение ДПФ, получаем:

Разобьем эту сумму на две при n = (0, 2, 4, 6) и (1, 3, 5, 7). Получим выражение:

Раскрывая суммы, запишем

Два различных поворачивающих множителя можно связать с помощью определения:

Тогда формула примет вид:

Полученное выражение для 8-точечного БПФ не слишком сложно, но по мере возрастания количества точек увеличивается его сложность. Чтобы упростить выражение, его обычно изображают в другом виде.
Представим
в виде графа алгоритм БПФ с прореживанием
по времени основанный на разбиении —
объединении при ![]()
 Рисунок
- Граф алгоритма БПФ с прореживанием по
времени при N=8
Рисунок
- Граф алгоритма БПФ с прореживанием по
времени при N=8
На
первом этапе отсчеты входного сигнала
переставляются местами и исходная
последовательность делится на «четную»
и «нечетную последовательности»
(обозначены красными и синими стрелками).
Потом «четная» и «нечетная»
последовательности в свою очередь
делятся на «четную» и «нечетную»
последовательности. При ![]() такое
деление можно делать
такое
деление можно делать ![]() раз.
В нашем случае
раз.
В нашем случае ![]() .
Данная процедура называется
двоично-инверсной перестановкой, так
можно выполнить перенумерацию отсчетов
переписав номер отсчета в двоичной
системе в обратном направлении.
Например
.
Данная процедура называется
двоично-инверсной перестановкой, так
можно выполнить перенумерацию отсчетов
переписав номер отсчета в двоичной
системе в обратном направлении.
Например ![]() имеет
индекс в десятичной системе счисления
имеет
индекс в десятичной системе счисления ![]() ,
если же
,
если же ![]() переписать
справа налево то получим
переписать
справа налево то получим ![]() ,
то есть
,
то есть ![]() после
разбиения на четные нечетные перед
первой операцией «Бабочка» встанет на
место
после
разбиения на четные нечетные перед
первой операцией «Бабочка» встанет на
место ![]() ,
которая в свою очередь встанет на
место
,
которая в свою очередь встанет на
место ![]() .
По аналогичному правилу поменяются
местами все отсчеты, при этом некоторые
останутся на месте, в частности
.
По аналогичному правилу поменяются
местами все отсчеты, при этом некоторые
останутся на месте, в частности![]() ,
так как если
,
так как если ![]() переписать
справа налево то все равно останется
переписать
справа налево то все равно останется ![]() ,
аналогично
,
аналогично ![]()
![]() и
и![]() .
Очень важно понять, что данный метод
перенумерации должен применяться при
записи числа в двоичной системе состоящей
из
.
Очень важно понять, что данный метод
перенумерации должен применяться при
записи числа в двоичной системе состоящей
из ![]() разрядов.
В приведенном примере использовалось
3 разряда двоичного числа, но если
же
разрядов.
В приведенном примере использовалось
3 разряда двоичного числа, но если
же ![]() (
(![]() ),
то необходимо записать число при
использовании 4 разрядов. В этом случае
),
то необходимо записать число при
использовании 4 разрядов. В этом случае ![]() и
после переписывания получим
и
после переписывания получим ![]() ,
то есть при
,
то есть при ![]()
![]() не
останется на месте, а поменяется местами
с
не
останется на месте, а поменяется местами
с ![]() .
.
Можно
сказать что напрямую двоично-инверсная
перестановка удобна когда заранее
количество отсчетов входного сигнала
фиксировано, однако в универсальных
алгоритмах БПФ на различные размеры ![]() ,
двоично-инверсная перестановка не
эффективна, проще и быстрее поменять
отсчеты местами.
,
двоично-инверсная перестановка не
эффективна, проще и быстрее поменять
отсчеты местами.
После двоично-инверсной перестановки получаем четыре 2-точечных ДПФ:
|
|
|
На основе четырех 2-точечных ДПФ формируются два 4-точечных ДПФ:
|
|
|
И на последнем уровне формируется полный спектр входного сигнала.

Алгоритм
с прореживанием по времени на каждом
уровне требует ![]() комплексных
умножений и сложений. При
комплексных
умножений и сложений. При ![]() количество
уровней разложения — объединения
равно
количество
уровней разложения — объединения
равно ![]() ,
таким образом общее количество операций
умножения и сложения равно
,
таким образом общее количество операций
умножения и сложения равно ![]() .
.
8
Заданы последовательности
 и
и Вычислить
циклическую дискретную свертку
последовательностей с помощью ДПФ.
Построить график свертки.
Вычислить
циклическую дискретную свертку
последовательностей с помощью ДПФ.
Построить график свертки.
Использование БПФ для вычисления свертки основано на том, что ДПФ свертки последовательностей есть покомпонентное произведение ДПФ соответствующих последовательностей.
Для выполнения свертки с помощью дискретного преобразования Фурье необходимо дополнить нулями обе входные последовательности так, чтобы количество элементов в этих последовательностях равнялось Nвых=4+5-1=8. Далее необходимо произвести прямое ДПФ по формуле прямого преобразования Фурье.
Вычислим ДПФ последовательностей:
 ,
k=0,1,…,7;
,
k=0,1,…,7;




Далее производится поочередное умножение элементов первой последовательности с элементами второй последовательности и просуммировать полученные значения. После производится обратное преобразование по формуле обратного преобразования, в результате которого получаем свертку, рассчитанную с помощью ДПФ.

 ,
n=0,1,…,7.
,
n=0,1,…,7.


9
Вычислить матрицу косинусных функций
дискретного косинусного преобразования
(ДКП) размером
 Матрицу представить в алгебраической
и экспоненциальной форме.
Матрицу представить в алгебраической
и экспоненциальной форме.
Решение:


10
Выполнить прямое ДКП последовательности
последовательности
 Изобразить
график функции
Изобразить
график функции .
Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
.
Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
 .
.
Решение:




11Вычислить
двумерное ДКП массива данных
 размером
размером
 Восстановить исходный массив, выполнив
двумерноеобратное дискретное косинусное
преобразование (ОДКП), если
Восстановить исходный массив, выполнив
двумерноеобратное дискретное косинусное
преобразование (ОДКП), если
Решение:
Матрица
ДКП
 :
:

Двумерное
ДКП массива данных


Обратное ДКП:

12Вычислить среднеквадратичную ошибку восстановления исходных данных (задача 11) при обнулении 12,5 % наименьших по значениям коэффициентов преобразования ДКП и последующем выполнении ОДКП над полученным массивом.
Решение:
Обнулим 12 наименьших значений матрицы с·х:

Обратное ДКП

Среднеквадратичная ошибка восстановления исходных данных:



