
Сложение коллинеарных скользящих векторов
Если
скользящие векторы параллельны, то при
их сложении главная трудность состоит
в определении прямой, на которой будет
расположена их сумма. (Величину и
направление вектора суммы было бы
естественно определить точно так же,
как и в случае сложения свободных
векторов.) В механике
при изучении статики
для решения вопроса о сложении параллельных
сил, которые, как известно, задаются
скользящими векторами, вводится
дополнительная гипотеза: к системе
векторов можно добавить два вектора,
равных по величине, противоположных по
направлению и расположенных на одной
прямой, пересекающей прямые, на которых
расположены данные вектора. Пусть,
например, надо сложить скользящие
векторы
![]() и
и
![]() ,
расположенные на параллельных прямых.
Добавим к ним векторы
,
расположенные на параллельных прямых.
Добавим к ним векторы
![]() и
и
![]() ,
расположенные на одной прямой. Прямые,
на которых расположены векторы
и
,
и
пересекаются.
Поэтому определены векторы
,
расположенные на одной прямой. Прямые,
на которых расположены векторы
и
,
и
пересекаются.
Поэтому определены векторы
![]()
Прямые,
на которых расположены векторы
![]() и
и
![]() ,
пересекаются всегда, за исключением
случая, когда векторы
и
равны
по величине и противоположны по
направлению, в котором говорят, что
векторы
и
,
пересекаются всегда, за исключением
случая, когда векторы
и
равны
по величине и противоположны по
направлению, в котором говорят, что
векторы
и
![]() образуют
пару
(векторов).
образуют
пару
(векторов).
Таким образом, под суммой векторов и можно понимать сумму векторов и , и эта сумма векторов определена корректно во всех случаях, когда векторы и не образуют пару.
Произведение вектора на число
Произведением
вектора
и
числа λ называется вектор, обозначаемый
![]() (или
(или
![]() ),
модуль которого равен
),
модуль которого равен
![]() ,
а направление совпадает с направлением
вектора
,
если
,
а направление совпадает с направлением
вектора
,
если
![]() ,
и противоположно ему, если
,
и противоположно ему, если
![]() .
Если же
.
Если же
![]() ,
или вектор
нулевой,
тогда и только тогда произведение
—
нулевой вектор.
,
или вектор
нулевой,
тогда и только тогда произведение
—
нулевой вектор.
Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе,
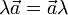 .
.
Из определения произведения вектора на число легко вывести следующие свойства:
если
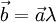 ,
то
,
то
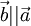 .
Наоборот, если
.
Наоборот, если
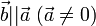 ,
то при некотором λ верно равенство
;
,
то при некотором λ верно равенство
;всегда
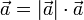 °,
то есть каждый вектор равен произведению
его модуля на орт.
°,
то есть каждый вектор равен произведению
его модуля на орт.
Скалярное произведение
Скалярным
произведением векторов
и
называют
число, равное
![]() ,
где
,
где
![]() —
угол
между векторами
и
—
угол
между векторами
и
![]() .
Обозначения:
.
Обозначения:
![]() или
или
![]() .
.
Если один из векторов является нулевым, то несмотря на то, что угол не определён, произведение равно нулю.
Свойства скалярного произведения векторов:
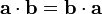 —
коммутативность.
—
коммутативность.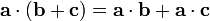 —
дистрибутивность.
—
дистрибутивность.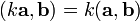 —
линейность
по отношению к умножению на число.
—
линейность
по отношению к умножению на число.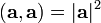 —
норма
вектора
(Квадрат вектора).
—
норма
вектора
(Квадрат вектора).
Геометрически скалярное произведение есть произведение длины одного из сомножителей на ортогональную проекцию другого на направление первого (или наоборот). Скалярное произведение какого-то вектора с единичным вектором есть ортогональная проекция вектора на направление единичного вектора.
Векторное произведение
Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям:
длина вектора c равна произведению длин векторов a и b на синус угла φ между ними
![]()
вектор c ортогонален каждому из векторов a и b
вектор c направлен так, что тройка векторов abc является правой.
Обозначение:
![]()
Геометрически
векторное произведение
![]() есть
ориентированная площадь
параллелограмма,
построенного на векторах
есть
ориентированная площадь
параллелограмма,
построенного на векторах
![]() ,
представленная псевдовектором,
ортогональным этому параллелограмму.
,
представленная псевдовектором,
ортогональным этому параллелограмму.
Свойства векторного произведения:
При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е
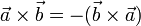
Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть
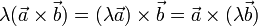
Векторное произведение обладает распределительным свойством:
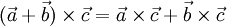
Смешанное произведение
Сме́шанное
произведе́ние
![]() векторов
векторов
![]() —
скалярное
произведение
вектора
на
векторное
произведение
векторов
и
:
—
скалярное
произведение
вектора
на
векторное
произведение
векторов
и
:
![]()
(равенство записано для разных обозначений скалярного и векторного произведения).
Иногда смешанное произведение называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрически смешанное произведение есть (ориентированный) объём параллелепипеда, построенного на векторах .
История
Интуитивно вектор понимается как объект, имеющий величину, направление и (необязательно) точку приложения. Зачатки векторного исчисления появились вместе с геометрической моделью комплексных чисел (Гаусс, 1831). Развитые операции с векторами опубликовал Гамильтон как часть своего кватернионного исчисления (вектор образовывали мнимые компоненты кватерниона). Гамильтон предложил сам термин вектор (лат. vector, несущий) и описал некоторые операции векторного анализа. Этот формализм использовал Максвелл в своих трудах по электромагнетизму, тем самым обратив внимание учёных на новое исчисление. Вскоре вышли «Элементы векторного анализа» Гиббса (1880-е годы), а затем Хевисайд (1903) придал векторному анализу современный вид
