4.3. Абсолютна похибка виміру температури оточуючого повітря

Межа допустимої основної похибки виміру температури оточуючого повітря t_в у відповідності до табл…… складає

Δt_в = ± 0,2 °С (додаток.)

Або у відносних одиницях

4.4. Абсолютна похибка виміру площі поверхні трубки

Абсолютна похибка (або допустиме відхилення) виміру діаметра трубки штангенциркулем складає Δd = ± 0,01 мм (0,00001м) що відповідає ціні поділу, а довжини Δl = ± 0,5 мм (0,0005 м).

Абсолютна похибка визначення площі поверхні трубки визначається за формулою і складе

Δ F = ± = ± =

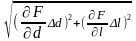= ± 1,57·10^-4 м².

4.5. Абсолютна похибка виміру теплового потоку

У відповідності до формули (3.1) тепловий потік Q є результатом прямих вимірів сили струму I, А в ланцюгу та непрямих вимірів електричного опору R_t , Ом трубки. Тобто складовими абсолютної похибки теплового потоку ΔQ є абсолютні похибки сили струму ΔI та електричного опору трубки ΔR.

4.5.1. Визначення похибки виміру електричного опору

Похибка в визначенні опору трубки ΔR складається з похибки приладу для виміру опору ΔR_п та похибки виміру температури стінки трубки ΔR_т.

Складова ΔR_п визначається із умов задачі як ± 0,2% (клас точності 0,2) від отриманого значення опору, що дорівнює 0,5 Ом і становить

ΔR_п = ± Ч 0,5 = ± 0,001 Ом.

Складова похибки виміру опору трубки за рахунок виміру температури складає

ΔR_т = ± R_{0 ´} б ´ Δt_с = 0,5 ´ 4 ´ 10^-3 ´ 2,9 = ± 0,0058 Ом.

Межа сумарної допустимої похибки визначення опору трубки по значенню її температури при умові, що обидві похибки ΔR_т та ΔR_п - є незалежними одна від другої, складе

ΔR = ± 0,0059 Ом.

або у відносних одиницях

ΔR / R = ± 0,0059 / 0,9 = ± 0,0066.

4.5.2. Абсолютна похибка визначення теплового потоку

Тепер можна оцінити похибку визначення теплового потоку за формулою

ΔQ = ± = ± = ± 0,39 Вт.

Отримані значення фізичних величин та їх похибки занесено до таблиці.

Результати вимірів фізичних величин та їх абсолютних похибок Таблиця 4.1.

№ п/п	Фізична величина	Значення фізичної величини та абсолютної похибки	Значення відносної похибки, %
1	Тепловий потік, Q складові: сила струму, I електричний опір трубки, R	18,54 ± 0,39 Вт 4,2 ± 0,05 А 0,9 ± 0,0059 Ом	± 0,02 ± 0,12 ± 0,66
2	Площа поверхні трубки, F	0,00314 ± 1,57·10-4 м2	± 5,0
3	Температура стінки трубки, tс	200 ± 2,9 °С	± 1,45
4	Температура оточуючого повітря, tв	20 ± 0,2 °С	± 1,0

5. Визначення похибки виміру коефіцієнта тепловіддачі

Маючи значення допустимих похибок кожного аргументу, можна перейти до підрахунку границь похибки визначення коефіцієнта теплопередачі за формулою (2.2). Спочатку визначаються часткові похідні кожної складової похибки:

;

;

;

.

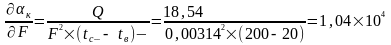
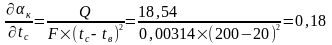
Нарешті абсолютна похибка

Δ ( ) = ± =

= ±1,85 .

Розрахункове значення коефіцієнта тепловіддачі складе

= = .

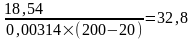Границя допустимої відносної похибки

∆ = = ± = ± 5,64 %.

Отримане значення межі допустимої похибки перевищує потрібне на величину 5,64 – 5 = 0,64%, тому треба проаналізувати кожну складову загальної похибки, оцінити їх внески, скорегувати точність визначення окремих аргументів і зменшити загальну похибку до потрібної величини 5%.

Значення складових похибки Таблиця 5.1

Найменування складових похибок	Значення складовоі	Частка складових похибки /∑ , %
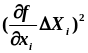За рахунок визначення теплового потоку, ΔQ, Вт	0,476	13,93
За рахунок визначення площі поверхні трубки, Δ F, м2	2,666	78,05
За рахунок визначення темпера-тури стінки трубки, Δtc, °С	0,272	7,98
За рахунок визначення температури повітря, Δtв, °С	0,0013	0,04

∑ = 3,42 ∑ = 100

Аналіз кожної складової похибки показує, що найбільший внесок в похибку вносять складові за рахунок визначення площи поверхні трубки ΔF = 78,05 % та за рахунок визначення теплового потоку трубки ΔQ = 13,93 %. Зменшити похибку ми можемо тільки за рахунок заміни термопари на більш точну.

Аналізуємо складову під коренем в формулі (2.2), де значення часткової похідної - множник - становить 1,04·10⁴ , що значно більше множника ΔF = 1,57·10^-4. Значення часткової похідної не може бути скореговане тому, що ця величина є коефіцієнтом впливу і характеризує “участь” власно площі поверхні в загальній похибці. А от значення абсолютної похибки вимірів ΔF теоретично можна зменшити за рахунок підвищення точності вимірювальних інструментів. Однак точність виміру діаметру трубки складає ± 0,1%, а довжини - ± 0,05%, що є достатньо високими значеннями, тому подальше її підвищення не буде раціональним.

В похибці визначення теплового потоку трубки Δt_c, головною складовою є похибка термоелектричного термометра, абсолютне значення якої складає ± 2,9 °С, а відносне - ± 100 % = ± 1,45 %. Цю величину можна зменшити. За додатком [1] підбираємо більш точний термоелектричний термометр ПП(S) зі шкалою 0…300 °С, з максимальним допустимим абсолютним відхиленням термо-ЕРС від номінального значення ± 0,008 мВ (табл. 2 дод.). За табл. № 1 додатка шляхом інтерполяції Δt_c=1,441 °С, тоді складова похибки Δ ( ) за рахунок t_c буде

= (0,18 ´ 1,441)² = 0,067 , (було 0,272)

скорегуємо також складову похибки виміру електричного опору трубки, тому що вона фігурує в розрахунках (див. …)

ΔR_т = ± R_{0 ´}б ´ Δt = 0,5 ´ 4 ´ 10^-3 ´ 1,441 = ± 0,0029 Ом, вона, як бачимо, зменшилась на 0,0059 – 0,0029 = 0,003 Ом, а загальна похибка виміру опору складе

ΔR = ± 0,00307 Ом

у відповідності до корекції похибки визначення електричного опору трубки ΔR, похибка визначення потужності складе

_ΔQ = ± = ± = ± 0,38 Вт

(а було ΔQ = ± 39 Вт), а скореговане значення похибки у визначенні коефіцієнта тепловіддачі складе

Δ( ) = ± = ± 1,79 , або у відносних одиницях

Δ ( )_В = ± = ± 5,46 %, що задовольняє умовам завдання.

Запишемо результат у вигляді довірчого інтервалу в межах визначеної похибки

α_к = 32,8 ± 1,79 .