
- •©СПбГэту«лэти», 2003 Введение
- •Занятие 1. Кинематика
- •1.1. Подготовительное задание
- •1.2. Теоретическое задание
- •1.3. Индивидуальное задание
- •1.4. Контрольные задания
- •2.1. Подготовительное занятие
- •2.2.Теоретическое задание
- •2.3.Индивидуальное задание
- •2.4. Контрольное задание
- •3.1. Подготовительное задание
- •3.2. Теоретическое задание
- •3.3. Индивидуальное задание.
- •3.4. Контрольное задание.
- •4.1.Подготовительное задание
- •4.2. Теоретическое занятие.
- •4.3.Индивидуальное задание.
- •4.4.Контрольное задание
- •Список рекомендуемой литературы
- •Содержание
- •197376, С.-Петербург, ул. Проф. Попова, 5
2.4. Контрольное задание
2.4.1. Концы невесомой нерастяжимой нити намотаны на два однородных сплошных диска, один из которых имеет фиксированную ось вращения (рис.2.4а). Второй диск, вращаясь, движется вниз. Найдите ускорение центра масс второго диска.
Ответ : 7,8 м/c2 .
2.4.2. На сплошной однородный диск с фиксированной осью вращения намотана невесомая нерастяжимая нить (рис.2.4б).. К концу нити прикреплен груз массой 2 кг. Груз движется вниз, разматывая нить. Найдите ускорение груза, если масса груза 3 кг.
Ответ : 5,6 м/c2
2.4.3. Через сплошной однородный диск с фиксированной осью вращения (рис.2.4в) перекинута невесомая нерастяжимая нить. К концам нити прикреплены грузы массами 2 кг и 3 кг, которые при своем движении заставляют диск вращаться без проскальзывания. Найдите ускорение грузов, если масса диска 3 кг.
Ответ: 2.8 м/с2.
-

a)

б)

в)

г)
рис. 2.4.
2.4.4. На сплошной однородный диск намотана невесомая нерастяжимая нить, второй конец которой закреплен (рис.2.4г). С каким ускорением будет опускаться диск, если его предоставить самому себе?
Ответ : 6,5 м/c2
2.4.5. Вентилятор вращается с частотой n = 15 с-1. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 оборотов. Работа сил торможения А = 44,4 Дж. Определите момент сил торможения, считая его постоянным.
Ответ: 94 10-3 Н м.
Занятие 3. ЗАКОНЫ СОХРАНЕНИЯ
3.1. Подготовительное задание
3.1.1. Дайте определение частной производной функции. Какой геометрический смысл имеет частная производная от функции двух переменных? Как вычислить значение частной производной в данной точке? Что такое оператор? Каков смысл оператора "градиент"? Как обозначается этот оператор? Как вычислить значение градиента функции трех переменных (координат) в данной точке пространства? Что называется дифференциальным уравнением?
3.1.2.
Объясните понятия и термины: внутренние
и внешние силы, замкнутая и открытая
система, импульс Рх
и момент импульса Lx
системы, скорость механической системы
как целого, полная энергия системы Wх ,
упругий и неупругий удар, центр инерции
системы, работа А
,
потенциальная Wп
и кинетическая Wк
энергии , консервативные и диссипативные
силы, потенциальные и не потенциальные
поля, время релаксации t.
Укажите размерности и единицы измерения
названных
физических величин.
,
упругий и неупругий удар, центр инерции
системы, работа А
,
потенциальная Wп
и кинетическая Wк
энергии , консервативные и диссипативные
силы, потенциальные и не потенциальные
поля, время релаксации t.
Укажите размерности и единицы измерения
названных
физических величин.
3.1.3. Как формулируются и следствием каких свойств пространства-времени? В чем преимущество использования законов сохранения по сравнению с детальным решением уравнения движения?
3.1.4. Дайте пояснения к следующим формулам:
 (3.1)
(3.1)
 (3.2)
(3.2)
 (3.3)
(3.3)
 (3.4)
(3.4)

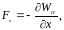 (3.5)
(3.5)
 (3.6)
(3.6)
 (3.7)
(3.7)
3.2. Теоретическое задание
3.2.1. Пользуясь законами Ньютона, докажите, что импульс и момент импульса замкнутой системы есть величины постоянные. Справедливо ли это утверждение, если рассматривается неупругий удар?
3.2.2. Выведите формулу Циолковского
 (3.8)
(3.8)
которая выражает скорость ракеты v , приобретенную за счет выбрасывания продуктов сгорания топлива со скоростью u через начальную массу ракеты m0 и массу m , которую она имеет в момент вычисления скорости.
3.2.3. Докажите, что всегда можно подобрать такую инерциальную систему отсчета, в которой импульс замкнутой системы будет равен нулю. Покажите, что в этой системе центр масс неподвижен.
3.2.4. Докажите законы Кепплера на основании закона сохранения момента импульса замкнутой системы.
3.2.5.
Докажите теорему: кинетическую энергию
системы тел можно представить в виде
суммы двух членов: кинетической энергии
материальной точки массой m
, равной сумме всех масс mi
тел
системы и движущейся как центр масс
системы, и кинетической энергии всех
тел в системе отсчета
жестко
связанной с
центром
масс [см.
формулу (3.7), где
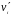 -
скорость тел относительно центра масс
системы].
-
скорость тел относительно центра масс
системы].
3.2.6. Частица находится в стационарном потенциальном силовом поле. Как связана сила, действующая на частицу в каждой точке этого поля с потенциальной энергией частицы?
3.2.7.
Пусть тело движется в вязкой среде под
действием силы тяжести
 ,
причем сила трения пропорциональна
скорости движения
,
причем сила трения пропорциональна
скорости движения
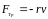 .
Покажите, что время релаксации t
равно отношению массы тела к коэффициенту
сопротивления среды r
, а равновесное значение скорости
.
Покажите, что время релаксации t
равно отношению массы тела к коэффициенту
сопротивления среды r
, а равновесное значение скорости
 .
.
