11. Конвективный теплообмен.

КТО – совместный процесс передачи тепла за счет движения среды (конвекции) и теплопроводности среды. Величина теплового потока состоит из тепловых потоков за счет теплопроводности и за счет конвекции.

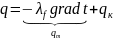
Задачи КТО: смешение теплоносителей разной температуры, задачи теплопередачи и теплоотдачи (теплообмен между поверхностью и подвижной средой).

Закон Ньютона-Рихмана:

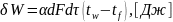
температурный напор.

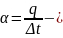коэффициент теплоотдачи, характеризует интенсивность теплообмена между стенкой и средой, числено равен плотности теплового потока при единичном температурном напоре. Находится экспериментально или расчетом.

Задачи КТО сводятся к определению теплового потока через коэффициент теплоотдачи, или через дифференциальное уравнение КТО.

12. Конвективный тепловой поток.

Задачи КТО сводятся к определению теплового потока через коэффициент теплоотдачи, или через дифференциальное уравнение КТО.

Для определения КТП рассматривается канал с площадью сечения 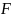, в котором движется теплоноситель с параметрами со скоростью . ТН проходит по каналу расстояние 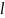за время 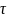, занимая объем . Количество тепла, внесенное ТН в объем:

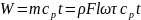
Плотность теплового потока (конвективная составляющая):

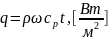
Полный тепловой поток:

Полный тепловой поток можно разделить на составляющие по координатам, в которые входят составляющие скорости 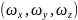и градиента температур 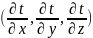. Эти составляющие находят из решения дифференциальных уравнений движения и переноса тепловой энергии.

13. Тепловой и гидродинамический пограничные слои. Режимы течения теплоносителей.

При движении жидкости вдоль стенки всегда образуется динамический пограничный слой, в пределах которого происходит наиболее интенсивное изменение скорости. В зависимости от скорости течения различают ламинарный, переходный и турбулентный пограничные слои.

В зависимости от режима течения изменяются и условия теплоотдачи с поверхности, если стенка и жидкость имеют разную температуру. В этом случае образуется тепловой пограничный слой, в пределах которого наиболее существенно меняется температура. Тепловой пограничный слой обладает термическим сопротивлением .

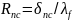Наибольшее значение 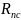имеет ламинарный пограничный слой. Сопротивление турбулентного ПС значительно меньше за счет интенсивного перемешивания и переноса теплоты. Основную часть сопротивления в ТПС имеет образующийся под ним тонкий ламинарный подслой.

14. Дифференциальное уравнение теплоотдачи в ПС.

Уравнения теплоотдачи для ЛПС:

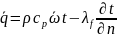
Дифференциальное уравнение теплоотдачи в пограничном слое:

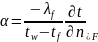
15. Основы теории подобия.

Исследование теплообмена проводится экспериментальным и расчетным путем. Недостаток экспериментального способа в том, что он рассматривает единичные явления. Недостаток расчетного способа – он рассматривает целый класс явлений. Чтобы перейти к единичным явлениям, нужно сформулировать условия однозначности для эксперимента, т.е. задать геометрию области, ТФХ, краевые условия.

Теория подобия рассматривает группы явлений. При анализе и обработке результатов единичных измерений можно получить единое решение для группы явлений. Все явления, входящие в группу, должны удовлетворять условиям геометрического, физического и временного подобия.

Геометрическое подобие. Даны два прямоугольника со сторонами и . Они будут геометрически подобны, если отношение их соответствующих сторон будет одинаково. Величина этого соотношения называется геометрической константой подобия 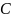. Точки, лежащие в пределах этих прямоугольников и отношение соответствующих координат которых равно , называются сходственными точками.

Физическое подобие. Во всех сходных точках двух систем отношение одноименных функций есть константы.

Временное подобие. Моменты времени, когда в подобных системах происходит одно и тоже событие, называются сходственными моментами времени. Для них всегда можно выбрать одно и тоже значение безразмерного времени.

По методу теории подобия результаты единичных явлений обрабатываются в безразмерном виде и представляются в виде зависимости 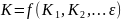. 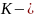безразмерные комплексы, состоящие из размерных физических величин, полученные из соответствующих математических моделей явления. Эти комплексы называются критериями или числами подобия. определяемое число подобия; определяющие числа; 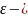поправки. Вид функции определяется статистической обработкой результатов.

Полученное уравнение называется критериальным уравнением или уравнением подобия – приближение аналитически точного решения.

Теоремы теории подобия:

подобные явления характеризуются одинаковым набором чисел подобия;

подобные явления описываются одними и теми же уравнениями подобия;

числа подобия, содержащие элементы условия однозначности, должны быть численно равны.