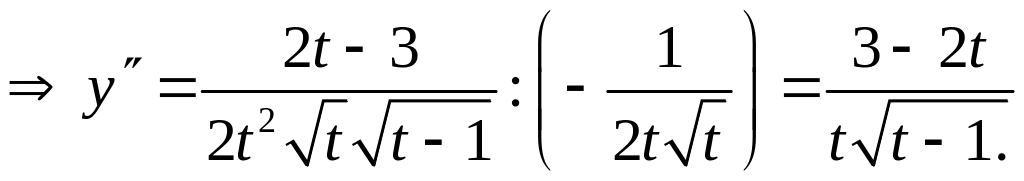4. Правила дифференцирования.
1. Дифференцирование суммы, произведения, частного и обратной функции.
Если функции
![]() и
и
![]() дифференцируемы в точке
дифференцируемы в точке
![]() ,
то в этой точке дифференцируемы функции
,
то в этой точке дифференцируемы функции
![]() (при условии, что
(при условии, что
![]() )
и при этом
)
и при этом
![]() ,
(1)
,
(1)
![]() ,
(2)
,
(2)
 ,
,![]() .
(3)
.
(3)
![]()
Следствие 1:
если функция f
дифференцируема в точке ч и
![]() – постоянная, то, т.е. постоянный множитель
можно выносить из-под знака дифференцирования.
– постоянная, то, т.е. постоянный множитель
можно выносить из-под знака дифференцирования.
Если функция
непрерывна и строго возрастает (убывает)
на отрезке
![]() ,
,
![]() ,
и если существует
,
и если существует
![]() ,
то функция
,
то функция
![]() ,
обратная к функции
,
дифференцируема в точке
,
обратная к функции
,
дифференцируема в точке
![]() ,
причём
,
причём
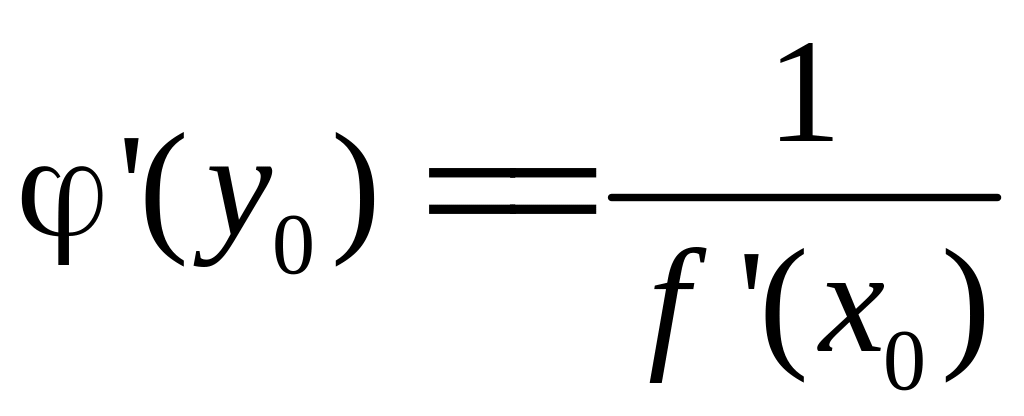 .
(6)
.
(6)
Дифференцирование сложной функции.
Теорема 3:
Если функция
![]() и
и
![]() дифференцируемы соответственно в точках
x0
и y0
, где
дифференцируемы соответственно в точках
x0
и y0
, где
![]() ,
то сложная функция
,
то сложная функция
![]() дифференцируема в точке
дифференцируема в точке![]() ,
причём
,
причём
![]() (8)
(8)
Примеры
Задание 4.
Найти производную
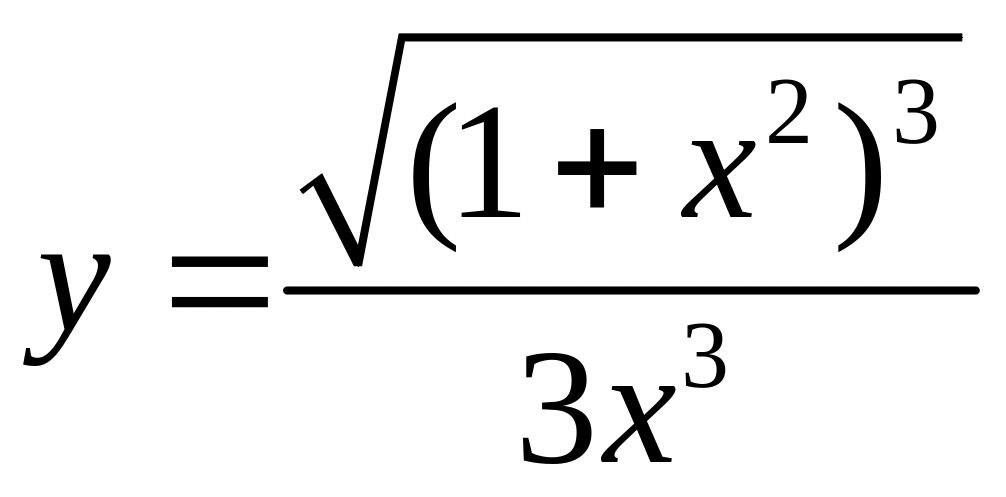 .
.
Решение: Применим формулы дифференцирования частного и сложной функции. Получим:

Задание 4. Найти производную от функции
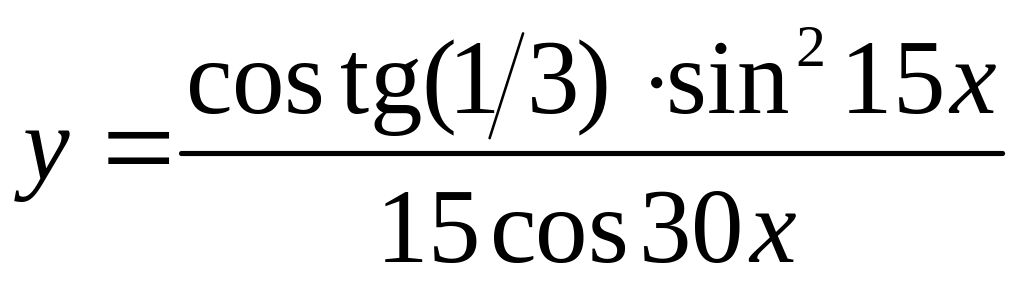 .
.
Решение:
Перепишем функцию в виде:
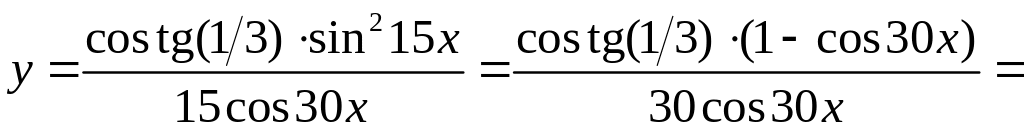
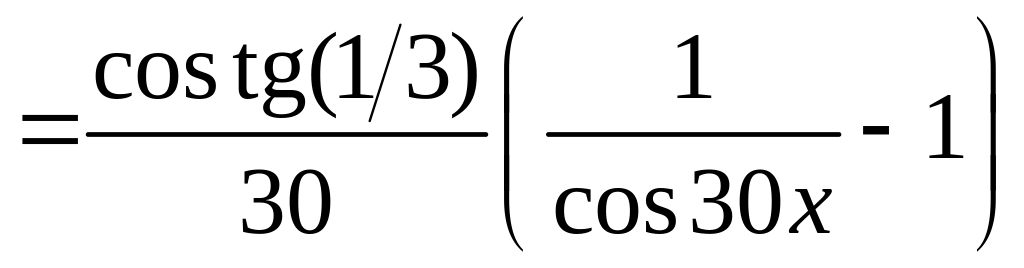 .
.
Применим формулу дифференцирования сложной функции. Получим:
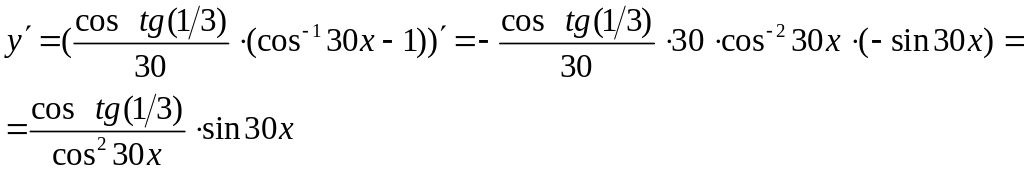
№6 Найти производную от функции
y=![]() .
.
Перепишем функцию в виде:
![]() .
.
Применим формулу дифференцирования сложной функции. Получим:
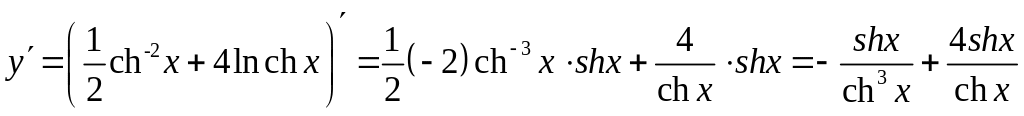
Задание 5. Найти производную от функции
![]() .
.
Решение: Применим формулы дифференцирования суммы и сложной функции. Получим:
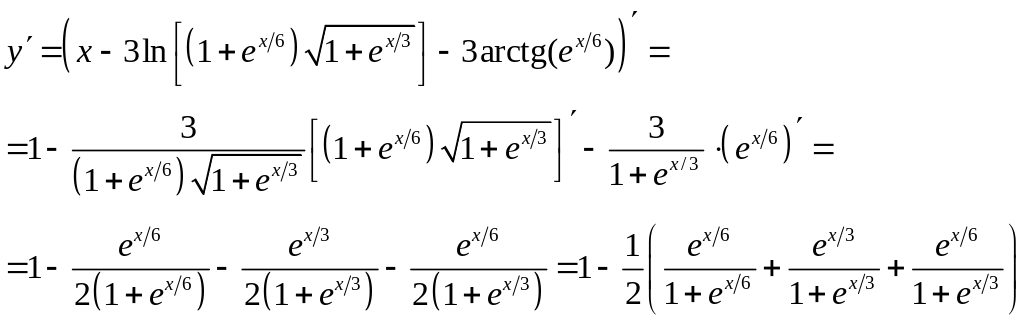
Задание 6. Найти производную от функции
![]()
Решение: Применим формулы дифференцирования сложной функции. Получим:
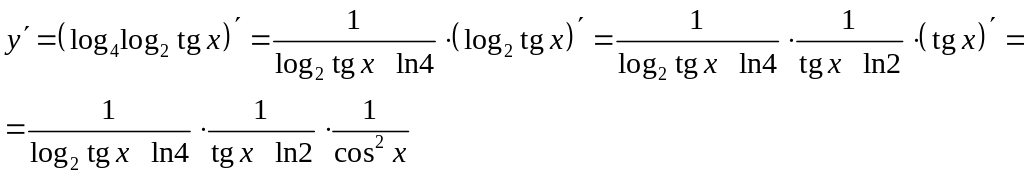
Задание 8. Найти производную от функции
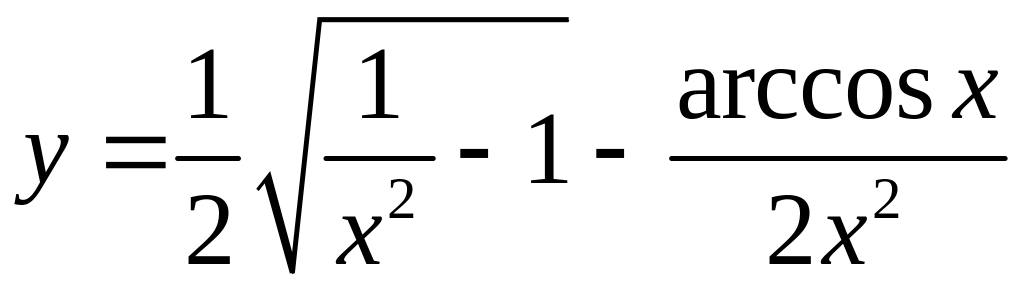
Решение: Применим формулы дифференцирования суммы, частного и сложной функции. Получим:
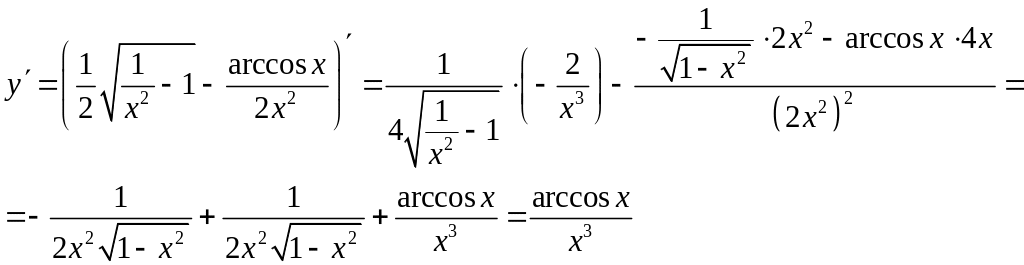
Задание 9. Найти производную от функции
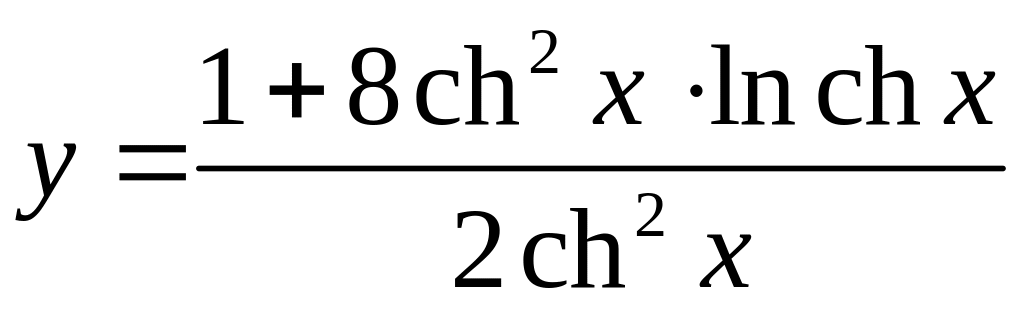 .
.
Решение: Перепишем
функцию в виде:
![]() .
Применим формулы дифференцирования
суммы и сложной функции. Получим:
.
Применим формулы дифференцирования
суммы и сложной функции. Получим:
![]()
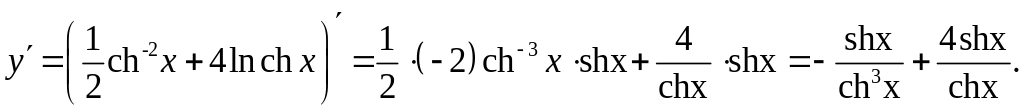
Задание 10. Найти производную от функции
![]() .
.
Решение: Применим логарифмическое дифференцирование. Получим:
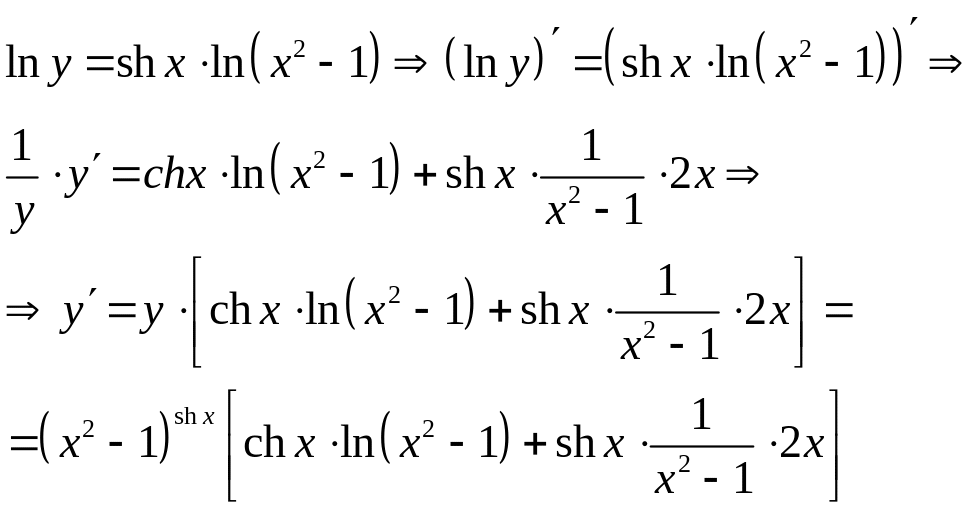
Задание 11. Найти производную от функции.
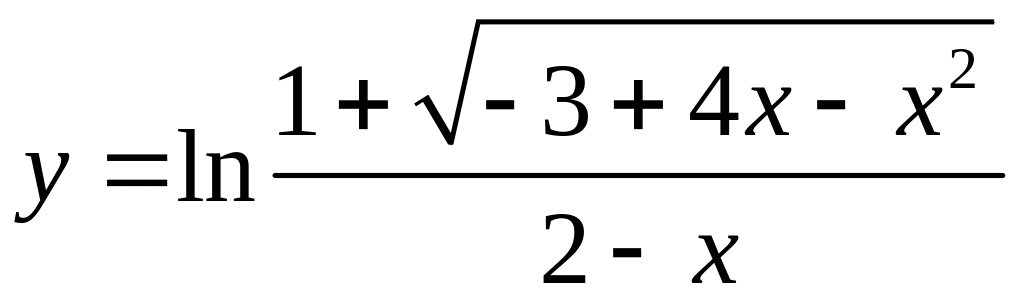 .
.
Решение: Перепишем
функцию в виде:
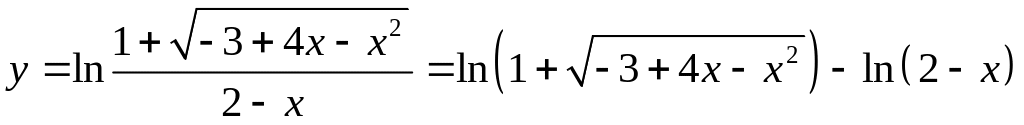
Применим формулы дифференцирования суммы и сложной функции. Получим:

Задание 12. Найти производную от функции
![]() .
.
Решение: Применим формулы дифференцирования суммы и сложной функции. Получим:
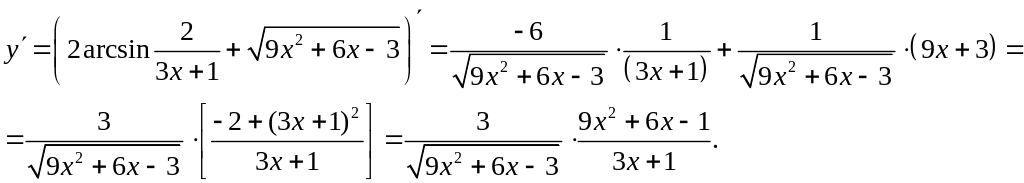
Задание 13. Найти производную от функции
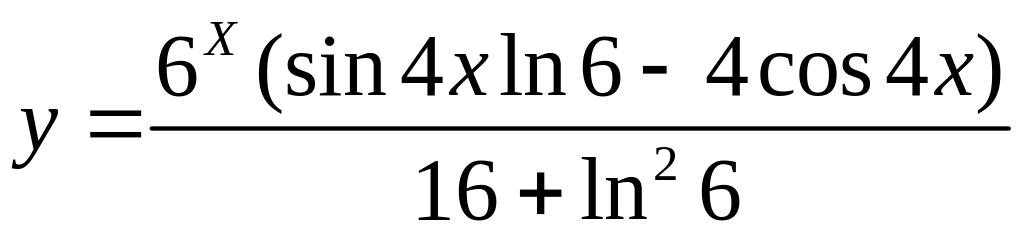
Решение: Применим формулы дифференцирования произведения. Получим:
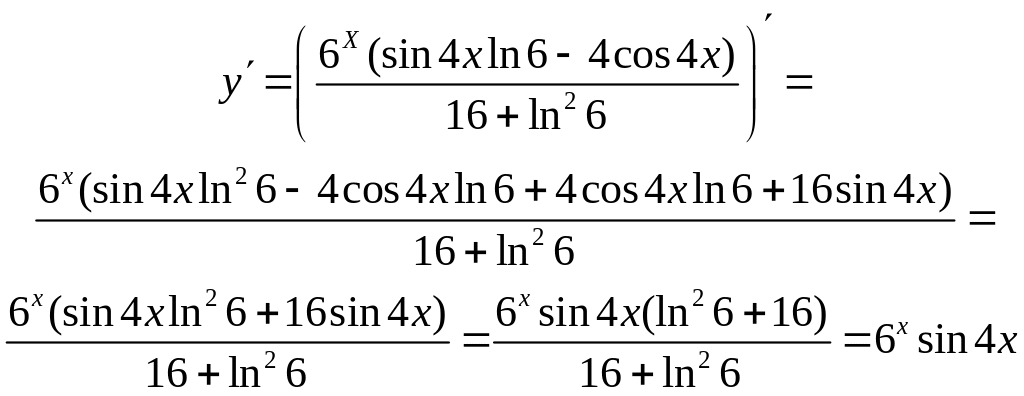
Задание 14.
Найти производную второго порядка
![]() параметрически заданной функции.
параметрически заданной функции.
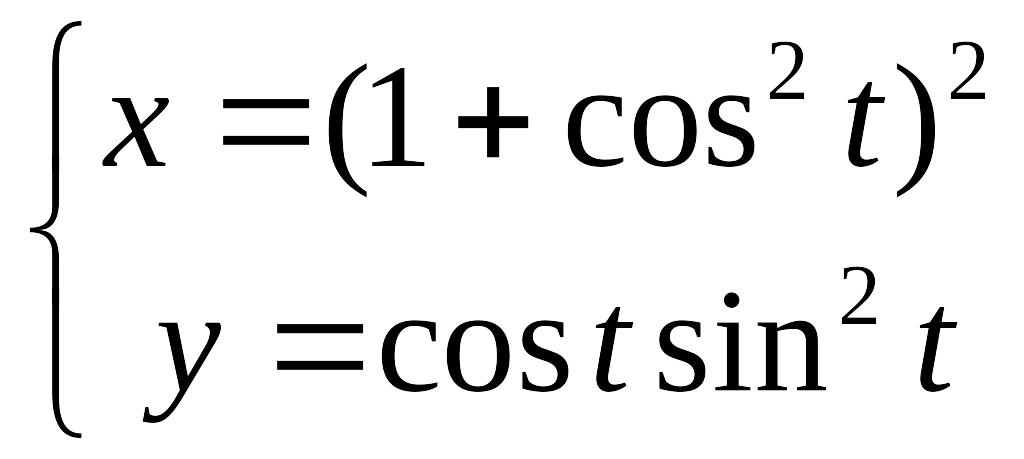
Решение:
Воспользуемся
формулой производной параметрически
заданной функции:
![]()
![]()
У нас
![]()
![]()
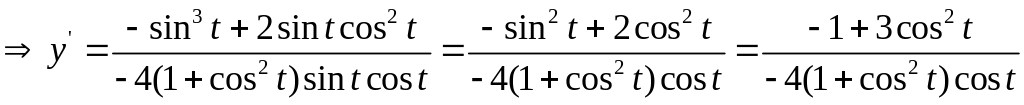
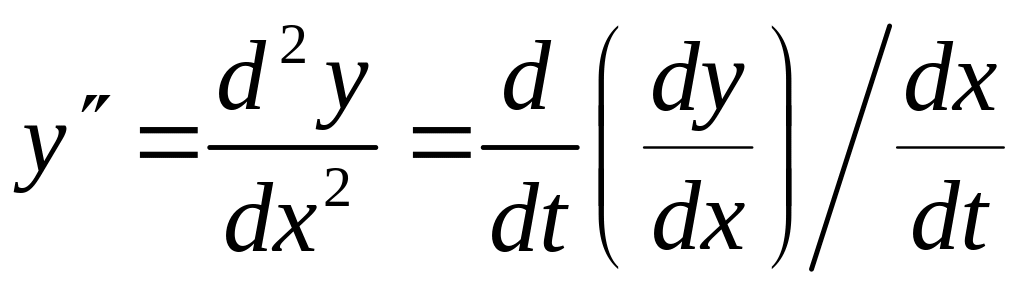
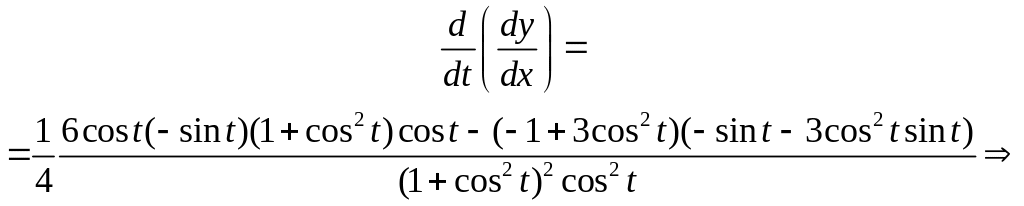
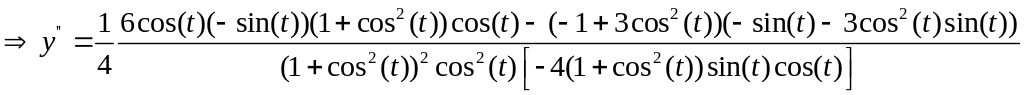
Задание 15.
Составить
уравнение касательной и нормали к кривой
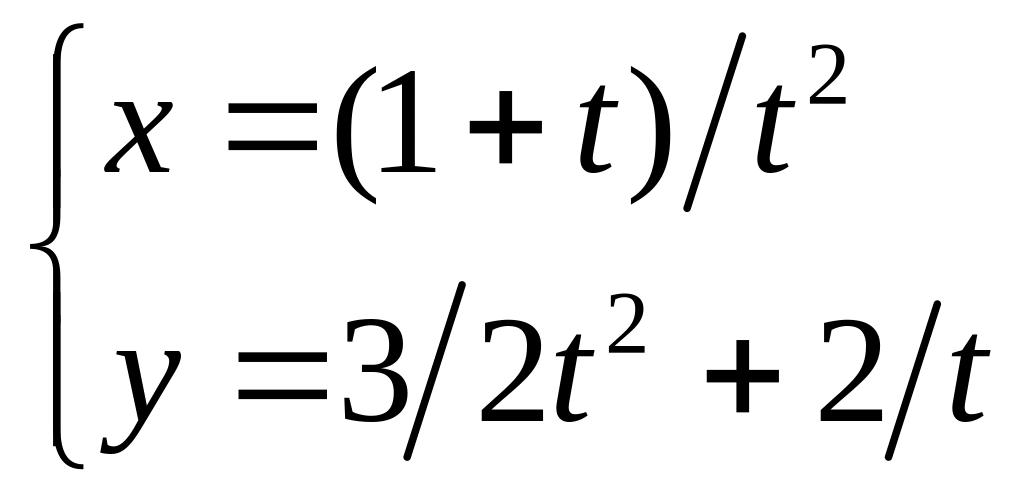 в точке
в точке
![]()
Решение:
Уравнения касательной и нормали к
графику функции, заданной в параметрическом
виде: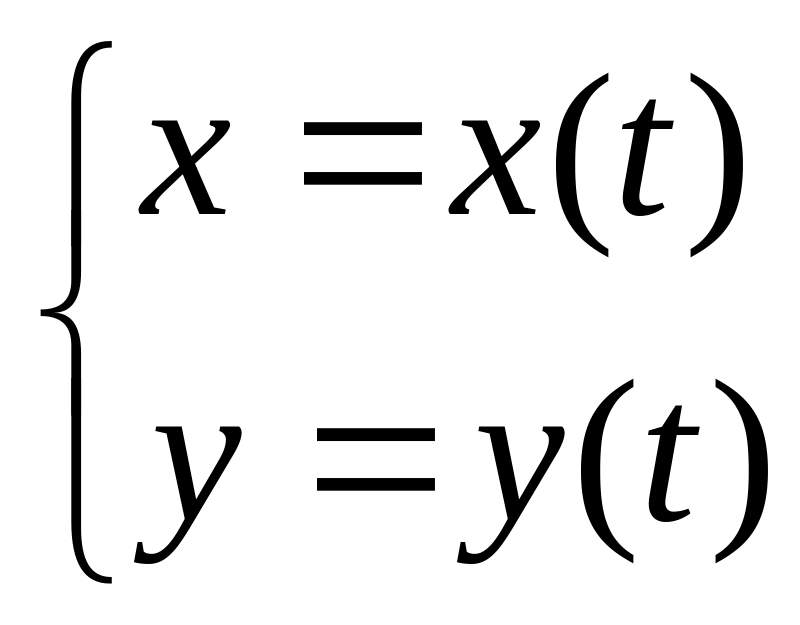 ,
в точке соответствующей значению
параметра
,
в точке соответствующей значению
параметра
![]() ,
имеют вид:
,
имеют вид:
![]() и
и
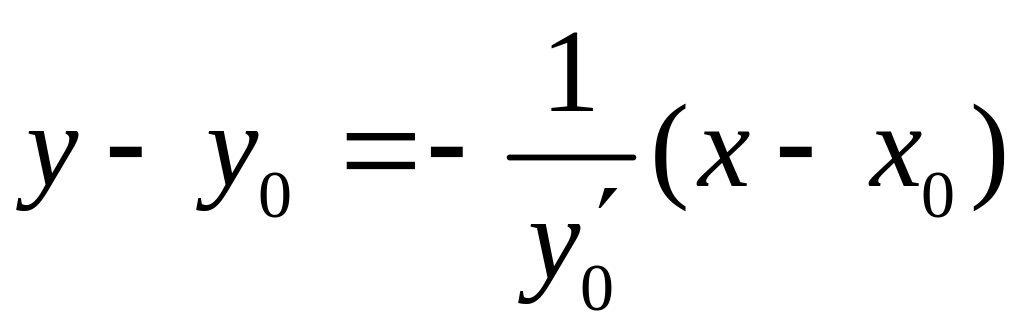 .
Здесь
.
Здесь
![]()
В нашем случае
![]()
Далее,
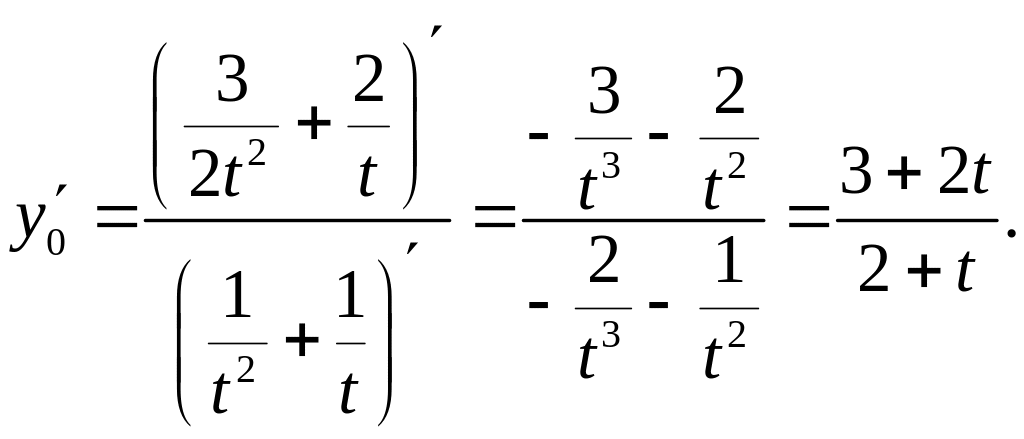 Следовательно,
Следовательно,
![]() Поэтому уравнения касательной и нормали
в точке, соответствующей значению
параметра
Поэтому уравнения касательной и нормали
в точке, соответствующей значению
параметра
![]() имеет
вид:
имеет
вид:
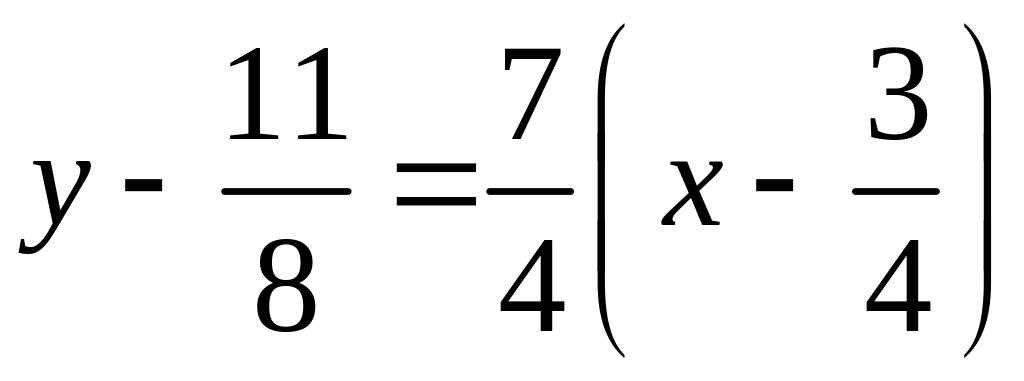 и
и
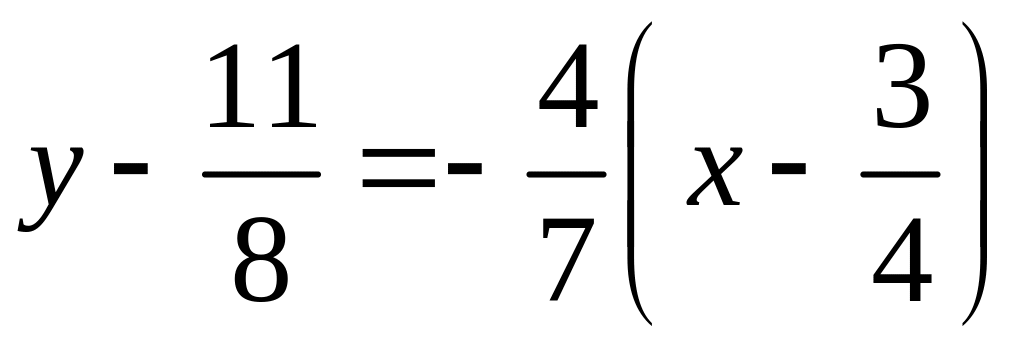 ,
соответственно.
,
соответственно.
Задание 16. Найти
производную n-го
порядка![]() .
.
Решение:
![]() ,
,
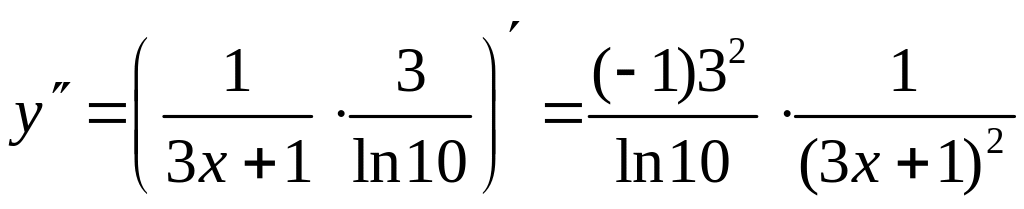 ,
,
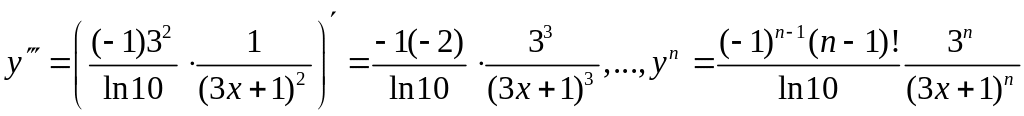 .
.
Задание 17.
Найти производную указанного порядка
![]() .
.
Решение:
![]() .
.
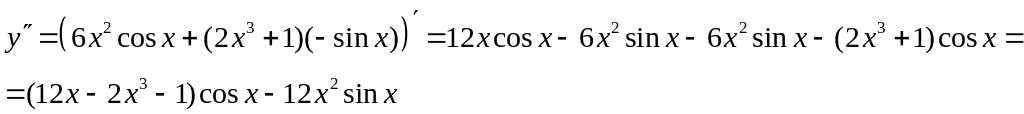
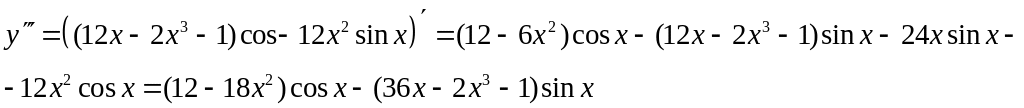
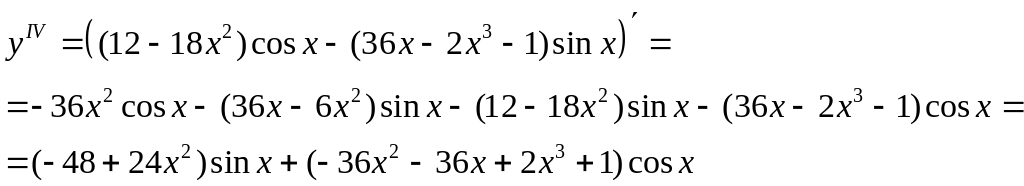
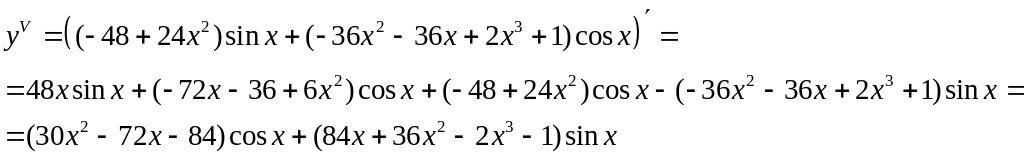
Задание 18. Найти производную второго порядка параметрически заданной функции.
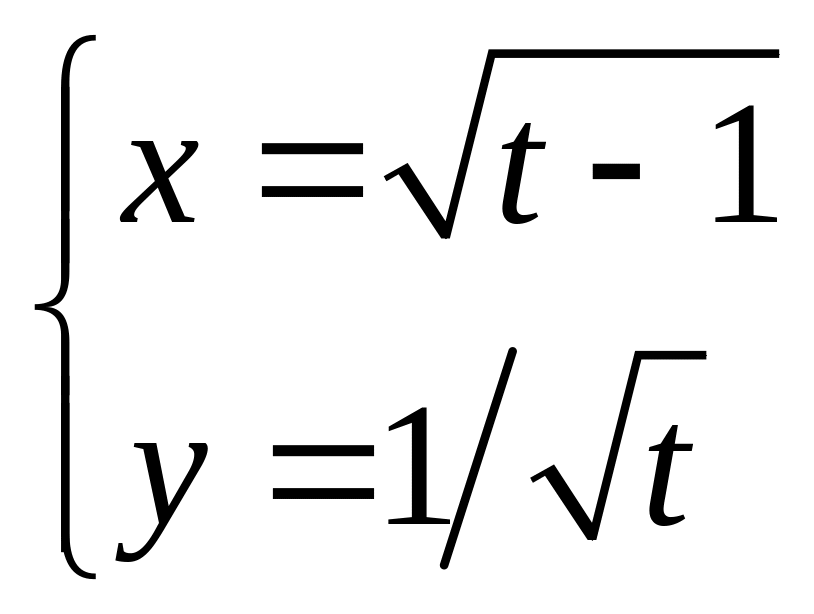
Решение: производная первого порядка параметрически заданной функции вычисляется по формуле:
![]()
У нас:
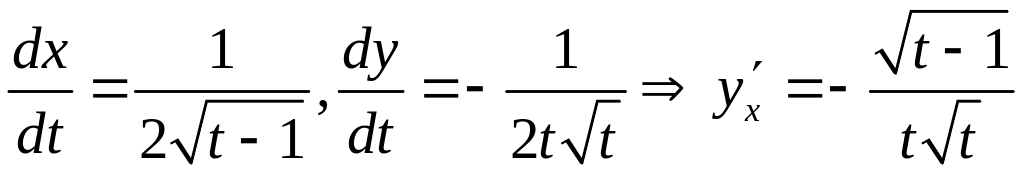
производная второго порядка параметрически заданной функции вычисляется по формуле:
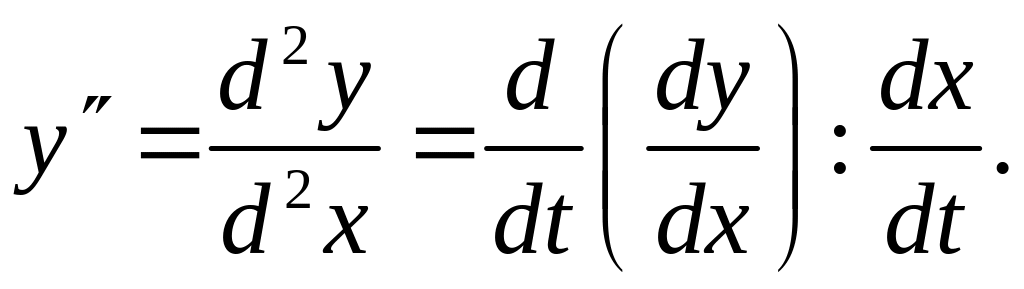
У нас