
СММиФ - 24
.docxКонтрольное задание № 24
1.
Оцените аддитивную, мультипликативную
и тотальную сложность вычисления
значения полинома
 :
:
–при непосредственном вычислении;
– при помощи схемы (алгоритма) Горнера.
Непосредственное вычисление:
P(3) = 2*36 + 3*35 + 5*34 + 5*33 + +4*32 + 4*3 + 1 = 2*729 + 3*243 + 5*81 + + 5*27 + 4*9 + 4*3 + 1 = 1458 + 729 + 405 + 135 + 36 + 12 + 1 = 2776
Схема Горнера:
Задан многочлен p(x):

X = 3
Представим многочлен p(x) следующим образом:





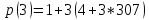


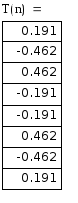
2. Вычислите множество значений дискретного многочлена Чебышева
 для
для

![]()
3.
Вычислить матричное произведение 𝐴𝐵,
если 𝐴
=
 ,
𝐵
=
,
𝐵
=

Вычислите
кронекеровское (прямое) произведение
матриц𝐴 𝐵,
если 𝐴
=
𝐵,
если 𝐴
=
 ,
𝐵
=
,
𝐵
=

Решение:
U=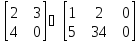 =
= =
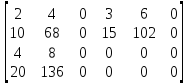
=
=
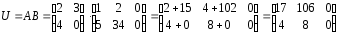
Вычислить значение матрицы 𝑈 = 𝑅 ∨ 𝑆.
U
=
 ∨
∨
 =
=
Решение:

Вычислить значение матрицы 𝐼 = 𝑅 ∧ 𝑆.
𝐼 =
 ∧
∧
 =
=

Вычислить булево произведение матриц
 =
= =
=
Решение:


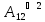




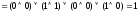




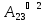







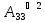
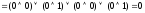
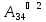










4. Решить в поле Галуа 𝐺𝐹(4) систему уравнений
2𝑥
+

𝑥 + 2𝑦 = 3
Решение:

Первую строку умножим на 2:

Из второй строки отнимем первую:
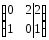
Первую строку умножим на 0,5:

Получаем решение системы в поле Галуа 𝐺𝐹(4):
x=1
y=1
5.
Найти минимальный многочлен
 элемента поля
элемента поля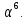 Корни рассматриваем как элементы поля,
построенного с использованием
неприводимого над полем 𝐺𝐹(2)
полинома
Корни рассматриваем как элементы поля,
построенного с использованием
неприводимого над полем 𝐺𝐹(2)
полинома

Решение:
Построим
конечное поле 𝐺𝐹(2),
используя для этого неприводимый
полином Поле состоит из всех многочленов степени
меньше 3:
Поле состоит из всех многочленов степени
меньше 3:
0 xx2
1x+1 x2+1
x2+x
x2+x+1
В качестве α выберем х.все степени по модулю р(х) различны между собой.
x1=x
x2=x2
x3=x+1
x4=x2+1
x5=x2+х
x6= x2+х+1
Ответ:
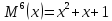
6.а.
Построить порождающую 𝐺
и проверочную
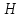 матрицы линейного группового кода с
повторением с параметрами [𝑛;
1; 𝑛],
𝑛
= 6.
матрицы линейного группового кода с
повторением с параметрами [𝑛;
1; 𝑛],
𝑛
= 6.
Решение:
Порождающая матрица состоит из одной строки, так что код с повторением имеет всего два слова: одно содержит только нули, второе – только единицы. Понятно, что кодовое расстояние равно n.
G=(1,1,1,1,1,1)
Проверочная матрица кода имеет (n-1) строк и n столбцов и указывает, что сумма первого и любого другого символов кодового слова должна равняться 0. Число избыточных символов в коде достигает нижней границы, следовательно, коды нечетной длины с повторением относятся к совершенным.
Длина кодового слова n = 6, кол-во информационных символов k = 1, кодовое расстояние dmin= 6, кол-во проверочных символов r = n – k = 5.

6.б.
Определить минимальное расстояние
Хэмминга (кодовое расстояние) кода
спроверочной матрицей
 .
.
dmin = 3.
Стандартное расположение группового кода представляет разложение множества всех возможных n-элементных слов, представляющих собой группу, на смежные классы по подгруппе из 2k кодовых слов
|
000000 |
011000 |
110100 |
101100 |
|
|
|
|
|
|
000001 |
011001 |
110101 |
101101 |
|
000010 |
011010 |
110110 |
101110 |
|
000100 |
011100 |
110000 |
101000 |
|
001000 |
010000 |
111100 |
100100 |
|
010000 |
001000 |
100100 |
111100 |
|
100000 |
111000 |
010100 |
001100 |
|
|
|
|
|
|
000011 |
011011 |
110111 |
101111 |
|
100001 |
111001 |
010101 |
001101 |
|
|
|
|
|
7.а.Используйте
таблицу смежных классов кода (п.6.б) для
контроля над ошибками (обнаружения или
исправления ошибок), если получены
слова:
Процедура исправления ошибок следующая. Принятое кодовое слово анализируют и определяют, в каком столбце оно находится, а затем в качестве исправленного кодового слова берут слово, находящееся в верхней строке.
y1=011001
y2 принят без ошибок
7.б.
Используйте метод синдромного
декодирования линейного группового
кода (п.6.б) для контроля над ошибками,
если получены слова:
Решение:
Получено
слово
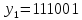 .
. 
Комбинация 011 соответствует первой строке транспонированной проверочной матрицы, что означает, что ошибка произошла в первом информационном разряде.
⇒ ошибок нет
Получено
слово
 .
.
 - ⇒
ошибок нет
- ⇒
ошибок нет
8.а. Источник имеет следующие символы алфавита с их частотами появления:
|
символ |
а |
б |
с |
д |
е |
и |
к |
р |
т |
|
частота |
7 |
12 |
3 |
2 |
9 |
4 |
5 |
8 |
1 |
Постройте кодовое дерево Хаффмана. Постройте кодовое дерево Хаффмана.
Решение:
Алгоритм Хаффмана изящно реализует общую идею статистического кодирования с использованием префиксных множеств и работает следующим образом:
1. Выписываем в ряд все символы алфавита в порядке возрастания или убывания вероятности их появления в тексте.
2. Последовательно объединяем два символа с наименьшими вероятностями появления в новый составной символ, вероятность появления которого полагаем равной сумме вероятностей составляющих его символов. В конце концов построим дерево, каждый узел которого имеет суммарную вероятность всех узлов, находящихся ниже него.
3. Прослеживаем путь к каждому листу дерева, помечая направление к каждому узлу (например, направо - 1, налево - 0) . Полученная последовательность дает кодовое слово, соответствующее каждому символу.
Построим кодовое дерево для сообщения со следующим алфавитом:
|
символ |
а |
б |
с |
д |
е |
и |
к |
р |
т |
|
частота |
7 |
12 |
3 |
2 |
9 |
4 |
5 |
8 |
1 |
|
|
б |
е |
р |
а |
к |
и |
с |
д |
т |
|
|
12 |
9 |
8 |
7 |
5 |
4 |
3 |
2 |
1 |
|
|
б |
е |
р |
а |
к |
и |
с |
дт |
|
|
|
12 |
9 |
8 |
7 |
5 |
4 |
3 |
3 |
|
|
|
б |
е |
р |
ск |
дти |
а |
|
|
|
|
|
12 |
9 |
8 |
8 |
7 |
7 |
|
|
|
|
|
рдти |
ска |
б |
е |
|
|
|
|
|
|
|
15 |
15 |
12 |
9 |
|
|
|
|
|
|
|
рдтиб |
скае |
|
|
|
|
|
|
|
|
|
27 |
24 |
|
|
|
|
|
|
|
|
|
рдтибскае |
|
|
|
|
|
|
|
|

8.б. Запишите код Хаффмана.
|
буква |
код |
|
б |
01 |
|
и |
001 |
|
т |
0001 |
|
д |
0000 |
|
е |
10 |
|
а |
110 |
|
с |
1110 |
|
к |
1111 |
9.
Записать матричное соотношение расчета
апериодической (линейной) дискретной
функции взаимной корреляции
последовательностей
 Вычислить коэффициенты корреляции,
построить график корреляционной функции.
Вычислить коэффициенты корреляции,
построить график корреляционной функции.
Решение:
Апериодическая
взаимокорреляционная функция для
последовательностей
 и
и
 длины N
и M
определяется как
длины N
и M
определяется как
 .
.
Это выражение можно записать в матричной форме.



10
. Записать матричное соотношение расчета
периодической (циклической) дискретной
функции взаимной корреляции
последовательностей
 Вычислить коэффициенты корреляции,
построить график корреляционной функции.
Вычислить коэффициенты корреляции,
построить график корреляционной функции.
Решение аналогично приведенному в задании 9:
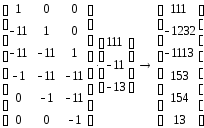

11. Алгоритм «разделяй и властвуй». Вычисление полинома в точках с помощью алгоритма «разделяй и властвуй». Привести пример.
Алгоритм «разделяй и властвуй»
Разделяй и властвуй (англ. divide and conquer) – важная парадигма разработки алгоритмов, заключающаяся в рекурсивном разбиении решаемой задачи на две или более подзадачи того же типа, но меньшего размера, и комбинировании их решений для получения ответа к исходной задаче. Разбиения выполняются до тех пор, пока все подзадачи не окажутся элементарными.
Умножение
двух 2n–значных
чисел легкосводится к четырем умножениям
n-значных
чисел. По методу Карацубы (метод «разделяй
и властвуй») достаточно трех таких
умножений. Запишем 2n-значное
число в виде
![]() .
Легко проверяется тождество:
.
Легко проверяется тождество:
![]() Подобным
образом можно поступить в случае
умножения двух многочленов степени
2n-1
в кольце полиномов над полем Галуа
GF(2).
Подобным
образом можно поступить в случае
умножения двух многочленов степени
2n-1
в кольце полиномов над полем Галуа
GF(2).
Пусть многочлены p(x) и q(x) степени 2n-1 представлены в виде

где
![]() - многочлены степени n-1.
- многочлены степени n-1.
Тогда
произведение многочленов
![]() можно
представить в виде
можно
представить в виде
 (1)
(1)
Введем обозначения
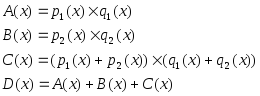
Тогда формула (1) перепишется в виде
![]()
Как видно, использовано только три вместо четырех умножений многочленов степени n. Систематическое применение этого приема соответствует рекурсивной схеме, «разверткой» которой при различных базисах рекурсии можно получить явные схемы умножения, рассматриваемые ниже. Развертка рекурсии производится до того момента, пока не придем к умножению элементарных полиномов.
Список использованной литературы
-
Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженеров. - М.: Энергия, 1988. - 480 с.
-
Лекции по теории графов / Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. – М.: Наука, 1990. – 384 с.
-
Новиков Ф.А. Дискретная математика для программистов. – СПб: Питер, 2000.–304 .
-
Яблонский С.В. Введение в дискретную математику. – М.: Наука, 1986. – 384 с.
-
Андерсон Дж. А. Дискретная математика и комбинаторика.: Пер. с англ. М.: Вильямс, 2004.
-
Теория прикладного кодирования: Учеб.пособие. В 2т./ В.К. Конопелько, А.И. Митюхин и др.; Под ред. проф. В.К. Конопелько. Мн.: БГУИР, 2004.
-
Лидл Р., Нидеррайдер Г. Конечные поля: В 2т. М.: Мир, 1988.
-
4 Хаггарти Р. Дискретная математика для программистов. Москва: Техносфера, 2005.
-
Лосев В.В. Микропроцессорные устройства обработки информации. Алгоритмы цифровой обработки: Учеб.пособие. Мн.: Вышэйшая школа, 1990.
-
Митюхин А.И. Элементы абстрактной алгебры: Учеб.пособие. Мн.: БГУИР, 2001.
-
Овсянников В.А. Методы формирования и цифровой обработки сигналов. Учебное пособие для студентов специальности «Радиосвязь, радиовещание и телевидение» в 2-ух частях. Мн.: БГУИР 2010.
