ТЭС

ВАРИАНТ №227 – Х.

Задача №1.

p=2; m=2; n=7.

1. Формулы для расчета спектральных коэффициентов ряда Фурье в тригонометрической форме:

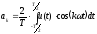
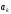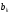, – весовые коэффициенты, 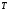– интервал разложения.

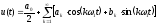– ряд Фурье в тригонометрической форме.

2. Вычисление спектральных коэффициентов для сигнала, приведенного на рис.1.

Интервал разложения равен .

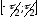Число спектральных коэффициентов n=5.

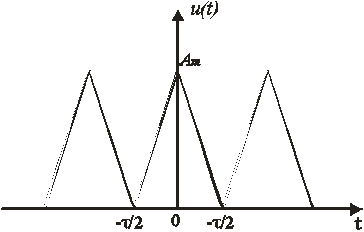
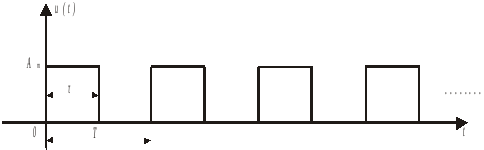
Рис.1.

Исходные данные:

сигнал

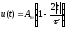
длительность сигнала .

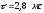амплитуда сигнала .

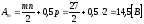Решение:

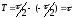– интервал разложения, .

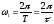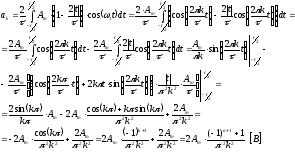
Постоянная составляющая:

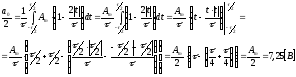
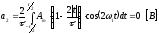
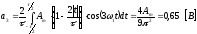
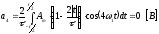
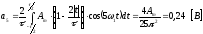
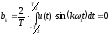, т. к. функция четная.

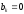
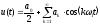
Задача №2.

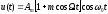1. Для сигнала найти спектральную плотность и амплитудный спектр сигнала.

Исходные данные:

;

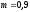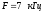
амплитуда сигнала .

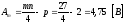2. Построение временной и спектральной диаграммы сигнала.

Решение:

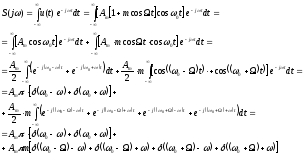
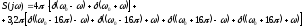
Задача №3.

1. Определение автокорреляционной функции (АКФ) сигнала и формула для её расчета.

Под автокорреляционной функцией сигнала 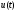понимают величину:

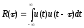
АКФ – операция свертки двух функций 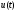и .

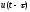2. Для заданного сигнала 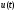определить АКФ графическим способом.

Исходные данные:

;

амплитуда сигнала .

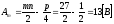Решение:

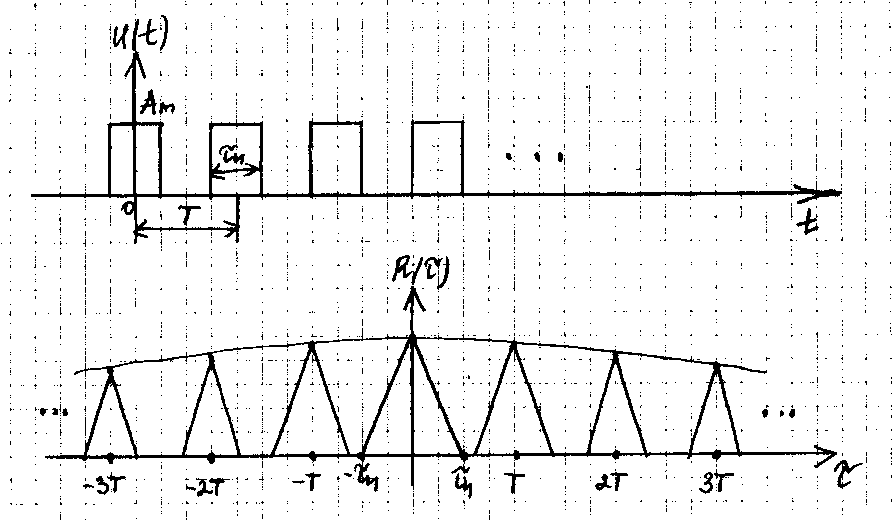
Максимум АКФ достигается при . Если задержка оказывается кратной периоду последовательности (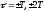), то наблюдаются побочные лепестки АКФ, сравнимые по высоте с главным лепестком.

Задача №4.

1. Формула для определения энергии:

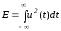
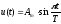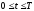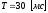2. Определить энергию сигнала ; интервал времени существования сигнала: ; ; амплитуда сигнала .

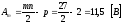Решение:

Задача №5.

Составьте структурную электрическую схему модулятора шумоподобного сигнала (ШПС). Опишите работу модулятора. Электронный ключ модулятора подключен к ячейке регистра, номер которой соответствует номеру группы р=2 потока. В регистре сдвига хранится кодовая комбинация, соответствующая первой букве фамилии студента Х – {00101}

Определить кодовую комбинацию на выходе генератора после поступления 10-p=8-ми тактовых импульсов и период М-последовательности, если длительность каждого импульса шумоподобной последовательности на выходе генератора 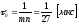. Рассчитать ширину спектра сигнала на выходе генератора ШПС.

Решение:

На рис. 2 приведена схема генератора ШПС, кодированного М-последовательностью. Генератор содержит регистр сдвига с обратными связями и сумматор по модулю два.

Положение управляемого переключателя (7) определяется двоичным числом блока с выхода источника дискретного сообщения. Импульсы с выхода тактового генератора определяют длительность единичного интервала ШПС, а также длительность единичного интервала двоичных кодовых комбинаций на выходе источника дискретных сообщений. В модуляторе производится модуляция косинусоидальной несущей шумоподобными сигналами.

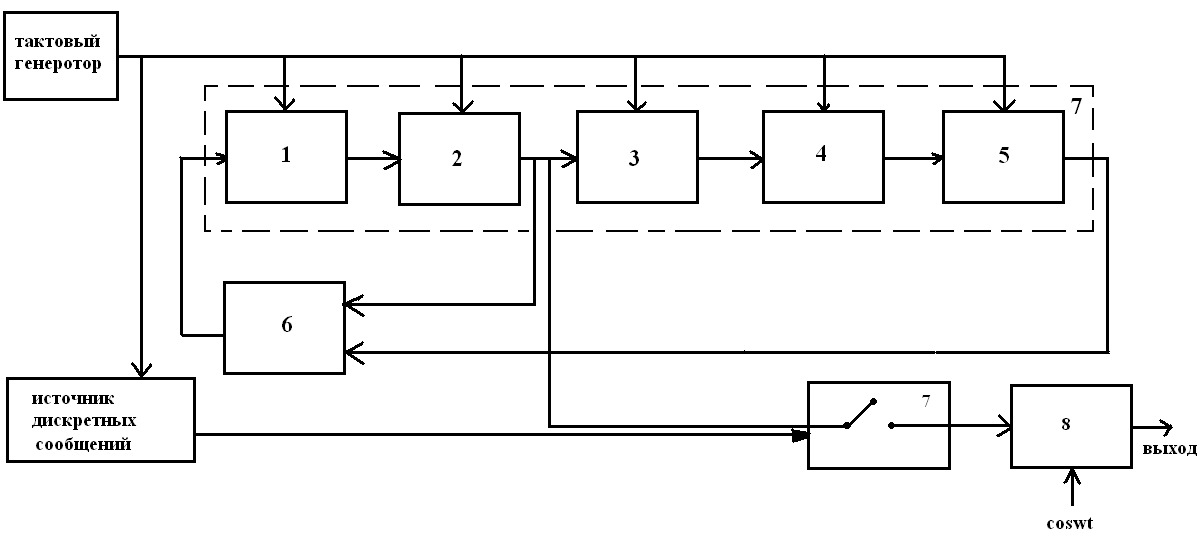
Рис. 2.

1 – 5 – ячейки регистра сдвига

6 – сумматор по модулю 2

7 – управляемый переключатель

8 – фазовый модулятор

Состояния ячеек приведены в таблице.

Номер ТИ	Состояния ячеек регистра сдвига
	1	2	3	4	5
-	0	0	1	0	1
1	1	0	0	1	0
2	1	1	0	0	1
3	0	1	1	0	0
4	1	0	1	1	0
5	0	1	0	1	1
6	0	0	1	0	1
7	1	0	0	1	0
8	0	1	0	0	1

С поступлением последующих ТИ процесс смены состояния ячеек продолжится. В результате на их выходах будет генерироваться ШПС, кодированный циклически сдвинутыми

М-последовательностями.

При непрерывном поступлении тактовых импульсов ШПС периодически повторяется через время, равно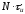е , где 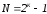– период М-последовательности, определяемый числом разрядов к регистров сдвига (к=5), 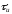– длительность периода тактовых импульсов.

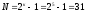
На выходе генератора после поступления 9 ТИ будет следующая кодовая последовательность:

011111010.

Ширина спектра ШПС:

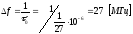
Задача №6

Для заданного конечного числа выборочных значений сигнала и числа выборочных значений импульсной характеристики линейного дискретного фильтра найти:

– коэффициенты дискретного преобразования Фурье;

– коэффициент передачи линейного дискретного фильтра;

– z – преобразование выборочных значений на входе фильтра и на выходе фильтра;

– z – преобразование выборочных значений импульсной характеристики.

Исходные данные:

входной сигнал:

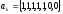
импульсная характеристика:

Решение:

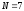
Дискретный сигнал задан семью отсчетами:

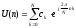
Коэффициенты дискретного преобразования Фурье:

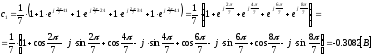
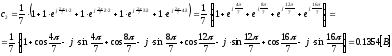
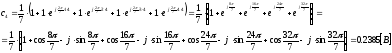
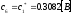
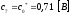
z – преобразование выборочных значений на входе фильтра и на выходе фильтра:

определим выходной сигнал:

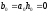
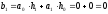
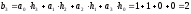
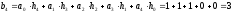
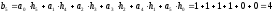
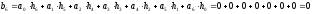
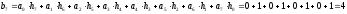
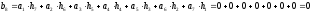
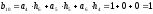
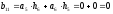
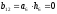
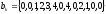
z-преобразование выходного сигнала:

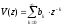
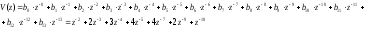
z-преобразование входного сигнала:

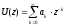
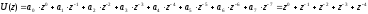
z – преобразование выборочных значений импульсной характеристики:

Системная функция равна отношению z-преобразования выходного сигнала к z-преобразованию входного

,

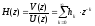где – числовая последовательность, соответствующая импульсной характеристики.

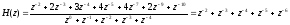
Коэффициент передачи линейного дискретного фильтра:

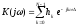
Литература

1. Баскаков С. И. «Радиотехнические цепи и сигналы», М., «Радио и связь», 2000 г.

2. Клюев Л. Л. «Теория электрической связи», Мн., «Дизайн-Про», 1998 г.