
- •1.1 Понятие матрицы. Типы матриц
- •1.2 Алгебра матриц
- •Произведением двух согласованных матриц и
- •2. Определители
- •2.1 Определители квадратной матрицы и их свойства
- •2.2 Теоремы Лапласа и аннулирования
- •3. Обратная матрица
- •3.1 Понятие обратной матрицы. Единственность обратной матрицы
- •3.2 Алгоритм построения обратной матрицы свойства обратной матрицы
Высшая математика
Матрицы и определители
СОДЕРЖАНИЕ
1. Матрицы
1.1 Понятие матрицы. Типы матриц
1.2 Алгебра матриц
2. Определители
2.1 Определители квадратной матрицы и их свойства
2.2 Теоремы Лапласа и аннулирования
3. Обратная матрица
3.1 Понятие обратной матрицы. Единственность обратной матрицы
3.2 Алгоритм построения обратной матрицы Свойства обратной матрицы
Литература
1. Матрицы
1.1 Понятие матрицы. Типы матриц
Прямоугольную таблицу
А=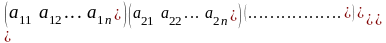 ,
,
состоящую
из m строк и n столбцов, элементами которой
являются действительные числа
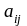 ,
где i
–
номер строки, j
-
номер столбца на пересечении которых
стоит этот элемент, будем называть
числовой матрицей
порядка m´n
и обозначать
,
где i
–
номер строки, j
-
номер столбца на пересечении которых
стоит этот элемент, будем называть
числовой матрицей
порядка m´n
и обозначать
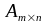 .
.
Рассмотрим основные типы матриц:
1. Пусть m = n, тогда матрица А – квадратная матрица, которая имеет порядок n:
А = .
Элементы
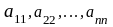 образуют главную диагональ, элементы
образуют главную диагональ, элементы
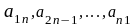 образуют побочную диагональ.
образуют побочную диагональ.
Квадратная матрица называется диагональной, если все ее элементы, кроме, возможно, элементов главной диагонали, равны нулю:
А
=
 = diag (
).
= diag (
).
Диагональная, а значит квадратная, матрица называется единичной, если все элементы главной диагонали равны 1:
Е
=
 = diag (1, 1, 1,…,1).
= diag (1, 1, 1,…,1).
Заметим, что единичная матрица является матричным аналогом единицы во множестве действительных чисел, а также подчеркнем, что единичная матрица определяется только для квадратных матриц.
Приведем примеры единичных матриц:
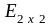 =
=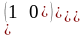 ,
,
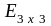 =
= .
.
Квадратные матрицы
А
=
 ,
В =
,
В =

называются верхней и нижней треугольными соответственно.
2. Пусть m = 1, тогда матрица А – матрица-строка, которая имеет вид:
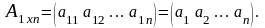
3. Пусть n=1, тогда матрица А – матрица-столбец, которая имеет вид:

4.Нулевой матрицей называется матрица порядка m´n, все элементы которой равны 0:
0
=
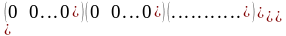
Заметим, что нулевая матрица может быть квадратной, матрицей-строкой или матрицей-столбцом. Нулевая матрица есть матричный аналог нуля во множестве действительных чисел.
5.
Матрица называется транспонированной
к
матрице
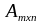 и обозначается
и обозначается
 ,
если ее столбцы являются соответствующими
по номеру строками матрицы
.
,
если ее столбцы являются соответствующими
по номеру строками матрицы
.
Пример.
 Пусть
Пусть
 =
=
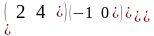 ,
,
тогда
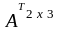 =
=
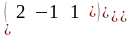 .
.
Заметим, если матрица А имеет порядок m´n, то транспонированная матрица имеет порядок n´m.
6.
Матрица А называется симметричной,
если А=А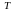 ,
и кососимметричной,
если А = –А
.
,
и кососимметричной,
если А = –А
.
Пример. Исследовать на симметричность матрицы А и В.
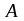 =
=
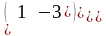 ,
,
тогда
 =
=
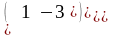 ,
,
следовательно, матрица А – симметричная, так как А = А .
В
=
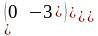 ,
тогда
,
тогда
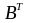 =
=
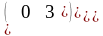 ,
,
следовательно, матрица В – кососимметричная, так как В = – В .
Заметим,
что симметричная и кососимметричная
матрицы всегда квадратные. На главной
диагонали симметричной матрицы могут
стоять любые элементы, а симметрично
относительно главной диагонали должны
стоять одинаковые элементы, то есть
=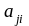 .
На главной диагонали кососимметричной
матрицы всегда стоят нули, а симметрично
относительно главной диагонали
=
–
.
.
На главной диагонали кососимметричной
матрицы всегда стоят нули, а симметрично
относительно главной диагонали
=
–
.
1.2 Алгебра матриц
Рассмотрим действия над матрицами, но вначале введем несколько новых понятий.
Две матрицы А и В называются матрицами одного порядка, если они имеют одинаковое количество строк и одинаковое количество столбцов.
Пример.
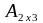 и
и
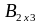 – матрицы одного порядка 2´3;
– матрицы одного порядка 2´3;
и
 – матрицы разных порядков, так как
2´3≠3´2.
– матрицы разных порядков, так как
2´3≠3´2.
Понятия ″больше″ и ″меньше″ для матриц не определяют.
Матрицы
А и В называются равными, если они одного
порядка m´n,
и
=
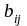 ,
где
,
где
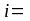 1, 2, 3, …, m, а j = 1, 2, 3, …, n.
1, 2, 3, …, m, а j = 1, 2, 3, …, n.
Умножение матрицы на число.
Умножение матрицы А на число λ приводит к умножению каждого элемента матрицы на число λ:
λА
=
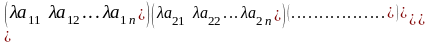 ,
λ
,
λ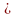 R.
R.
Из данного определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы.
Пример.
Пусть
матрица А =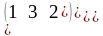 ,
тогда 5А=
,
тогда 5А=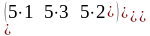 =
= .
.
Пусть
матрица В =
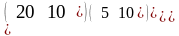 =
=
 = 5
= 5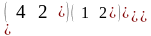 .
.
Свойства умножения матрицы на число:
1) λА = Аλ;
2) (λμ)А = λ(μА) = μ(λА), где λ,μ R;
3) (λА) = λА ;
4) 0ּА = 0.
Сумма (разность) матриц.
Сумма (разность) определяется лишь для матриц одного порядка m´n.
Суммой
(разностью) двух матриц А и В порядка
m´n
называется матрица С того же порядка,
где
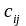 =
±
(
1, 2, 3, …, m,
=
±
(
1, 2, 3, …, m,
j = 1, 2, 3, …, n.).
Иными словами, матрица С состоит из элементов, равных сумме (разности) соответствующих элементов матриц А и В.
Пример. Найти сумму и разность матриц А и В.
=
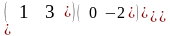 ,
,
 =
=
 ,
,
тогда
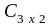 =
+
=
=
+
=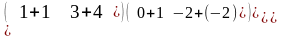 =
=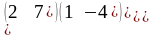 ,
,
 =
–
=
=
–
=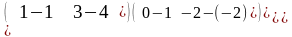 =
=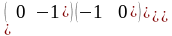 .
.
Если
же
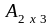 =
=
 ,
,
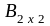 =
=
 ,
,
то А ± В не существует, так как матрицы разного порядка.
Из данных выше определений следуют свойства суммы матриц:
коммутативность А+В=В+А;
ассоциативность (А+В)+С=А+(В+С);
дистрибутивность к умножению на число λ R: λ(А+В) = λА+λВ;
0+А=А, где 0 – нулевая матрица;
А+(–А)=0, где (–А) – матрица, противоположная матрице А;
(А+В) = А + В .
Произведение матриц.
Операция произведения определяется не для всех матриц, а лишь для согласованных.
Матрицы
А и В называются согласованными,
если число столбцов матрицы А равно
числу строк матрицы В. Так, если
,
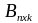 ,
m≠k, то матрицы А и В согласованные, так
как n = n, а в обратном порядке матрицы В
и А несогласованные, так как m ≠ k.
Квадратные матрицы согласованы, когда
у них одинаковый порядок n, причем
согласованы как А и В, так и В и А. Если
,
а
,
m≠k, то матрицы А и В согласованные, так
как n = n, а в обратном порядке матрицы В
и А несогласованные, так как m ≠ k.
Квадратные матрицы согласованы, когда
у них одинаковый порядок n, причем
согласованы как А и В, так и В и А. Если
,
а
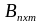 ,
то будут согласованы матрицы А и В, а
также матрицы В и А, так как n = n, m = m.
,
то будут согласованы матрицы А и В, а
также матрицы В и А, так как n = n, m = m.
