Задача по кинематическому и геометрическому расчёту зубчатой передачи

Задача по кинематическому и геометрическому расчёту зубчатой передачи.

Вариант 34.

Задано: Т_вых = 0,3 Н*м; n_вых = 310 мин^-1; i = 3,94.

Определить: d₁, d_a1, d_f1, h, d₂, d_а2, d_f2, a, b₁, b₂, Т_вд, Р_дв, Т_дв, F_t, η.

Рассчитываемый механизм служит для уменьшения скорости вращения электродвигателя в i число раз и состоит из пары находящихся в зацеплении цилиндрических зубчатых колес (шестерни и колеса). Зубчатые колеса устанавливаются на валах, которые поддерживаются в требуемом положении опорами. Каждый вал имеет две опоры (скольжения или качения), закрепленные в корпусе. Быстроходный вал редуктора соединен с валом электродвигателя муфтой. В качестве опор принимаем подшипники качения.

Ориентировочно определяем требуемую мощность Р_дв электродвигателя, приняв предварительно значения КПД:

КПД зубчатой передачи – η_п = 0,9;

КПД подшипника качения – η_п = 0,99;

КПД муфты – η_м = 0,97.

Тогда

Р_дв = k*Р_вых /η [Вт], (1)

где k — коэффициент запаса, учитывающий необходимость преодоления динамических нагрузок в момент разгона, принимаемый равным 1,05 ... 1,1; Р_вых ⁼ Т_{вых *} ω_вых — требуемая мощность на выходном валу; ω_вых = 2πn_вых/60 — угловая скорость выходного вала, рад/с; n_вых — угловая скорость выходного вала в об/; Т_вых — момент на выходном валу, Н*м; η — коэффициент полезного действия электромеханического привода для выбранной схемы он равен

η= 0,97*0,99⁴*0,9 = 0,8386.

Скорость вращения выходного вала в рад/с равна

ω_вых = (2*3,14*310)/60 = 32,45 рад/с.

Подставив значения ω_вых, T_вых, η в выражение (1) и приняв к = 1,1 получим

Р_да = (k* Т_вых*ω_вых)/ η =(1,1*0,3*32,45) = 12,77 (Вт).

Частота вращения электродвигателя

n_дв= n_вых*i = 310*3,94= 1221,4 об/мин.

Из серии двигателей, имеющих скорости вращения 1250, 1280, 1300 обмин выбираем электродвигатель с n = 1250 обмин и мощностью Р> 13 Вт.

Выбираем число зубьев z₁ шестерни. Так как z_min = 17, а рекомендуемое значение числа зубьев шестерни 18 — 30, принимаем z₁= 20. Число зубьев зубчатого колеса определяем по формуле

z₂ = z_1*i = 20*3,94 = 78,8.

Так как колесо должно иметь целое число зубьев, принимаем z₂ = 78. Тогда фактическое передаточное отношение зубчатой передачи

i_ф = z₂/z₁= 78/20 = 4,1.

Относительная погрешность передаточного отношения зубчатой передачи

Допустимая погрешность передаточного отношения не должна превышать 3,5%.

Диаметр ведущего вала, т.е. вала шестерни, принимают близким по размеру диаметру вала двигателя. Считаем, что d_дв > 3 мм.

Выбираем значение модуля m зацепления из стандартного ряда модулей (0,15; 0,2; 0,25; 0,3; 0,4; 0,5; 0,6; 0,8; 1,0; 1,25; ... мм). Применение малых модулей позволяет уменьшить габариты колес или при сохранении габаритов увеличить плавность передачи за счет увеличения числа зубьев. Принимаем m = 0,5, чтобы выполнялось условие, при котором диаметр окружности впадин зубьев d_f-шестерни был бы больше диаметра ее ступицы, т.е. d_f1 > 2d_в.

Предполагая прямозубый тип зубчатых колес, определим диаметр делительной окружности колеса (ведомого звена):

d₂= m*z₂= 0,5 - 78 =39 мм.

Линейная скорость зубчатого колеса в зацеплении

v = ω_вых *d₂/2 = (32,45 - 39 )/(2*10^-3) = 0,633 м/с.

При линейных скоростях v < 6 м/с принимают тип передачи — прямозубая.

У зубчатых колес со стандартной (нормальной) высотой зуба коэффициент высоты головки зуба h_а* = 1, а коэффициент радиального зазора с* зубьев в зацеплении зависит от модуля и равен

с* = 0,5 при m < 0,5 мм;

с* =0,35 при 0,5 < m < 1,0;

с* = 0,25 при m > 1,0 мм.

Высота головки зубьев колес

h_a = h_a* m = 1*0,5 =0,5 мм.

Высота ножки зубьев колес

h_f = m*(h_a* + с*) = 0,5*(1 + 0,5) = 0,75 мм.

Диаметры делительных окружностей зубчатых колес:

шестерни d₁ = m*z₁ = 0,5*20 = 10 мм, колеса d₂ = m*z₂ = 0,5*78 = 39 мм.

Диаметры окружностей вершин зубьев колес:

шестерни d_a1 = d₁ +2*h_a =10 + 2*0,5 = 11 мм, колеса d_a2 = d₂ + 2*h_a= 39 + 2*0,5 = 40 мм.

Диаметры окружностей впадин зубьев колес:

шестерни d_f1 = d₁ – 2*h_f = 10 – 2*0,5 = 8,5 мм, колеса d_f2 = d₂ – 2*h_f = 39 – 2*0,5 = 37,5 мм.

Межосевое расстояние а зубчатой передачи

а = (d₁ + d₂)/2 =(10 + 39 )/2 = 24,5 мм.

Длина b зуба определяется по формуле b = ψ_bd*d, где ψ_bd — коэффициент ширины b венца колеса по диаметру d делительной окружности, рекомендуется принимать ψ_bd = 0,005 ... 0,3.

Длина зуба колеса равна

b₂ = 0,05*39 =1,95 мм.

Принимаем b₂ = 2,2 мм.

Длина зуба шестерни, как более нагруженного звена, определяется по формуле

b₁ = b₂ + (0,5 ... 1,0) мм = 3,5 мм.

Окружное усилие в зацеплении определяется по формуле

F_t = 2Т_вых/d₂ = (2*0,3*10⁵)/39 = 15,385 Н.

Уточняем значение КПД зубчатой пары

где f = 0,1 — коэффициент трения стали по стали (шестерня и зубчатое колесо стальные);

= 1,5 — коэффициент перекрытия пары прямозубых колес; с — коэффициент, учитывающий уменьшение КПД зубчатого зацепления при малых нагрузках Вращающийся момент на ведущем валу зубчатого механизма

Т_вд = Т_вых/( i_ф*η_зз*η_п⁴) = 0,3/(3,94*0,983*0,99⁴) = 0,08064 Н*м.

Вращающий момент на валу электродвигателя

Т_да = Т_дв/ η_м = 0,08064/0,97 = 0,08313 Н*м. Кинематическая схема механизма к задаче приведена на рисунке.

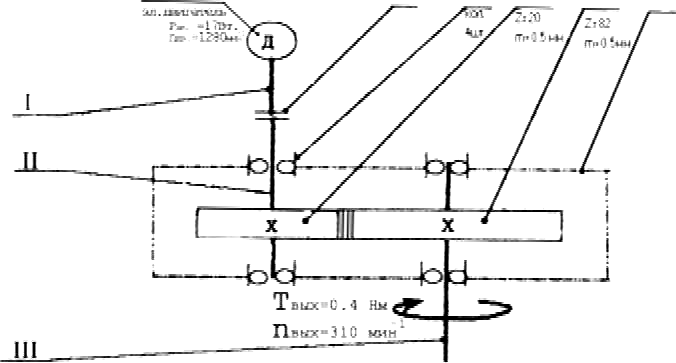
Кинематическая схема механизма: 1 — электродвигатель; 2 — муфта; 3 — опора качения; 4 — шестерня (ведущее зубчатое колесо); 5 - ведомое зубчатое колесо; 6 - корпус; I - вал электродвигателя;

II — ведущий вал; III — выходной вал.