
Примеры с решениями:
Вычислить интегралы:
![]() ;
;

=e-2;

![]() ;
;
 .
.
Преобразуем подынтегральную функцию:
![]()


т.к. во втором интеграле подынтегральная функция нечетная.
Найти площадь фигуры, ограниченной линиями
 и
и 
В
 ыполним
чертеж. Для нахождения площади S
заштрихованной области определяем
пределы интегрирования:
ыполним
чертеж. Для нахождения площади S
заштрихованной области определяем
пределы интегрирования:
![]()
![]()
![]()
![]()
![]()

Примеры для практических занятий.
Вычислить интегралы:
|
|
|
|
|
|
|
|
|
|
|
|
Вычислить площадь фигуры, ограниченной линиями:
|
|
|
|
Ответы:
 ;
;
1;
 ln2;
ln2; ;
; ;
; ;
;2;
2;
a)
 кв.ед.;
кв.ед.;
b)![]() кв.ед. ;
кв.ед. ;
c)
![]() кв.ед.;
кв.ед.;
d)
![]() кв.ед.;
кв.ед.;
Примеры для самостоятельного решения:
Вычислить интегралы:
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;
24)![]() ;
;
 .
.
26) Вычислить площадь фигуры, ограниченной линиями:
 ,
,
 ;
;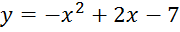 ,
y=0, x=0, x=3;
,
y=0, x=0, x=3; , y=x , x=1, x=1+е ,
y=0;
, y=x , x=1, x=1+е ,
y=0; ,
,
 , x=2, y=0.
, x=2, y=0.
Ответы:
16) ![]() ;
17)
;
17) ![]() ;
18)
;
18) ![]() ;19)
;
20)
;19)
;
20) ![]() ;
21)
;
21) ![]() ;22)
0; 23)
;22)
0; 23) ![]() ;
24) 0; 25) 0;24) a) 4,5 кв.ед.; b)
21 кв.ед;с) 3,5 кв.ед.; d)
;
24) 0; 25) 0;24) a) 4,5 кв.ед.; b)
21 кв.ед;с) 3,5 кв.ед.; d) ![]() +ln2
кв.ед.
+ln2
кв.ед.
Практическое занятие №18.
Несобственные интегралы.
Контрольные вопросы.
1) Выполнение каких условий обязательно при определении интеграла в собственном смысле слова?
2) Можно ли несобственный интеграл рассматривать как предел интегральных сумм с конечным числом слагаемых?
3)Приведите определение несобственного интеграла с бесконечными пределами.
Примеры с решениями:
Вычислить следующие несобственные интегралы с бесконечными пределами или установить их расходимость:
1)
![]() данный
интеграл расходится.
данный
интеграл расходится.
2)![]()
![]()
3)


![]() данный
интеграл сходится.
данный
интеграл сходится.
Примеры для практических занятий:
Вычислить следующие несобственные интегралы с бесконечными пределами или установить их расходимость:
4)![]() 5)
5)
![]() 6)
6)![]() 7)
7)![]() ;
;
8)![]() 9)
9)
![]() ; 10)
; 10)![]() .
.
11)Найти площадь фигуры, ограниченной следующими линиями:
![]()
Ответы:
4) 2; 5)![]() ;
6) расходится; 7)
;
6) расходится; 7) ![]() ;
8) расходится; 9) 1; 10) 1-
;
8) расходится; 9) 1; 10) 1-![]() ;
11)
;
11) ![]() кв.ед.
кв.ед.
Примеры для самостоятельного решения:
12) ![]() 13)
13)![]() ;
14)
;
14)![]()
![]() ;
15)
;
15)![]()
16) ![]() ;
17)
;
17)![]() ;
18)
;
18)![]() ;
19)
;
19)![]()
20)![]() ;
21)
;
21)![]() ;
22) Вычислить площадь бесконечной
полосы, заключенной между кривой
;
22) Вычислить площадь бесконечной
полосы, заключенной между кривой ![]() и осью абсцисс.
и осью абсцисс.
Ответы:
12) 1; 13) 1; 14)
расходится; 15) ![]() ;
16)
;
16)
![]() 17)
17) ![]() ;
18)
;
18) ![]() ;
19) расходится; 20)
;
19) расходится; 20) ![]() ;
;
21) ![]() ;
22)
;
22)
![]() кв.ед.
кв.ед.
Практическое занятие №19.
Положительные ряды.
Контрольные вопросы.
1. Дать определение числового ряда.
2. В каком случае ряд называется сходящимся, в каком – расходящимся?
3. Дать определение суммы, частной суммы и n-го остатка сходящегося ряда.
4. Перечислить свойства рядов.
5. Сформулируйте необходимые признаки сходимости рядов.
6. В чем состоит необходимый и достаточный признак сходимости положительного ряда?
7. Сформулируйте достаточные признаки сходимости положительных рядов:
-признаки сравнения и их предельные формулировка;
-признак Даламбера.




