
Контрольная работа №1 Тема. Численные методы решения задач линейной алгебры, метод Гаусса Задание
Решить систему линейных алгебраических уравнений (СЛАУ)
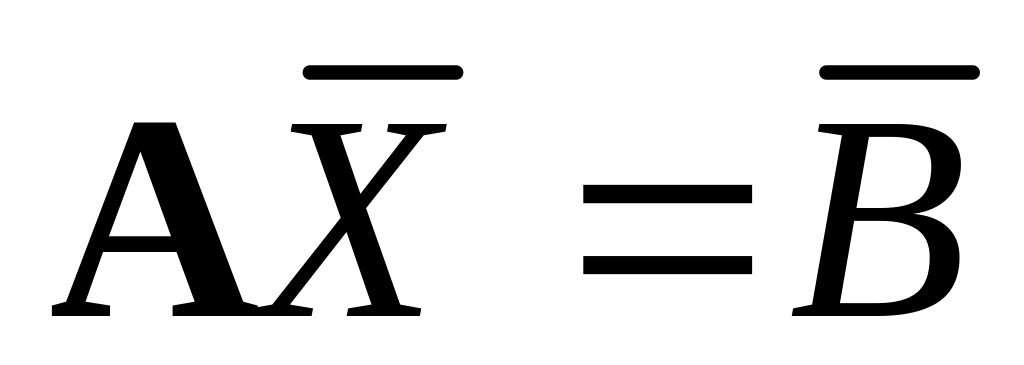 ,
вычислить определитель и обратную
матрицу для матрицы
,
вычислить определитель и обратную
матрицу для матрицы
 методом исключения Гаусса.
методом исключения Гаусса.Сделать выводы о корректности задачи (существование, единственность, устойчивость решения относительно исходных данных).
Решение:
1)
Задана матрица коэффициентов при неизвестных:
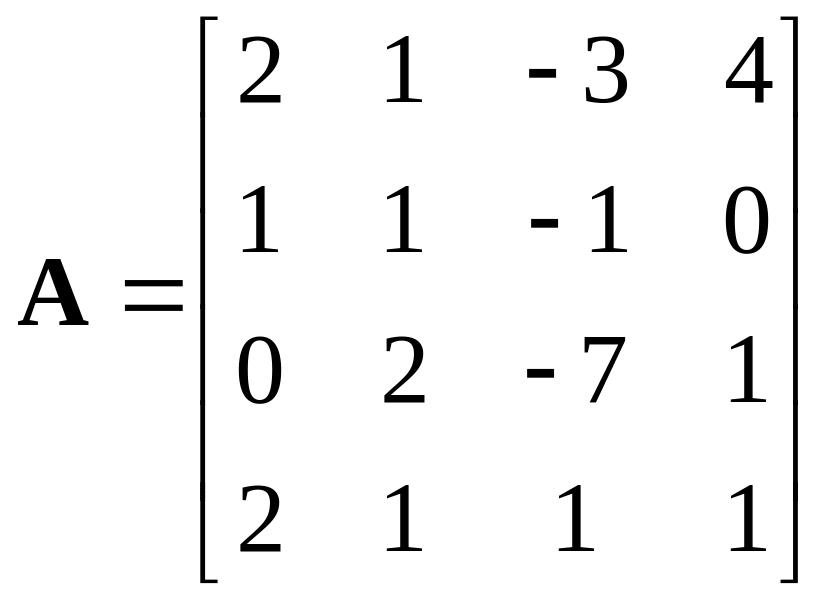 .
.
Вектор правой части зададим самостоятельно:
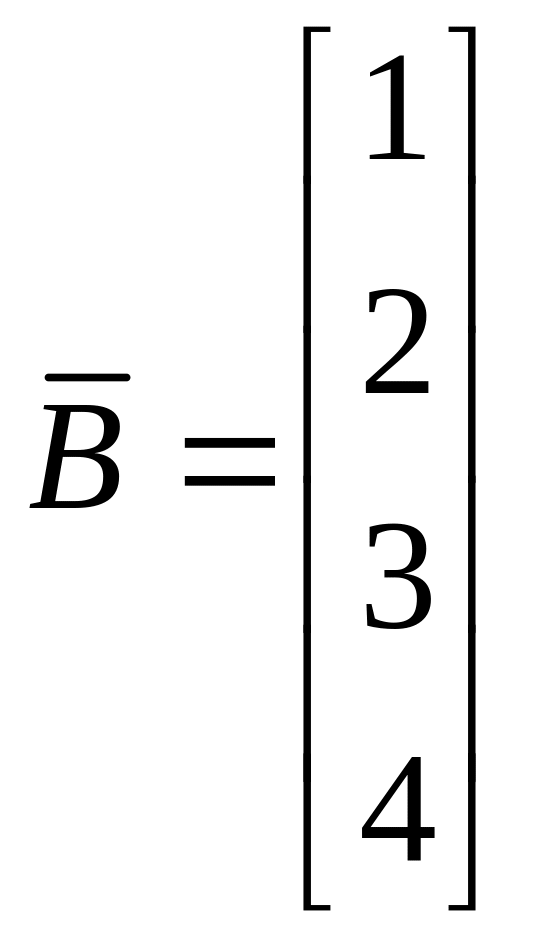 .
.
Для решения заданной системы уравнений воспользуемся методом исключения Гаусса. Решение будем производить в пакете MS Excel.
2)
Откроем чистый лист MS Excel, назовем его «Задание 1». Введем на нем расширенную матрицу системы в ячейки A3:E6.
Производим прямой ход метода Гаусса.
1-ый шаг: делим элементы
первой строки на элемент
![]() .
Для этого в ячейку A8
вводим формулу =A3 / $A$3
и автозаполняем этой формулой ячейки
с A8:E8. Элементы строки A9:E9
получаем по формуле: =A4–A8 (далее
автозаполнние). Элементы строки A10:E10
остаются без изменения, т.е. они равны
соответствующим элементам строки A5:E5.
Элементы строки A11:E11 получаем
по формуле: =A6–A8*$A$6.
Т.о. мы исключили неизвестное
.
Для этого в ячейку A8
вводим формулу =A3 / $A$3
и автозаполняем этой формулой ячейки
с A8:E8. Элементы строки A9:E9
получаем по формуле: =A4–A8 (далее
автозаполнние). Элементы строки A10:E10
остаются без изменения, т.е. они равны
соответствующим элементам строки A5:E5.
Элементы строки A11:E11 получаем
по формуле: =A6–A8*$A$6.
Т.о. мы исключили неизвестное
![]() из 2-го, 3-го и 4-го уравнений.
из 2-го, 3-го и 4-го уравнений.
2-ой шаг: Исключим неизвестное
![]() из всех уравнений, начиная с 3-го. При
этом первое уравнение останется
неизменным, т.е. строка A13:E13
получается по формуле: =A8.
Делим элементы второй строки на элемент
из всех уравнений, начиная с 3-го. При
этом первое уравнение останется
неизменным, т.е. строка A13:E13
получается по формуле: =A8.
Делим элементы второй строки на элемент
![]() расширенной матрицы после первого шага.
Т.о. элементы строки A14:E14
получаем по формуле: =A9 / $B$9.
Элементы строки A15:E15 получаем
так: =A10–A14*$B$10.
Элементы строки A16:E16 неизменны:
=A11.
расширенной матрицы после первого шага.
Т.о. элементы строки A14:E14
получаем по формуле: =A9 / $B$9.
Элементы строки A15:E15 получаем
так: =A10–A14*$B$10.
Элементы строки A16:E16 неизменны:
=A11.
3-й шаг: Исключим неизвестное
![]() из уравнения четыре. При этом первые
два уравнения останутся неизменными,
т.е. строка A18:E18
и строка A19:E19
получены соответственно: =A13
и =A14. Делим элементы
третьей строки на элемент
из уравнения четыре. При этом первые
два уравнения останутся неизменными,
т.е. строка A18:E18
и строка A19:E19
получены соответственно: =A13
и =A14. Делим элементы
третьей строки на элемент
![]() расширенной матрицы после второго шага.
Т.о. элементы строки A20:E20
получаем по формуле: =A15 / $C$15.
Элементы строки A21:E21 получаем
так: =A16–A20*$C$16.
расширенной матрицы после второго шага.
Т.о. элементы строки A20:E20
получаем по формуле: =A15 / $C$15.
Элементы строки A21:E21 получаем
так: =A16–A20*$C$16.
Итак, после 3-го шага матрица коэффициентов
приведена к треугольному виду. При этом
из последнего 4-го уравнения исключены
все переменные, кроме
![]() .
Начиная с этого уравнения, производим
обратный ход метода Гаусса.
.
Начиная с этого уравнения, производим
обратный ход метода Гаусса.
Неизвестная
равна непосредственно элементу вектора
правой части
![]() в полученной после 3-го шага расширенной
матрицы. Т.о. в ячейку H5
записываем значение E21. Значение
неизвестной
запишем в ячейку H4:
=E20-D20*H5. Ячейка H3:
=E19–D19*H5–C19*H4.
И наконец, ячейка H2: =E18–D18*H5–C18*H4–B18*H3.
в полученной после 3-го шага расширенной
матрицы. Т.о. в ячейку H5
записываем значение E21. Значение
неизвестной
запишем в ячейку H4:
=E20-D20*H5. Ячейка H3:
=E19–D19*H5–C19*H4.
И наконец, ячейка H2: =E18–D18*H5–C18*H4–B18*H3.
Итак, решением заданной системы уравнений
является вектор:![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3)
Сделаем проверку полученного решения,
используя надстройку среды MS Excel «Поиск
решения». Для этого зададим расширенную
матрицу в ячейки A26:E29.
В ячейки I26:I29
зададим первое приближение решения
![]() .
В ячейки F29:F29 запишем результат
перемножения матрицы коэффициентов
и вектора неизвестных
.
В ячейки F29:F29 запишем результат
перемножения матрицы коэффициентов
и вектора неизвестных
![]() ,
используя встроенную функцию MS Excel –
МУМНОЖ. Для этого введем в ячейку F26
формулу: =МУМНОЖ(A26:D29;I26:I29).
После чего выделим ячейки F26:F29
нажмем клавишу F2, а затем
сочетание клавиш Ctrl+Shift+Enter.
В ячейки G26:G29
запишем невязку решения
,
используя встроенную функцию MS Excel –
МУМНОЖ. Для этого введем в ячейку F26
формулу: =МУМНОЖ(A26:D29;I26:I29).
После чего выделим ячейки F26:F29
нажмем клавишу F2, а затем
сочетание клавиш Ctrl+Shift+Enter.
В ячейки G26:G29
запишем невязку решения
![]() ,
т.е. в ячейку G26 запишем
формулу: =E26–F26.
После всех приготовления запускаем
надстройку «Поиск решения» (в зависимости
от того какой офис установлен 2003 или
2007/2010 запуск осуществляется немного
по-разному). В появившемся окне «Поиск
решения» в качестве целевой ячейки
ничего не устанавливаем, в качестве
изменяемых ячеек устанавливаем ячейки
I26:I29
и в качестве ограничений записываем,
что G26:G29 = 0. После всех установок
нажимаем кнопку «Выполнить». Как можно
убедится, полученные в ячейках I26:I29
значения мало отличаются от значений
в ячейках H2:H5,
что означает правильность решения.
,
т.е. в ячейку G26 запишем
формулу: =E26–F26.
После всех приготовления запускаем
надстройку «Поиск решения» (в зависимости
от того какой офис установлен 2003 или
2007/2010 запуск осуществляется немного
по-разному). В появившемся окне «Поиск
решения» в качестве целевой ячейки
ничего не устанавливаем, в качестве
изменяемых ячеек устанавливаем ячейки
I26:I29
и в качестве ограничений записываем,
что G26:G29 = 0. После всех установок
нажимаем кнопку «Выполнить». Как можно
убедится, полученные в ячейках I26:I29
значения мало отличаются от значений
в ячейках H2:H5,
что означает правильность решения.
4)
Для оценки существования, единственности
и устойчивости решения найдем определитель
матрицы коэффициентов
и обратную матрицу
![]() .
Для этого используем встроенные в MS
Excel функции МОБР и МОПРЕД. Определитель
матрицы
равен
.
Для этого используем встроенные в MS
Excel функции МОБР и МОПРЕД. Определитель
матрицы
равен
![]() (ячейка J8). Обратная
матрица записана в ячейках J2:M5.
(ячейка J8). Обратная
матрица записана в ячейках J2:M5.
Найдем, для проверки, определитель и обратную матрицу по методу Гаусса вручную.
Запишем матрицу коэффициентов системы и дополним ее справа единичной матрицей:
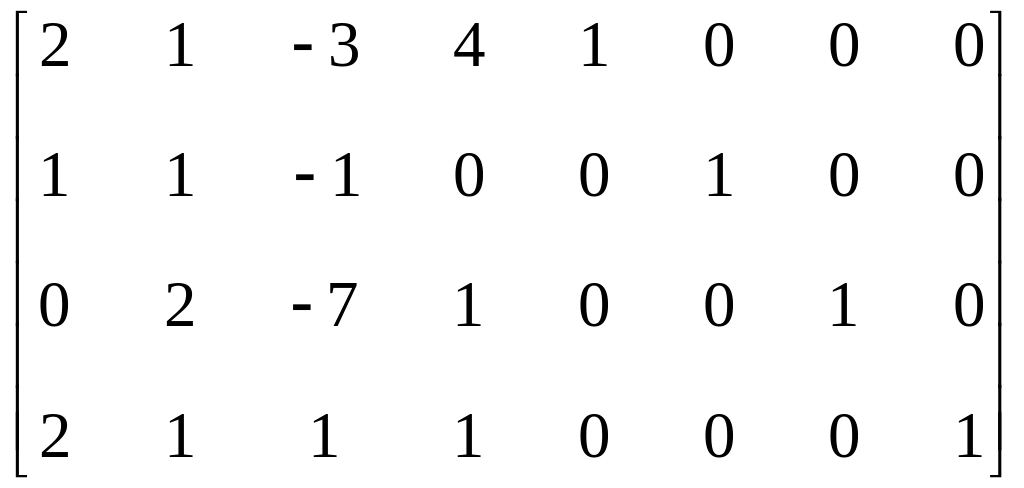 .
.
Производим преобразования по методу Гаусса, т.е. получаем для левой матрицы нижнюю треугольную матрицу.
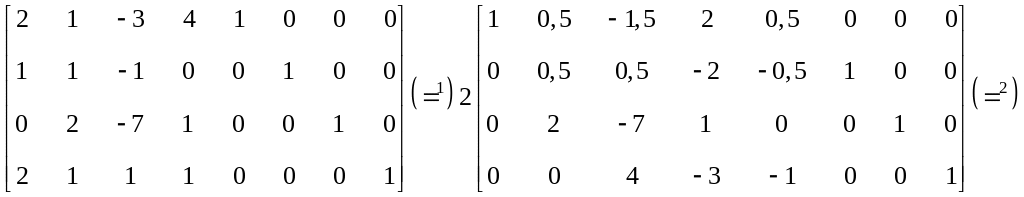
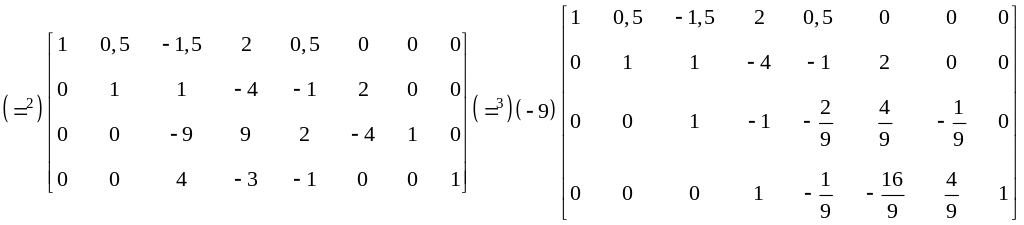
Действие 1: выносим за знак матрицы
коэффициент 2 из строки 1, т.е. делим всю
строку 1 на 2. Полученную строку 1 домножаем
на
![]() и складываем со строкой 2. Строку 1
домножаем на
и складываем со строкой 2. Строку 1
домножаем на
![]() и складываем со строкой 4. Третью строку
не трогаем.
и складываем со строкой 4. Третью строку
не трогаем.
Действие 2: выносим за знак матрицы коэффициент 0,5 из строки 2, т.е. делим всю строку 2 на 0,5. Полученную строку 2 домножаем на и складываем со строкой 3. Четвертую строку не трогаем.
Действие 3: выносим за знак матрицы
коэффициент
![]() из строки 3, т.е. делим всю строку 3 на
.
Полученную строку 3 домножаем на
из строки 3, т.е. делим всю строку 3 на
.
Полученную строку 3 домножаем на
![]() и складываем со строкой 4.
и складываем со строкой 4.
После преобразований мы получили матрицу:
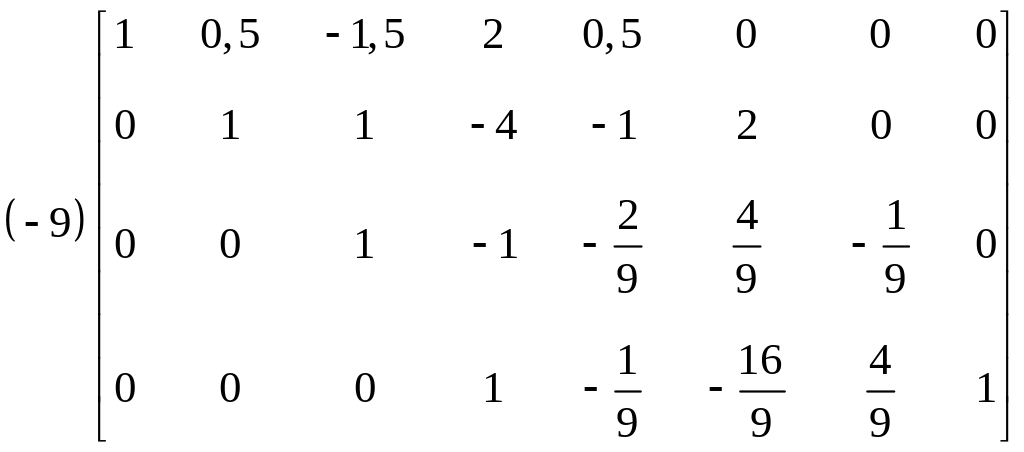 .
.
Коэффициент перед матрицей равен
определителю исходной матрицы
,
т.е.
![]() .
Определитель идентичен найденному в
MS Excel по
формуле МОПРЕД (ячейка
.
Определитель идентичен найденному в
MS Excel по
формуле МОПРЕД (ячейка
![]() ).
).
Для определения обратной матрицы
произведем процедуру метода Гаусса для
полученной матрицы, получая при этом
верхнюю треугольную матрицу, а точнее
проводим преобразования так, чтобы
слева осталась единичная матрица. В
этом случае, матрица, полученная справа
от единичной, будет обратной матрицей
![]() .
.
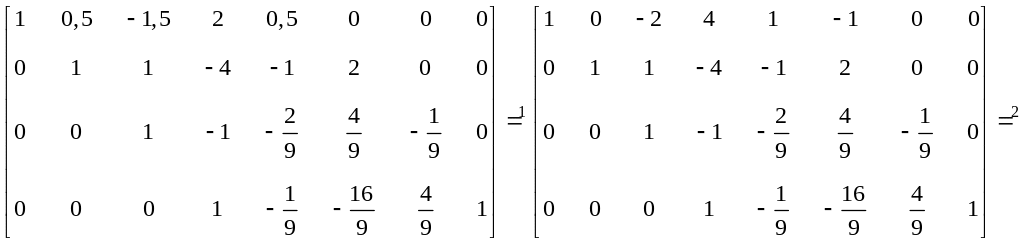
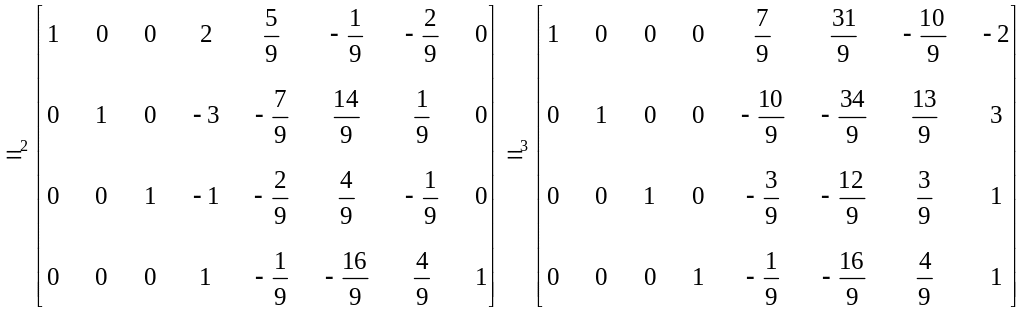
Действие 1: домножаем строку 2 на
![]() и складываем с первой.
и складываем с первой.
Действие 2: домножаем строку 3 на и складываем со строкой 2, затем домножаем строку 3 на 2 и складываем со строкой 1.
Действие 3: строку 4 складываем со строкой 3, затем домножаем строку 4 на 3 и складываем со строкой 2, после чего домножаем строку 4 на и складываем со строкой 1.
В результате получаем обратную матрицу в виде:
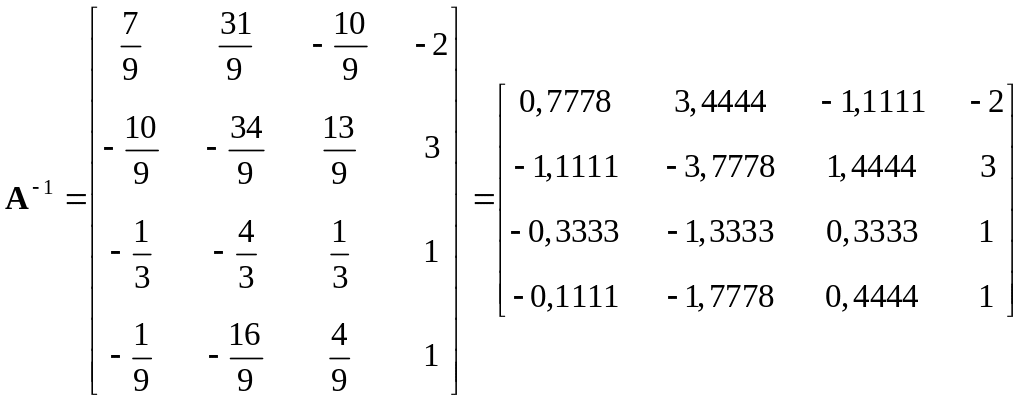 .
.
Итак, полученная матрица полностью совпадает с матрицей, найденной в MS Excel с помощью функции МОБР в ячейках J2:M5.
5)–6)
Как видно, определитель матрицы
коэффициентов не равен нулю, следовательно,
система имеет единственное решение.
Для оценки обусловленности матрицы
найдем меру обусловленности:
![]() .
Здесь
.
Здесь
![]() и
и
![]() – нормы соответствующих матриц. Норму
будем рассматривать в виде:
– нормы соответствующих матриц. Норму
будем рассматривать в виде:
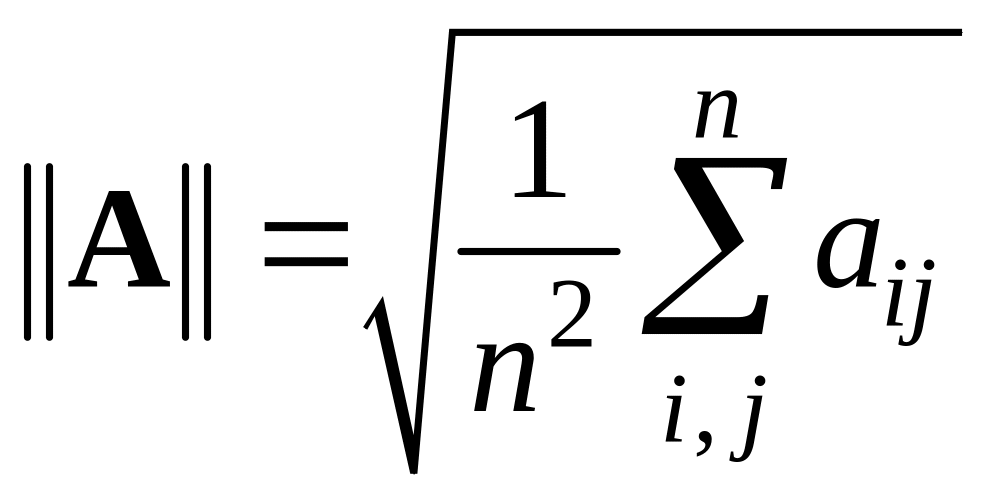 ,
где
,
где
![]() – размер матрицы
(в нашем случае
– размер матрицы
(в нашем случае
![]() ).
Нормы матрицы
и
приведены в ячейках J14
и N14 соответственно,
и они равны
).
Нормы матрицы
и
приведены в ячейках J14
и N14 соответственно,
и они равны
![]() ,
,
![]() .
Мера обусловленности при этом составит:
.
Мера обусловленности при этом составит:
![]() .
Значение меры не очень близко к единице,
однако, обусловленность заданной системы
можно считать хорошей.
.
Значение меры не очень близко к единице,
однако, обусловленность заданной системы
можно считать хорошей.
7)–8)
Для окончательного вывода о корректности
задачи придадим исходной системе малое
возмущение и сравним новое решение со
старым, оценив относительную погрешность
решения в %. Решение будем производить
используя «Поиск решения». Для этого
используем ячейки A33:I36.
В качестве возмущения возьмем изменение
значения элемента
на 0,1, т.е. вместо
![]() рассмотрим систему с
рассмотрим систему с
![]() .
При этом полученное в ячейках I33:I36
решение составляет:
.
При этом полученное в ячейках I33:I36
решение составляет:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Относительная погрешность решения для
каждого значения
.
Относительная погрешность решения для
каждого значения
![]() представлена в ячейках K33:K36.
Средняя относительная погрешность
решения при малом возмущении составляет
5,868%. Отсюда можно сделать вывод, что
малому возмущению соответствует малое
изменение в решении. Т.о. поставленная
перед нами задача является корректной!
представлена в ячейках K33:K36.
Средняя относительная погрешность
решения при малом возмущении составляет
5,868%. Отсюда можно сделать вывод, что
малому возмущению соответствует малое
изменение в решении. Т.о. поставленная
перед нами задача является корректной!
