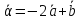Высшая математика кр 1 вар 10
.docx№20
A (-3; -3) B (5; -7) C (7; 7)
-
Уравнение стороны AB найдём по формуле:
AB:
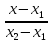 =
=
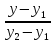 ,
,
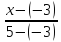 =
=
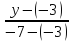 ,
,
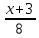 =
=
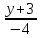 ,
,
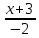 =
=
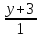
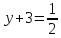
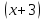 ,
,
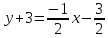 , KAB
= -
, KAB
= -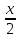
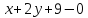
 Уравнение
AB
Уравнение
AB
-
Так как высота CH
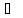 AB,
то KCH
* KAB
=
AB,
то KCH
* KAB
=
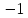 ,
KCH
=
,
KCH
=
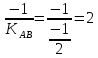
Воспользуемся
формулой
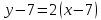 ,
,
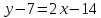 ,
,
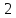
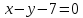
 уравнение
высоты CH
уравнение
высоты CH
Найдём длину высоты CH:
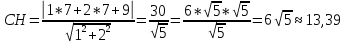 ед.
длина
ед.
длина
-
Медиана АМ делит ВС пополам, т.е. m – середина стороны ВС
Найдём её координаты:
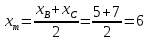
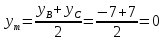 M
(6; 0)
M
(6; 0)
AM:
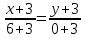 ,
,
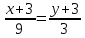
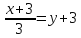 ,
,
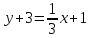
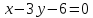 − уравнение
АМ
− уравнение
АМ
-
Чтобы найти координаты N – точки пересечения между АМ и высоты СН, необходимо решить систему, составленную из уравнений этих линий:
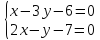
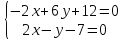
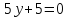
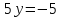

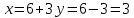
N (3; -1)
-
Так как искомая прямая параллельна стороне АВ и проходит через вершину С, то КАВ = КСD =
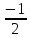
CD:
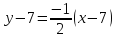
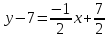
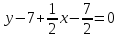
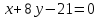 – уравнение
CD
– уравнение
CD AB
AB
-
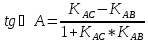 ,
где КАС
найдём из уравнения стороны АС
,
где КАС
найдём из уравнения стороны АС
АС:
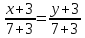
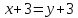 ,
,
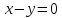 ,
,
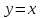
KAC = 1
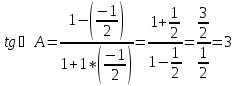
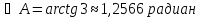
Сделаем рисунок:
№40
A1(2; 3; 5) A2(5; 3; -7) A3(1; 2; 7) A4(4; 2; 0)
-
Уравнение плоскости А1 А2 А3 найдём по формуде:
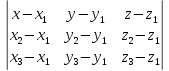 =
0
=
0
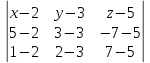 =
0
=
0
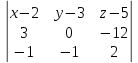 =
0
=
0
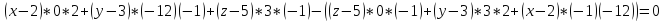
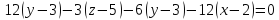
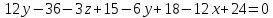
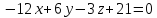
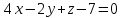 −
A1
A2
A3
−
A1
A2
A3
-
Запишем уравнение прямой, проходящей через точку А4:
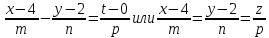
Так
как искомая прямая перпендикулярна А1
А2
А3,
то
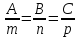
в
нашем случае имеем
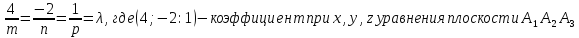

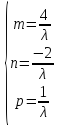
Полученные значения подставим в условие:
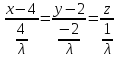 ,
,
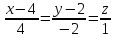
-
Расстояние от А4 ДО А1 А2 А3 найдём по формуле:
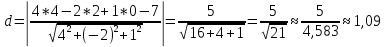
-
Найдём угол между прямой А1 А4 и плоскостью А1 А2 А3:
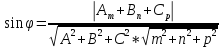
A1A4:
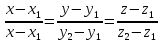
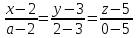
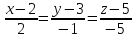 ,
где m
= 2
,
где m
= 2
n = -1
p = -5
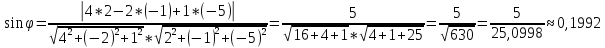
-
Найдём косинус угла между 0xy и А1 А2 А3:
Плоскость
0xy
– z
= 0, т.е.
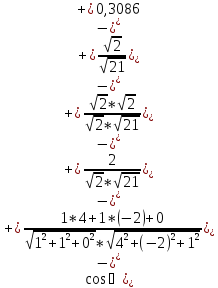
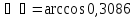
Сделаем чертёж:
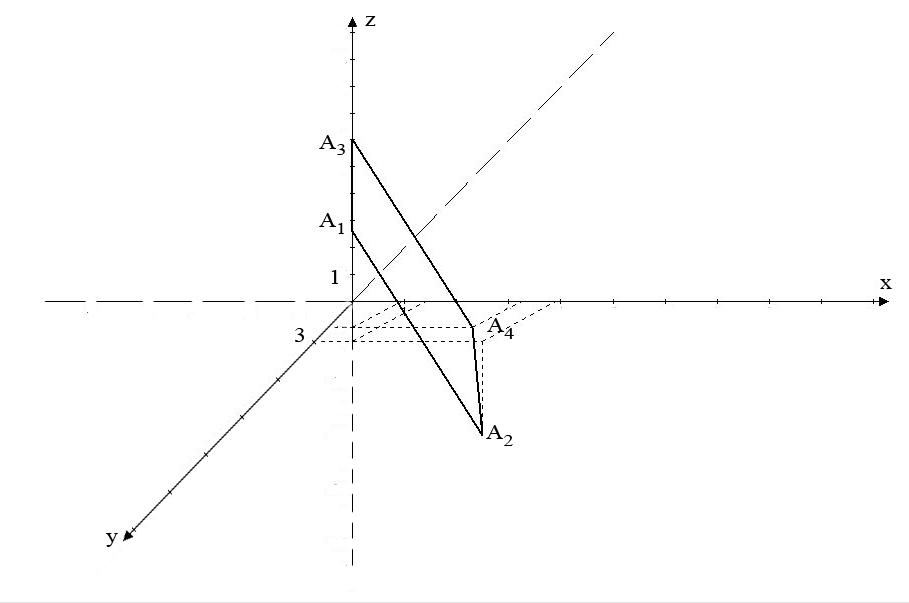
№30
-
b =
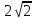 ,
,
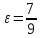
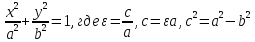
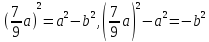
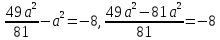
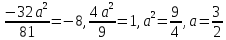
Тогда
уравнение эллипса примет вид: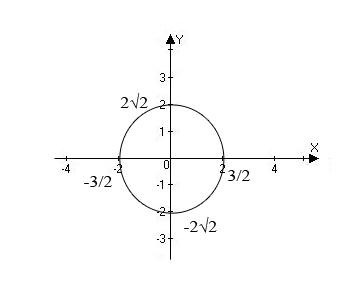
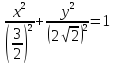
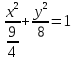
-
Уравнение гиперболы имеет вид:
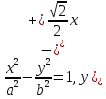
По
условию
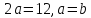

Отсюда
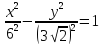
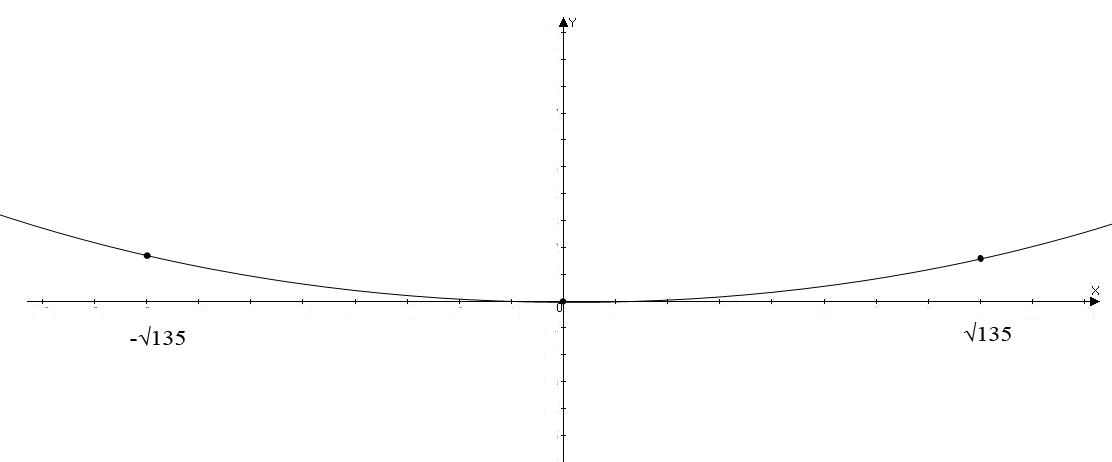
Сделаем чертёж:
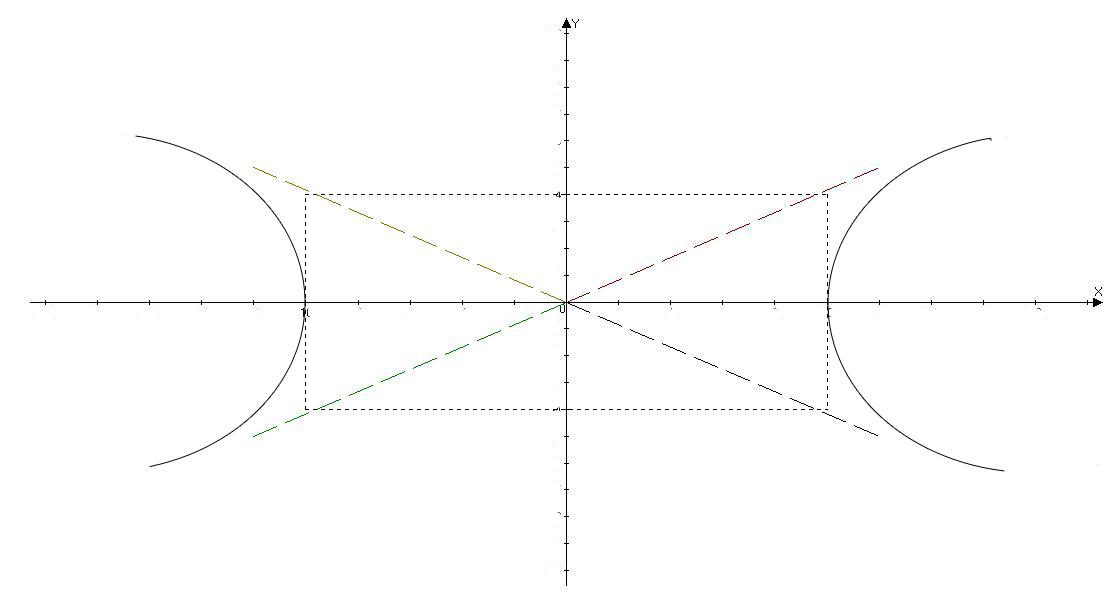
-
Ось симметрии Оy A(-45; 15)
Исходя
из условия задачи искомая парабола
имеет вид
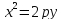 и так как точка А (-45; 15) лежит на параболе,
то координата точки должна удовлетворять
уравнению параболы
и так как точка А (-45; 15) лежит на параболе,
то координата точки должна удовлетворять
уравнению параболы
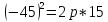
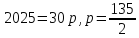
Отсюда
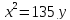
№10
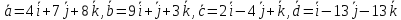
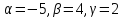
-
Найдём скалярное произведение векторов
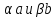 ,
так как
,
так как
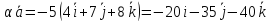
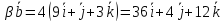 ,
,
то
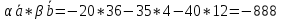
-
Найдём модуль векторного произведения
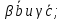
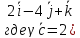
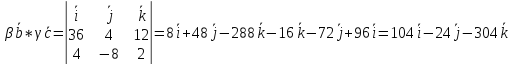
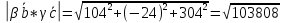
-
Проверить кол линеарность и ортогональность векторов
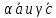 :
:
так
как
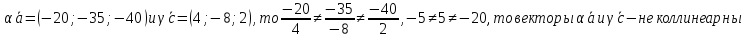
Поскольку
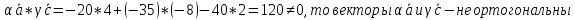
-
Вычислим определитель:
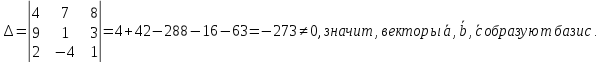
-
Найти координаты вектора
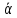 в этом базисе
в этом базисе
Пусть
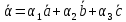
Из условия задачи
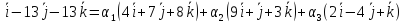
Из равенства векторов имеем:
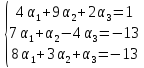
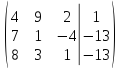
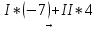
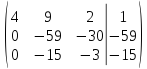
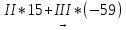
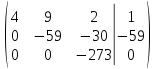
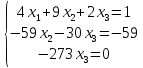
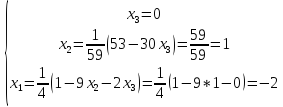
Искомое
разложение имеет вид