Высшая математика Контрольная №2 Вариант №3

№43. Доказать совместимость данной системы линейных уравнений и решить ее тремя методами:

1. по формулам Крамера,

2. методом Гаусса,

3. средствами матричного исчисления (с помощью обратной матрицы)

Решение:

Используя теорему Кронекера-Капелли исследуем данную систему на совместимость.

Основная матрица системы и расширенная матрица системы имеют вид:

А=, С=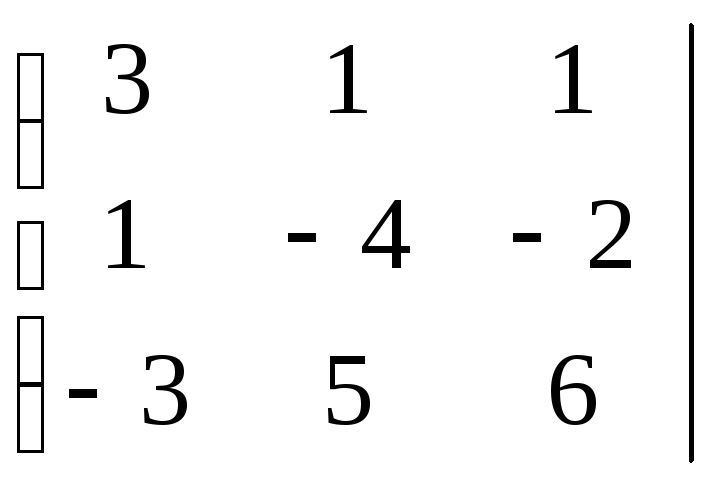

Найдем ранги матриц А и С.

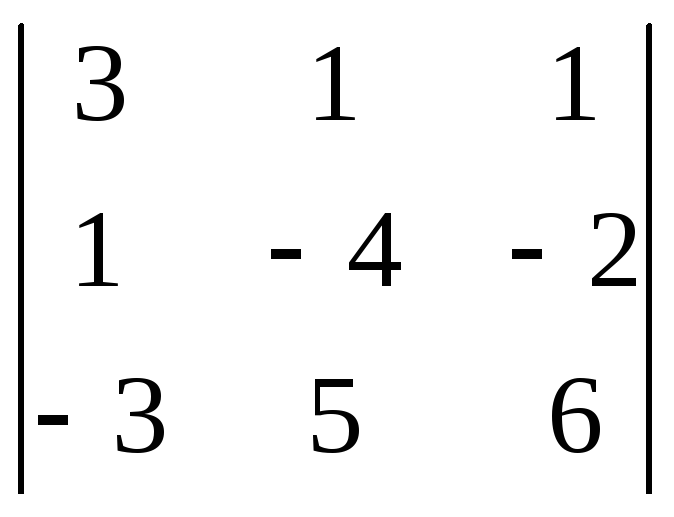==3·-1·+1·=3 (-24+10)-(6-6)+(5-12)= --49 ≠ 0 r(А)=3.

Т.к. количество неизвестных n также равно 3, то ранг расширенной матрицы С совпадает с рангом А и равен 3. След-но, по теореме Кронекера-Капелли исходная система уравнений совместна, причем т.к. r(А) = r(С). Где n=3, то система имеет единственное решение. Найдем его.

1) Формулы Крамера в нашем случае будут иметь вид:

Х_{1 =,} Х_{2 =,} Х_{3 =,}

Где ∆ = = - 49.

∆₁, ∆_2, ∆₃ – определители, которые получаются из определителя ∆ заменой соответственно 1-го, 2-го, 3-го столбца на столбец свободных членов.

Найдем ∆₁, ∆_2, ∆₃

∆₁= =21· -1· +1· =21(-24+10) - (- -96+82) + (-80+164) = -196,

∆₂= =3· -21· +1· =3(-96+82) - 21(6-6) + +(41-48) = -49,

∆₃= =3· -1· +21· =3(-164+80) –

-(41-48)+ 21(5-12) = -392.

Следовательно,

Х_{1 ===} 4_, Х_{2 ===} 1 _, Х_{3 == =} 8.

2) метод Гаусса

Выпишем расширенную матрицу системы и преобразуем ее:

(поменяем местами 1-ую и 2-ую строки)

(вычтем из 2-ой строки 1-ую, умнож. на 3, а к 3-ей строке прибавим 1-ую, умнож. на 3)

(прибавим к 3-ей строке 2-ую, умнож. на ) .

Таким образом, система принимает вид:

Из 3-го уравнения находим Х₃=8.

Подставляя Х₃ во 2-ое уравнение, находим Х₂:

13х₂+7·8=69 Х₂=1

подставляя Х₂ и Х₃ в 1-ое уравнение, найдем Х₁:

Х₁-4·1-2·8= -16 Х₁=4.

Итак, Х₁ = 4, Х₂ = 1, Х₃ = 8.

3. Матричный способ.

Т.к. ≠0, то решение системы может быть найдено по формуле:

Х = А^-1 ·b,

Где Х = , А^-1 – обратная матрица к А, b – столбец свободных членов.

А^-1 найдем по формуле

А^-1 = , где - алгебраические дополнения к элементам

а_ij матрицы А.

А₁₁ = = -14 А₂₁ = - = -1 А₃₁ = = 2

А₁₂ = - = 0 А₂₂ = = 21 А₃₂ = - = 7

А₁₃= = -7 А₂₃ = - = -18 А₃₃ = = -13

Итак,

А^-1 =

Находим решение системы:

Х = = А^-1·b = - ·= -=

= - = .

Итак, Х₁=4, Х₂=1, Х₃=8.

Ответ: (4; 1; 8).

№53. Найти общее решение системы линейных уравнений:

Решение:

Выпишем расширенную матрицу и преобразуем ее:

(вычтем из 2-ой и 3-ей строк 1-ую,умножен. соответственно на 3 и 2)

(отбросим 3-ю строку)

(прибавим к 1-ой строке 2-ую)

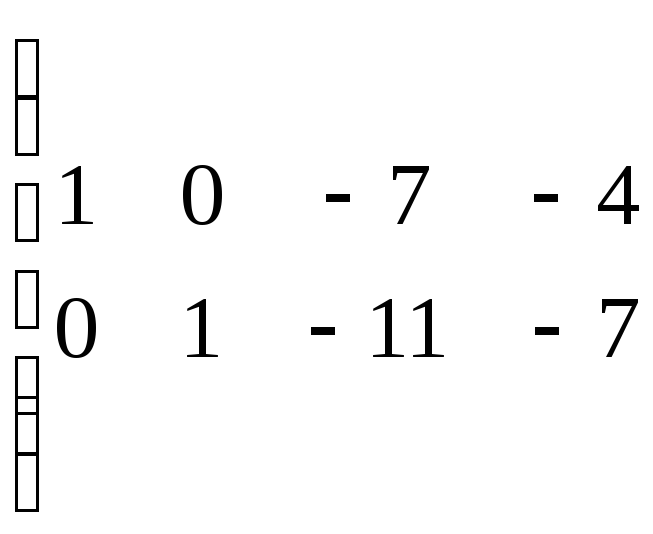
Т.к. расширенная матрица системы приведена выше к виду

то исходная система уравнений равносильна системе:

Пусть Х₃ = t₁, Х₄ = t₂, t₁, t₂ R.

Тогда общее решение системы:

Ответ:

№63.

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

Решение:

Составим характеристическое уравнение и решим его:

= 0

=(2-)·+2·+1·=(2-)(-·(2-))+2(-3(2-)+3)+(0-3) =

= - (2-)² – 6 (2-) + 6-3 = -(2-)² – 6 (2-) + 3 (2-) = (2-)·(-(2-) -6+3) =

= (2-)(²-2-3) = (2-)( -3) (+1) = 0,

₁₌ - 1_{, 2 =} 2_{, 3 =} 3_.

Т.к. все характеристические числа действительные, то собственными значениями являются:

₁₌ - 1_{, 2 =} 2_{, 3 =} 3_.

1) Найдем собственный вектор с собственным значением ₁₌ - 1_, для чего составим систему

, , , ,

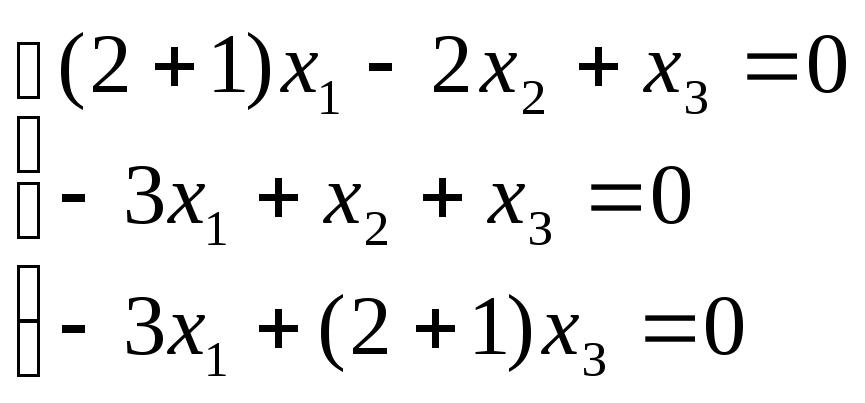
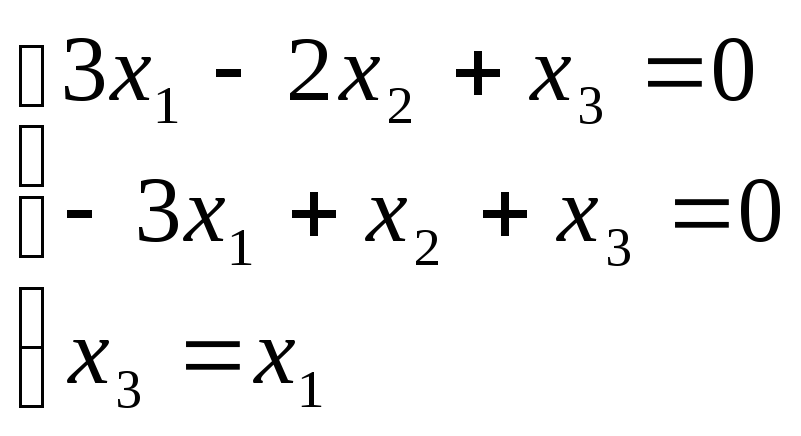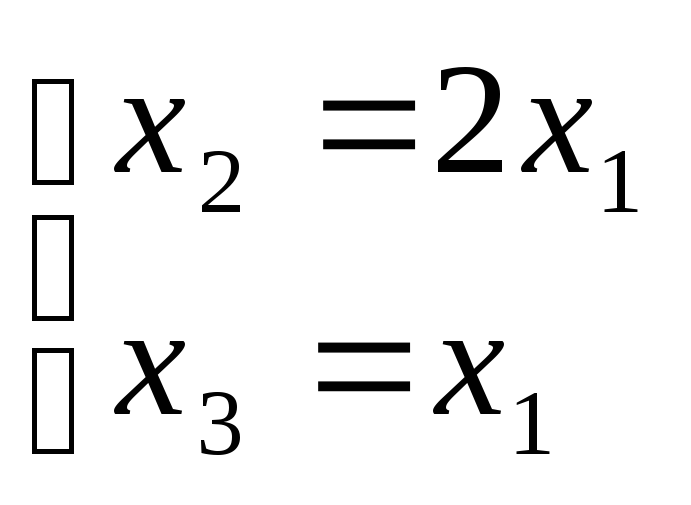, , tR.

= t (1,2,1).

2) Для _{2 =} 2 имеем:

, , ,

= t (0,1,2).

3) Для _{3 =} 3 имеем:

, , , ,

,

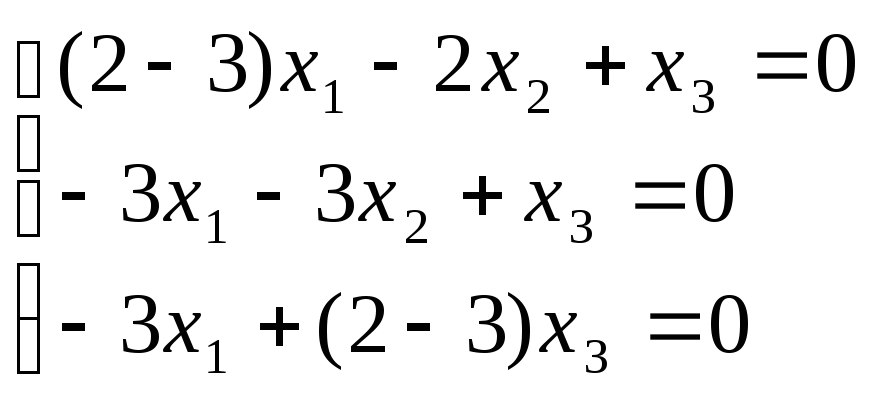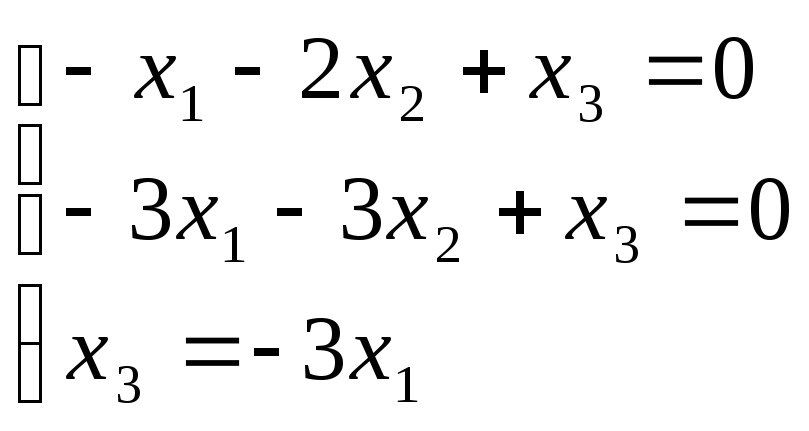= t (1,-2,-3).

Ответ: = t (1,2,1), = t (0,1,2), = t (1,-2,-3).

№73

Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка и построить ее в декартовой системе координат.

Решение:

В уравнении заданной кривой присутствует квадратичная форма следующего вида: Составим матрицу данной квадратичной формы и найдем ее собственные значения:

Для

Для

и - собственные векторы.

Формируя собственные векторы, получим:

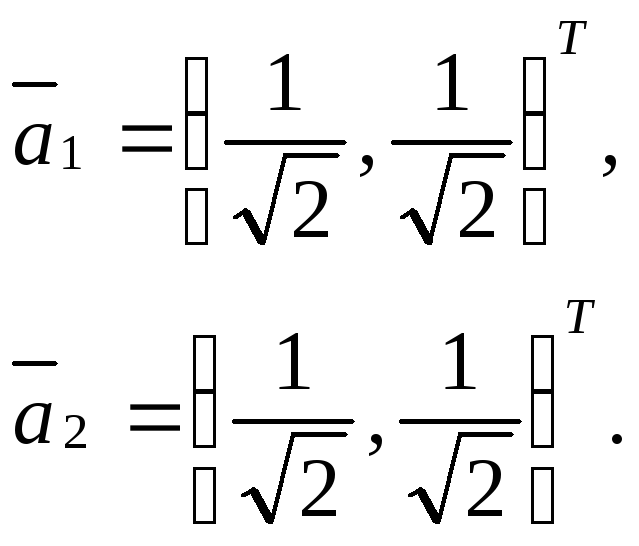
Матрица перехода T к новому базису имеет вид

В соответствии с соотношением вводим замену переменных

Подставим эти выражения в исходное уравнение:

Введя замену 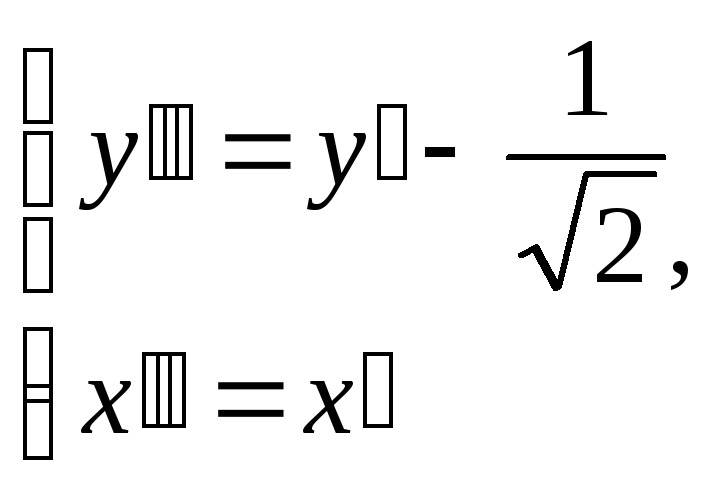получим уравнения параллельных прямых:

-