
- •1.Многочлены.
- •2. Рациональные дроби.
- •3. Понятие первообразной ф-ции и неопределенного интеграла.
- •4. Замена переменной в неопределенном интеграле.
- •5. Интегрирование по частям в неопределённом интеграле.
- •6. Интегрирование рациональных функций.
- •7. Интегрирование тригонометрических функций.
- •8. Интегрирование иррациональных функций.
- •11. Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
- •12. Замена переменных в определенном интеграле.
- •13. Интегралы от периодических, нечетных и четных ф-ций.
- •14. Вычисление площадей плоских фигур.
- •15. Вычисление длины дуги с помощью определенного интеграла.
- •17. Ни-1
- •18. Несобственные интегралы второго рода.
- •19. Понятие функции нескольких переменных. Предел функции нескольких переменных в точке, повторные пределы. Непрерывность.
- •20. Частные производные .
- •21 . Дифференцируемость функции нескольких переменных. Необходимые условия дифференцируемости. Достаточные условия дифференцируемости. Полный дифференциал.
- •22. Частные производные сложной функции. Дифференциал сложной функции. Инвариантность формы полного дифференциала.
- •23. Неявные функции и их дифференцирование.
- •24. Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
- •25. Частные производные высших порядков. Теорема о равенстве смешанных производных. Дифференциалы высших порядков. Матрица Гессе.
- •26. Формула Тейлора для функции нескольких переменных.
- •27. Локальный экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточные условия экстремума.
- •28. Условный экстремум функции нескольких переменных. Метод множителей Лагранжа. Наибольшее и наименьшее значения непрерывной функции в замкнутой области.
- •29. Интегралы по фигуре от скалярной функции, их свойства, геометрические и физические приложения.
- •30. Криволинейный интеграл первого рода.
- •36. Криволинейный интеграл второго рода, его механический смысл, скалярная форма и вычисление.
- •Скалярная форма кри-2
- •37. Формула Грина.
- •38. Условия независимости криволинейного интеграла второго рода от пути. Интегрирование полных дифференциалов.
- •39. Поверхностный интеграл второго рода, его физический смысл, скалярная форма и вычисление..
- •40. Скалярные поля. Производная скалярного поля по направлению. Градиент.
- •41. Векторные поля. Поток векторного поля. Дивергенция.
- •42. Циркуляция и ротор векторного поля.
- •43. Операторы Гамильтона и Лапласа.
- •44 Потенциальное векторное поле и его свойства.
- •45.Соленоидальное векторное поле. Гармоническое векторное поле.
36. Криволинейный интеграл второго рода, его механический смысл, скалярная форма и вычисление.
Механический смысл КРИ-2:
![]() (М)
– вектор силы;L=AB;
Работа силы по перемещению вдольL.
Если
(М)
– вектор силы;L=AB;
Работа силы по перемещению вдольL.
Если![]() (М)
– переменная сила, аAB–
кривая, то:
(М)
– переменная сила, аAB–
кривая, то:![]() -
настолько малы, что перемещение на
кусочек по направлению совпадает с
единичным касательным вектором.
-
настолько малы, что перемещение на
кусочек по направлению совпадает с
единичным касательным вектором.![]() -произвольная
точка.
-произвольная
точка.![]() (
(![]() )
– постоянная сила.
)
– постоянная сила.![]() =(
=(![]() (
(![]() ),
),![]() )=(
)=(![]() (
(![]() ),
),![]() )
)![]()
![]()
!!! С механической точки зрения КРИ-2 представляет собой работу силы вдоль линииL.
Скалярная форма кри-2

Вычисление КРИ-2
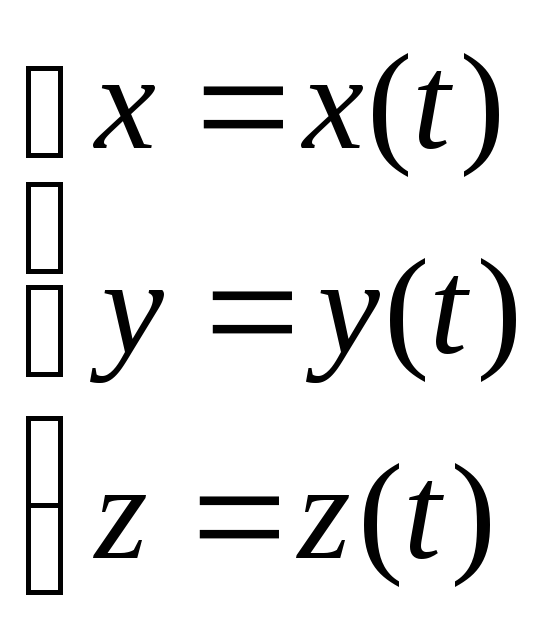 ,
,
![]()
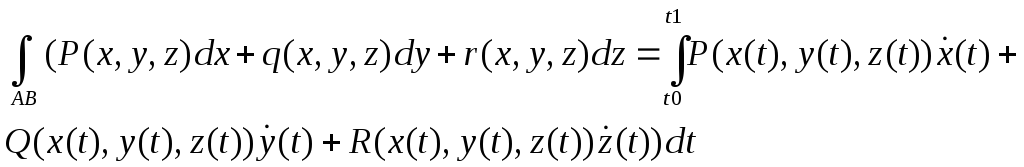
Вывод: в общем случае КРИ-2 зависит от пути интегрирования.
37. Формула Грина.
Область наз. односвязной если в ней любой замкнутый контур может быть стянут в точку с помощью непрерывной деформации, при к-й не границы области не пересекаютя.
Область D наз. односвяз., если каков бы ни был замкн. контур l , лежащий внутри этой области, ограниченная этим контуром конечн. часть пл-ти целиком принадл. D.
Порстая область: замкн. пл-ть D (обл. вместе с её границами) – её можно разбить на конечное число как y- так и x- трапецивидных областей.
Например: круг, прямоугольник, кольцо.
Теор. Грина: пусть
P(x,y),
Q(x,y)
и
![]() и
и![]() непрерывны в простой областиD
тогда
непрерывны в простой областиD
тогда
![]()
где L – граница области D, к-я обходится в положительном направлении.
Док-во
Предположим D – односвяз. область, огр. L – полож. ориентир. Предположим, что оюл. D такова, что прямые параллельн. осям пересекают ее не более, чем в 2-х точках.

Для I2 – аналогично.
Формула Грина имеет место для любой простой области.
Если контур обходится в обратном направлении, то перед двойным интегралом ставится «-».
38. Условия независимости криволинейного интеграла второго рода от пути. Интегрирование полных дифференциалов.
Пусть ф-ции P(x,y),Q(x,y) и их частные производные dP/dy, dQ/dx непрерывны, замкнуты, ограничены односвязной областью Д, тогда следующие 4 условия эквивалентны:
1)
![]() ,
гдеL
– любой замкнутый контур Д.
,
гдеL
– любой замкнутый контур Д.
2)![]() не
зависит от путиAB.
не
зависит от путиAB.
3) Pdx+Qdy=dU, U – однозначная ф-ция, определенная в области Д. \
4) dP/dy=dQ/dx в области Д.
Доказательство:
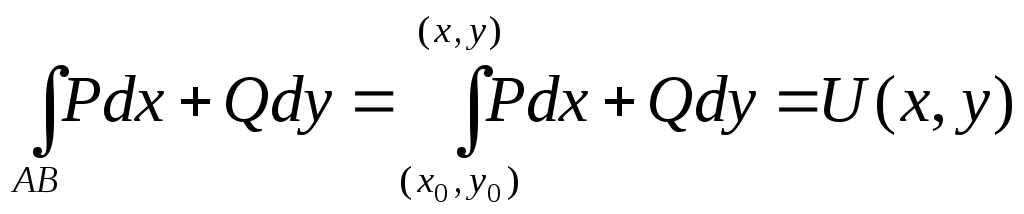
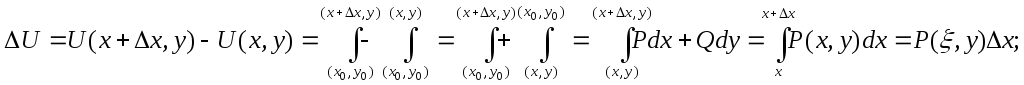
где
![]() .
.
Т.к. у ф-ции U существуют непрерывные частные произодные, то она дифиренцируема.
![]()
Нахождение ф-ции по ее полному дифференциалу.
Первый способ:
U(x,y)-?; dU=Pdx+Qdy; Pdx+Qdy*dQ/dx=dP/dy
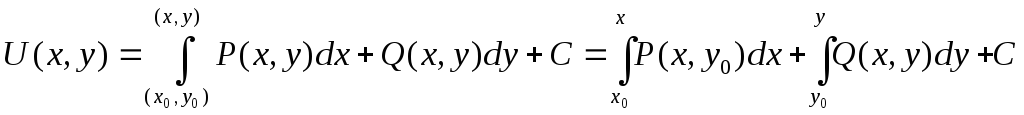
Второй способ:
![]() ;
;
![]()
![]()
{![]() ;
;![]() }
;
}
;![]()
![]() не зависит от пути.
не зависит от пути.
39. Поверхностный интеграл второго рода, его физический смысл, скалярная форма и вычисление..
Пусть ф-ции P(x,y),Q(x,y) и их частные производные dP/dy, dQ/dx непрерывны, замкнуты, ограничены односвязной областью Д, тогда следующие 4 условия эквивалентны:
1)
![]() ,
гдеL
– любой замкнутый контур Д.
,
гдеL
– любой замкнутый контур Д.
2)![]() не
зависит от путиAB.
не
зависит от путиAB.
3) Pdx+Qdy=dU, U – однозначная ф-ция, определенная в области Д. \
4) dP/dy=dQ/dx в области Д.
Доказательство:
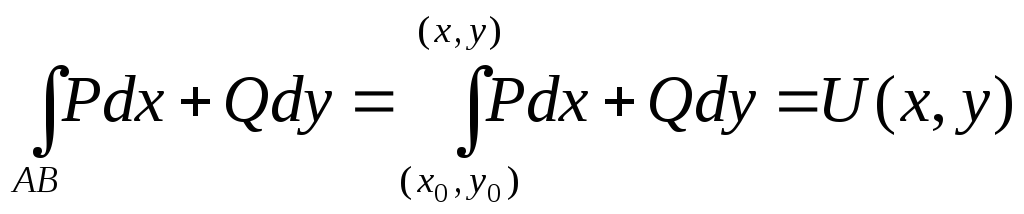
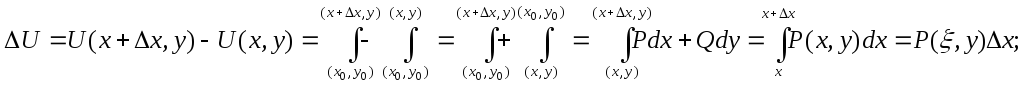
где
![]() .
.
Т.к. у ф-ции U существуют непрерывные частные произодные, то она дифиренцируема.
![]()
Нахождение ф-ции по ее полному дифференциалу.
Первый способ:
U(x,y)-?; dU=Pdx+Qdy; Pdx+Qdy*dQ/dx=dP/dy
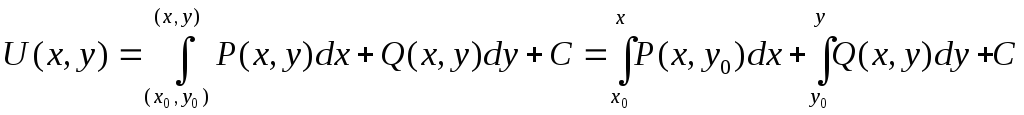
Второй способ:
![]() ;
;
![]()
![]()
{![]() ;
;![]() }
;
}
;![]()
![]() не зависит от пути.
не зависит от пути.
40. Скалярные поля. Производная скалярного поля по направлению. Градиент.
Пусть V
– некоторая область в пространстве.
Говорят, что в этой области задано
скалярное поле, если каждой т.
![]() поставлено
в соответствие некоторое числоU(M)
(пример – поле температур, освещенности).
Скалярное поле не зависит от выбора
системы координат. Поверхность или
линия, на которой U(M)
принимает постоянное значение называется
поверхностью уровня скалярного поля.
поставлено
в соответствие некоторое числоU(M)
(пример – поле температур, освещенности).
Скалярное поле не зависит от выбора
системы координат. Поверхность или
линия, на которой U(M)
принимает постоянное значение называется
поверхностью уровня скалярного поля.
Пусть U(M)
– некоторое скалярное поле.
![]() -
единственный фиксированный вектор.
-
единственный фиксированный вектор.![]() -фиксированая
точка.
-фиксированая
точка.![]() ;
;![]() ;
;![]()
Если
![]() ,
то он называется производной скалярного
поляU(M)
по направлению
,
то он называется производной скалярного
поляU(M)
по направлению
![]() в точке
в точке![]() .
.![]()
lnH-скорость
изменения ф-ции U(m)
по направлению
![]() в точке
в точке![]() .
.
![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;
![]()
![]()
![]()
![]() ;
;
![]() ;
;![]() ;
;
![]() принимает наибольшее
значение при
принимает наибольшее
значение при
![]() ,
т.е. в направлении вектораgradU
в т.
,
т.е. в направлении вектораgradU
в т.
![]()
gradU указывает направление наибольшего роста поля в данной точке. | gradU| - скорость роста ф-ции U в данном направлении. Вектро gradU не зависит от выбора системы координат. Grad направлен по поверхности уровня в данной точке.
