
- •1.Многочлены.
- •2. Рациональные дроби.
- •3. Понятие первообразной ф-ции и неопределенного интеграла.
- •4. Замена переменной в неопределенном интеграле.
- •5. Интегрирование по частям в неопределённом интеграле.
- •6. Интегрирование рациональных функций.
- •7. Интегрирование тригонометрических функций.
- •8. Интегрирование иррациональных функций.
- •11. Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
- •12. Замена переменных в определенном интеграле.
- •13. Интегралы от периодических, нечетных и четных ф-ций.
- •14. Вычисление площадей плоских фигур.
- •15. Вычисление длины дуги с помощью определенного интеграла.
- •17. Ни-1
- •18. Несобственные интегралы второго рода.
- •19. Понятие функции нескольких переменных. Предел функции нескольких переменных в точке, повторные пределы. Непрерывность.
- •20. Частные производные .
- •21 . Дифференцируемость функции нескольких переменных. Необходимые условия дифференцируемости. Достаточные условия дифференцируемости. Полный дифференциал.
- •22. Частные производные сложной функции. Дифференциал сложной функции. Инвариантность формы полного дифференциала.
- •23. Неявные функции и их дифференцирование.
- •24. Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
- •25. Частные производные высших порядков. Теорема о равенстве смешанных производных. Дифференциалы высших порядков. Матрица Гессе.
- •26. Формула Тейлора для функции нескольких переменных.
- •27. Локальный экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточные условия экстремума.
- •28. Условный экстремум функции нескольких переменных. Метод множителей Лагранжа. Наибольшее и наименьшее значения непрерывной функции в замкнутой области.
- •29. Интегралы по фигуре от скалярной функции, их свойства, геометрические и физические приложения.
- •30. Криволинейный интеграл первого рода.
- •36. Криволинейный интеграл второго рода, его механический смысл, скалярная форма и вычисление.
- •Скалярная форма кри-2
- •37. Формула Грина.
- •38. Условия независимости криволинейного интеграла второго рода от пути. Интегрирование полных дифференциалов.
- •39. Поверхностный интеграл второго рода, его физический смысл, скалярная форма и вычисление..
- •40. Скалярные поля. Производная скалярного поля по направлению. Градиент.
- •41. Векторные поля. Поток векторного поля. Дивергенция.
- •42. Циркуляция и ротор векторного поля.
- •43. Операторы Гамильтона и Лапласа.
- •44 Потенциальное векторное поле и его свойства.
- •45.Соленоидальное векторное поле. Гармоническое векторное поле.
17. Ни-1
Пусть f(x) определена на
![]() и инт на
и инт на![]()
![]() ;
;![]() ,
т.е.
,
т.е.![]()
Пусть
![]() .
Если этотlimсуществует
и конечен, то говорят, что НИ-1 сходится.
Если не существует или бесконечен, то
расходится.
.
Если этотlimсуществует
и конечен, то говорят, что НИ-1 сходится.
Если не существует или бесконечен, то
расходится.
![]() ;
;
Аддитивность : Если
 сходится, то
сходится, то ,
, ;
;
Линейность: Если
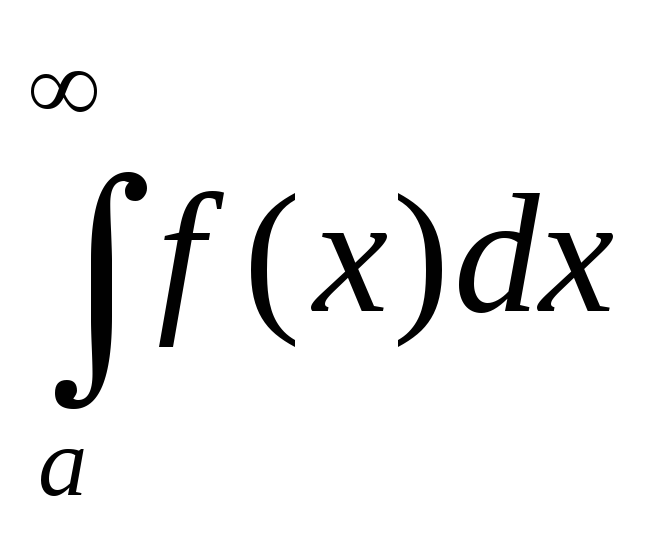 сходится и
сходится и сходится, то
сходится, то сходится и
сходится и
![]()
Вычисление и преобразование НИ-1.
Если f(x)
непрерывна на![]() иF– какая-то первообразная
для ф-цииf(x),
то
иF– какая-то первообразная
для ф-цииf(x),
то
![]()
Интегрирование по частям.: ЕслиU,V– непрер.
Диф-мы ф-ции на![]() ,
то
,
то![]()
Исследование на сходимость.
Т1: Пусть ф-ции f(x)
иg(x)![]() ,
тогда если
,
тогда если![]() и
и![]() ,
то
,
то
![]()
![]()
сходится
![]() сходится
сходится
расходится
![]() пасходится
пасходится
Предельный признак сравнения для НИ-1.
Т2: Пусть![]() ,
,![]()
![]() ;
;![]() ,
тогда если
,
тогда если![]() конечный
конечный![]() ,
то
,
то![]() и
и![]() сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
При k=1![]() при
при![]()
Т3: Если
![]() и
и![]() сходится, то
сходится, то![]() сходится.
сходится.
Определение:
![]() называется абсолютно сходящимся, если
сходится
называется абсолютно сходящимся, если
сходится![]() .
.
Если
![]() расходится, а
расходится, а![]() сходится, от
сходится, от![]() -
неабсолютно (условно) сходящийся
-
неабсолютно (условно) сходящийся
Главное значении.
 ,
,![]() ,
Если
,
Если![]() и сходится, то
и сходится, то![]() и
и![]()
18. Несобственные интегралы второго рода.
f(x) определена
на [a,b);![]() ;
;![]() ,
т.е.
,
т.е.![]()
![]() называется НИ-2 и обозначается
называется НИ-2 и обозначается![]()
Если этот Limсуществует
и конечен, то говорят, что![]() сходится.
Если он не сущ-т или бесконечен, то НИ-2
расходится.
сходится.
Если он не сущ-т или бесконечен, то НИ-2
расходится.
Свойства НИ-2.
{Аналогично НИ-1.}
Аддитивность
Если
![]() сходится, то
сходится, то![]() ,
,![]() ;
;![]()
Линейность
Если
![]() сходится и
сходится и![]() сходится, то
сходится, то сходится и
сходится и
![]()
Вычисление и преобразование НИ-2.
Формула Ньютона-Лейбница.
f(x) – непрерывна на [a.b);F(X) - некоторая первообразная.
![]()
![]()
![]()
![]()
Интегрирование по частям.
Если U(x) иV(x) непр. И
диф-мы на [a,b),
то![]()
Исследование на сходимость.
{Аналогично НИ-1.}
Главное значении НИ-2.
f(x) определено
на![]()

Определение:
![]()
19. Понятие функции нескольких переменных. Предел функции нескольких переменных в точке, повторные пределы. Непрерывность.
Опр. т. А наз.
пределом посл-ти (Mn)
если
![]() для любого Е(эпсилон) сущ.N-N(E);
любое n>=N(E)
=> p(Mn,A)
< E;
для любого Е(эпсилон) сущ.N-N(E);
любое n>=N(E)
=> p(Mn,A)
< E;
![]() ;
;![]() (число)
(число)
(x1, x2, …,xm)-независимые переменные.
Опр по Коши: число
b
наз пределом ф-ии u=f(M)
в т. А (при
![]() ),
если для любого Е > 0 сущ.
),
если для любого Е > 0 сущ.![]() ,
для любого
,
для любого![]()
Опр по Гейне: число
b
наз пределом посл-ти ф-ии u=f(M)
в т. А, если для любого (Mn),
![]()
 A(a1,
a2,…,
am)
A(a1,
a2,…,
am)
Теор.
Если
сущ.
![]() и
сущ.
и
сущ.![]() ,
то сущ.
,
то сущ.![]() ,
причем
,
причем![]()
Опр. u=f(M)
наз. непрерывной в т. А, если
![]()
M(x1,
x2,
…,xn)
![]() ;
;
![]() …
…
![]() ;
A(a1,
a2,
…,an)
;
A(a1,
a2,
…,an)
![]()
Опр2. u=f(M)
наз. непрерывной в т. А, если

Точка в к-й ф-я не определена или не является непрерывной, наз. точками разрыва этой ф-ии.
20. Частные производные .
Частная производная
ф-ции
![]() в
точке
в
точке![]() по
переменнойx
называется
по
переменнойx
называется
![]() ,
если он
,
если он
![]() .
.
![]() ;
;
![]() ;
;
![]() непрерывна
непрерывна
![]()
![]() имеет частные
производные в т. А,В
имеет частные
производные в т. А,В
![]() непрерывна
в т. А,В.
непрерывна
в т. А,В.
21 . Дифференцируемость функции нескольких переменных. Необходимые условия дифференцируемости. Достаточные условия дифференцируемости. Полный дифференциал.
![]() ;
;
![]() ;
;![]()
![]() ;
;
![]()
Ф-ция
![]() называется
диф-м в точке
называется
диф-м в точке![]() если ее полное приращение
если ее полное приращение![]() может быть представлено в виде
может быть представлено в виде![]() ,
где
,
где![]() ,
А,В – числа.
,
А,В – числа.
Теорема: Если
![]() диф в точке
диф в точке![]() ,
то
,
то![]() непрерывна в этой точке.
непрерывна в этой точке.
Док-во:
![]() -диф-ма
в т.
-диф-ма
в т.![]()
![]() ;
;

 -
непрерывна в точке
-
непрерывна в точке
![]()
Теорема (необходимое
условие диф): Если
![]() диф в точке
диф в точке![]() ,
то
,
то![]()
![]()
Док-во:
![]() ;
;![]() ;
;
![]()
![]()
![]()
Теорема (достаточное
условие диф): Если
![]() имеет
частные производные в некоторой
окрестности т.
имеет
частные производные в некоторой
окрестности т.![]() ,
непрерывна в самой точке
,
непрерывна в самой точке![]() ,
то она диф. В точке
,
то она диф. В точке![]() .
.
Если
![]() дифф. В т.
дифф. В т.![]() ,
то главная линейная, относительно
приращения аргумента, часть его полного
приращения называется полным диффиринциалом
ф-ции
,
то главная линейная, относительно
приращения аргумента, часть его полного
приращения называется полным диффиринциалом
ф-ции![]() в
т.
в
т.![]()
![]() ;
;
![]()
![]() ;
;
![]() ;
;![]()
