ВМ Контрольна 1 вариант 8

Белорусский государственный университет информатики и радиоэлектроники

Факультет заочного и дистанционного обучения

Контрольная работа №1

по математике

8. Даны четыре вектора (-2, 1, 7), (3, -3, 8), (5, 4, -1) и (18, 25, 1) в некотором базисе. Показать, что векторы , , образуют базис, и найти координаты вектора в этом базисе.

, , образуют базис, если λ₁+ λ₂+ λ₃=0 и => λ1= λ2= λ3=0.

λ₁(-2; 1; 7)+ λ₂(3; -3; 8)+ λ₃(5;4;-1)=(0; 0; 0)

,

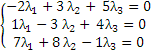∆ = ((-2) · (-3) · (-1)+1·8·5+7·3·4) – (5·(-3) ·7+(-2) ·4·8+(-1) ·3·1)=290≠0

Т.к. 290≠0, то система имеет только тривиальные решения =>, , образуют базис и может быть разложен единственным образом.

λ₁+ λ₂+ λ₃=

Решим систему методом Гаусса:

~~

-580 λ₃=-2900 => λ₃ = 5

3λ₂-13λ₃=-68 => λ₂ = -1

-2λ₁+3λ₂+5λ₃=18 => λ₁ = 2

Ответ: (2; -1; 5)

18. Даны координаты вершин пирамиды: A₁ (6; 1; 1), A₂ (4; 6; 6), A₃ (4; 2; 0), A₄ (1; 2; 6). Найти: 1) длину ребра А₁А₂; 2) угол между ребрами А₁А₂ и А₁А₄; 3) угол между ребром А₁А₄ и гранью А₁А₂А₃; 4) площадь грани А₁А₂А₃; 5) объём пирамиды; 6) уравнения прямой А₁А₂; 7) уравнение плоскости А₁А₂А₃; 8) уравнения высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертёж.

1. Длина ребра А₁А₂:

Определим координаты вектора :

= (x₂-x₁; y₁-y₂; z₁-z₂)=(4-6; 6-1; 6-1)=(-2; 5; 5)

Вычислим модуль вектора т.е. его длину:

||===

2. Угол между ребрами и :

Координаты вектора :

=(x₂-x₁; y₁-y₂; z₁-z₂)= (1-6; 2-1; 6-1)=(-5; 1; 5)

Длина вектора :

||===

Скалярное произведение векторов и :

(, )=(x₂·x₁+y₁·y₂+z₁·z₂)=((-2)·(-5)+5·1+5·5)=10+5+25=40

=arccos ≈40,3°

3. Угол между ребром А₁А₄ и гранью А₁А₂А₃:

=(-2; 5; 5)

= (x₂-x₁; y₁-y₂; z₁-z₂)=(4-6; 2-1; 0-1)=(-2; 1; -1)

= (-5; 1; 5)

====(-10; -12; 8)

≈38,5°

4. Площадь грани А₁А₂А₃:

5. Объём пирамиды:

=(-2; 5; 5); = (2; 1; -1); = (-5; 1; 5)

V== (-2·1·5+5·(-1) ·(-5)+(-2) ·1·5-(5·1·(-5)+(-2) ·(-1) ·1+(-2) ·5·5))==13

6. Уравнение прямой А₁А₂:

A₁ (6; 1; 1), A₂ (4; 6; 6)

7. Уравнение плоскости А₁А₂А₃:

A₁ (6; 1; 1), A₂ (4; 6; 6), A₃ (4; 2; 0)

А₁А₂А₃:

-10(х-6)-12(y-1)+8(z-1)=0

-10x+60-12y+12+8z-8=0

-10x-12y+8z+64=0

5x+6y-4z-32=0

8. Уравнения высоты, опущенной из вершины А₄ на грань А₁А₂А₃:

А₁А₂А₃: 5x+6y-4z-32=0

; (5; 6; -4)

A₄ (1; 2; 6)

9

A₄

. Чертеж:

A₂

θ

α

A₁

A₃

28. Вычислить координаты вершин ромба, если известны уравнения двух его сторон 2x-y+4=0 и 2x-y+10=0 и уравнение одной из его диагоналей x+y+2=0.

АВ: 2x-y+4=0, DC: 2x-y+10=0, АС: x+y+2=0

B

O

A C

D

АВ АС в т.А:

2x-(-x-2)+4=0

2x+x+2+4=0

3x+6=0

x=-6:3=-2; y=-2-2=-4 => т.А (-2; -4)

АC DС в т.C:

2x+x+2+10=0

3x+12=0

x=112:3=-4; y=-4-2=-6 => т.С (-4; -6)

т.О (-3; -5)

(1; 1)

BD: ; x+3=y+5; x-y-2=0

BD АB в т.B

2x-x+2+4=0

x=-6; y=-6-2=-8 => т.В (-6; -8)

BD DС в т.C

2x-x+2+10=0

x+12=0

x=-12; y=-12-2=-14 => т.D (-12; -14) Ответ: А(-2; -4), В(-6; -8), С(-4; -6), D(-12; -14)

38. Построить на плоскости область решений системы линейных неравенств.

Область решений системы линейных неравенств заштрихована на рисунке.

0

х

y

48. Составить уравнение линии, каждая точка которой равноудалена от точки A(4,2) и от оси ординат.

Гипербола – плоская кривая второго порядка, каждая точка которой равноудалена от директрисы (прямая перпендикулярная к оси симметрии параболы) и от фокуса (точка, расположенная на оси симметрии параболы).

Из условия задачи следует, что фокус находится в т.А(4,2), а директриса совпадает с осью ординат (y=0). Ось симметрии пересекает ось ординат в т.О(0; 2) (т.к. фокус А(4; 2) лежит на оси симметрии, а сама ось перпендикулярна директрисе).

Уравнение параболы: y²=2px, p>0, следовательно, необходимо найти параметр р и смещение вершины параболы (т.е. ее координаты).

По свойству параболы параметр р – есть расстояние между фокусом А(4;2) и точкой О(0; 2).

|p|==4

Вершина параболы лежит между фокусом А(4; 2) и точкой О(0; 2). Используя это свойство, найдем координаты вершины параболы:

т.C (2; 2)

Подставим полученные результаты в уравнение параболы:

(y-2)²=2·4·(x-2), (y-2)²=8(x-2)

Х

y

p