Контрольная работа №12 (4 часть) 5 вариант
.doc№1
561-570.
Разложить данную периодическую функцию
с периодом 2
в ряд Фурье на отрезке [-,].
Построить график суммы ряда, а также
графики первых частичных сумм
На отрезке [-,]
функция задана формулой.
565. 
Решение
Найдем коэффициенты Фурье данной функции:
Т.к. функция f(x) – нечетная, то коэффициенты ее ряда Фурье аn = 0.
,
.
Ряд
Фурье функции
:
в нашем случае будет иметь вид:
.
Т.к.
функция
непрерывна на интервале
,
то ряд Фурье сходится к функции в каждой
точке этого интервала. Поэтому знак «~»
можно заменить знаком «=», для
.
В точках
и
ряд сходится к среднему арифметическому
односторонних пределов функции в этих
точках, т.е.
.
Построим
график суммы ряда
.
Построим графики частичных сумм ряда.
№2
571-580. Доопределяя необходимым образом, заданную в промежутке (0, а) функцию f(х), получить для нее: а) ряд Фурье по синусам; б) ряд Фурье по косинусам.
575. 
Решение
а)
Доопределим функцию
до нечетной функции
.
Т.к. функция g(x) – нечетная, то коэффициенты ее ряда Фурье аn = 0. Найдем
.
Тогда ряд Фурье по синусам функции g(x) будет иметь вид:
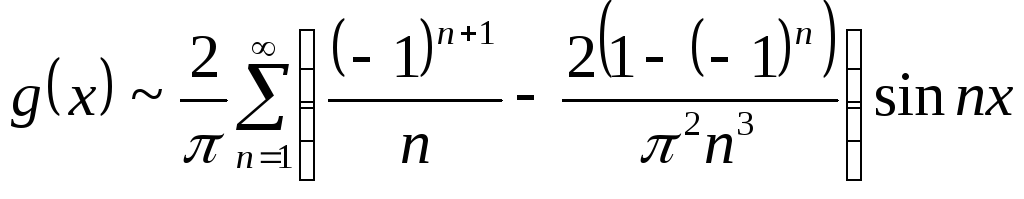
б)
Доопределим функцию
до четной функции естественным образом:
.
Т.к. функция f(x) –четная, то коэффициенты ее ряда Фурье bn = 0. Найдем
;
.
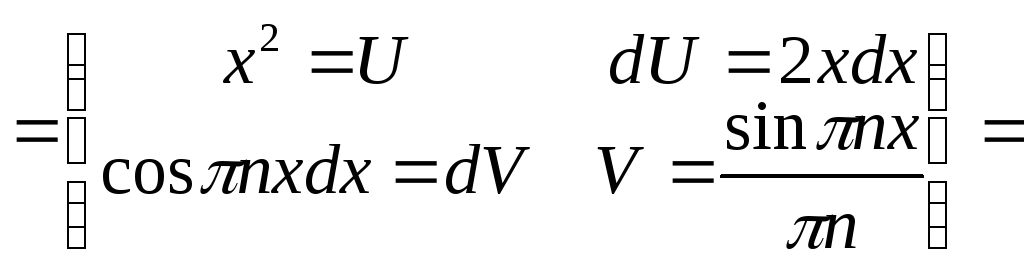
(n = 1, 2, …).
Тогда ряд Фурье по косинусам функции f(x) будет иметь вид:
№3
581-590. Найти комплексную форму ряда Фурье периодической с периодом 2l функции f(х) и найти сумму полученного ряда в точке l, если:
585. 
Решение
Найдем коэффициенты Фурье данной функции:
Ряд
Фурье функции
:
в
нашем случае будет иметь вид:
В
точке
периодическая с периодом
функция
равная
является непрерывной.
Поэтому
ряд Фурье этой функции сходится в этой
точке к значению функции
в этой точке, т.е.
№4
591-596. Найти спектральную плотность S(ω) непериодического сигнала S(t), заданного формулой:
595. 
Решение
Спектральную плотность S(ω) непериодического сигнала S(t) найдем по формуле преобразования Фурье:
№5
601-610.
Методом Фурье найти уравнение u=u(x,t)
формы однородной струны для любого
момента t, если струна закреплена на
концах х=0
и х=l
и в начальный момент t=0
форма струны и скорость точки струны с
абсциссой х
определяются соответственно заданными
функциями
605.
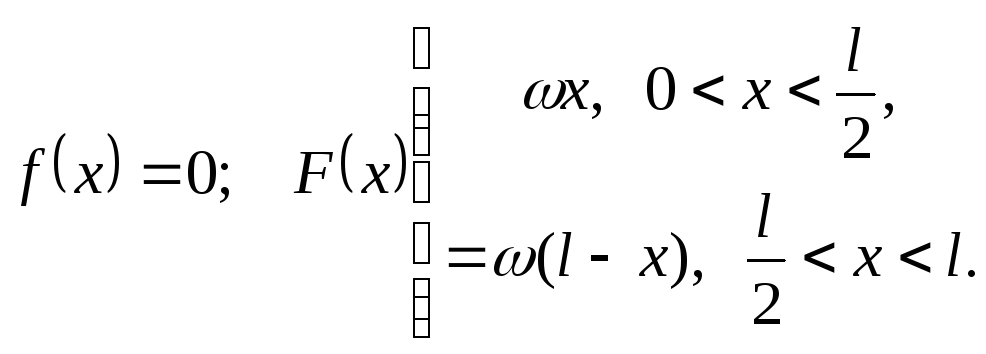
Решение
Уравнение колебания струны имеет вид:
.
Его
решение будем искать в виде
при граничных условиях:
Тогда X(0) = X(l) = 0.
Подставим решение в исходное уравнение:
.
Т.к. левая часть последнего уравнения зависит только от t, а правая только от х, то заключаем, что
.
Решаем
дифференциальное уравнение
.
Составим для него характеристическое
уравнение
.
Чтобы удовлетворить начальным условиям
X(0)
=
X(l)
= 0
необходимо, чтобы
.
Тогда общее решение этого дифференциального
уравнения будет иметь вид:
.
Тогда
;
Таким образом, функция Х имеет вид:
Аналогично находится функция T(t):
Все решения исходного дифференциального уравнения, удовлетворяющие граничным условиям, можно записать в виде:
Окончательно решение уравнения колебаний струны можно записать в виде:
где
=
Таким образом, окончательное решение уравнения колебаний струны можно записать в виде:
