BM часть 2. Контрольная работа №6. Вариант №8
.doc
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра программного обеспечения информационных технологий
Факультет НиДО
Специальность ПОИТ
Контрольная работа № 6
по дисциплине «Высшая математика»
Вариант № 8
Выполнил студент: ********
группа ******
Зачетная книжка № ******-**
Электронный адрес ******@****.***
Минск 2011
Задача 268
Найти неопределенные интегралы (результаты в случаях “а” и “б” проверить дифференцированием).
а)
б)
в)
г)
д)
Решение:
а)
Упростим подынтегральное выражение, используя формулу
,
и применим метод замены переменной.
Проверим результат дифференцированием:
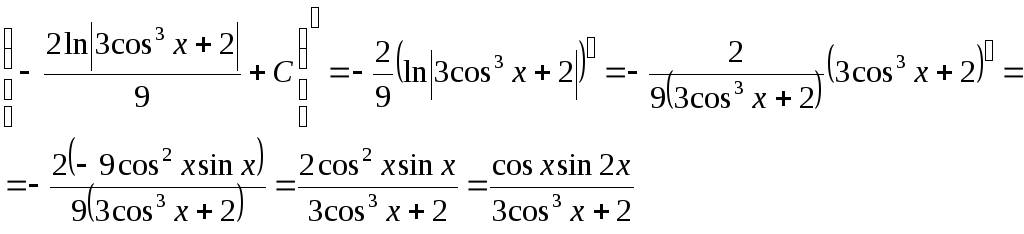
б)
Применим метод интегрирования по частям:
Проверим результат дифференцированием:
в)
Подынтегральной функцией является неправильная рациональная дробь (старшая степень многочлена в числителе равна старшей степени многочлена в знаменателе), поэтому запишем ее в виде суммы многочлена и правильной рациональной дроби
Правильную рациональную дробь разложим в сумму простейших дробей с неопределенными коэффициентами.
Найдем коэффициенты этого разложения
г)
д)
Упростим подынтегральное выражение, используя формулы
и
,
и применим метод замены переменной.
Задача 278
Вычислить определенный интеграл. Окончательный результат представить в виде приближенного числа.
Решение:
Задача 288
Вычислить несобственный интеграл или доказать его расходимость.
а)
б)
Решение:
а)
Подынтегральная функция непрерывна и
интегрируема на
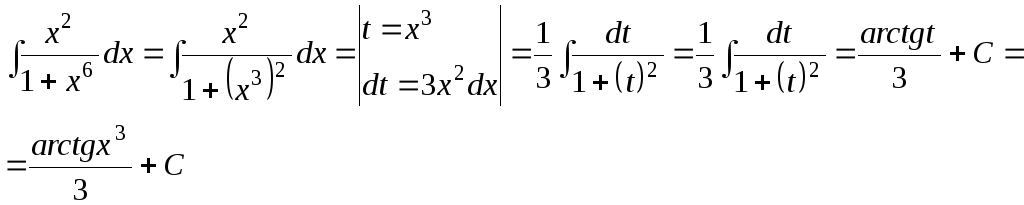
Интеграл сходится
б)
Подынтегральная функция терпит
бесконечный разрыв в точке
Интеграл расходится
Задача 298
Вычислить длину полукубической параболы
от точки
до точки
.
Решение:
Т.к. кривая
является графиком полукубической
параболы
и
непрерывна на
,
то кривая
спрямляема, и ее длина вычисляется по
формуле:
