
Часть 1. Контрольная. вариант 28
.docБЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра программного обеспечения информационных технологий
Факультет ФНиДО
Специальность ПОИТ
Контрольная работа № 1
по дисциплине «Высшая математика»
часть 1
Вариант № 28
Выполнил студент: Жукович Игорь Сергеевич
группа 291003
Студенческий билет № 2910028
Контрольная работа № 1. Основы векторной алгебры и аналитической геометрии
Задача 1 (8)
Даны четыре вектора
![]() ,
,
![]() ,
,
![]() и
и
![]() ,
заданные в декартовой системе координат.
Требуется: 1) вычислить скалярное
произведение
,
заданные в декартовой системе координат.
Требуется: 1) вычислить скалярное
произведение
![]() ;
2) вычислить векторное произведение
;
2) вычислить векторное произведение
![]() ;
3) показать, что векторы
;
3) показать, что векторы
![]() образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
![]() в этом базисе.
в этом базисе.
Решение
1) Найдем вектор
![]() для этого умножим координаты вектора
для этого умножим координаты вектора
![]() на 2 и от полученного вектора
на 2 и от полученного вектора
![]() вычтем вектор
вычтем вектор
![]() .
В результате вычитания получим
.
В результате вычитания получим
![]()
Так как скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат, то
![]() .
.
2) По аналогии с
пунктом 1 найдем вектор
![]() .
Тогда векторное произведение
.
Тогда векторное произведение
![]() найдем по формуле
найдем по формуле
 :
: 
3) Базисом в
пространстве
![]() являются любые три некомпланарных
вектора. Условием компланарности трех
векторов, заданных в декартовой системе
координат, является равенство их
смешанного произведения нулю. Отсюда
находим:
являются любые три некомпланарных
вектора. Условием компланарности трех
векторов, заданных в декартовой системе
координат, является равенство их
смешанного произведения нулю. Отсюда
находим:

![]() .
.
Значит, векторы
![]() некомпланарны и образуют базис. Составим
систему уравнений в координатном виде
некомпланарны и образуют базис. Составим
систему уравнений в координатном виде
 ,
где
,
где
![]() координаты вектора
координаты вектора
![]() в базисе
в базисе
![]() ,
и найдем
,
и найдем
![]() .
.
Определитель
![]() найден выше:
найден выше:
![]() .
.
 ;
;
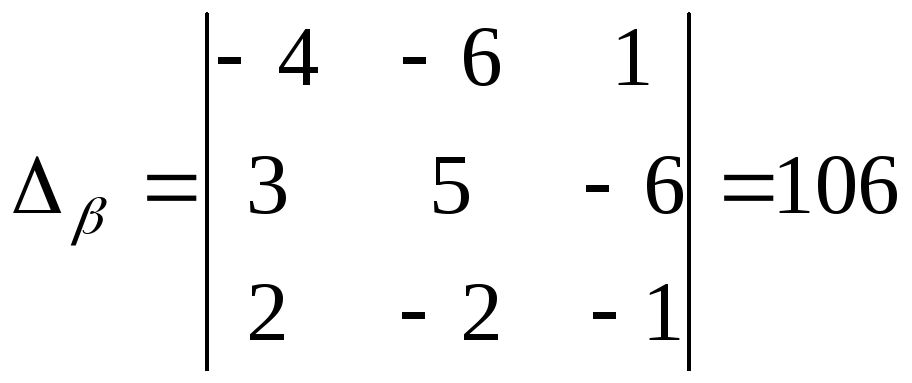 ;
;
 .
.
Имеем:
![]() ;
; ![]() ;
; ![]() .
.
Значит,
![]() .
.
Задача 2 (18)
Даны координаты вершин
пирамиды
![]() .
Найти: 1) длину ребра
.
Найти: 1) длину ребра
![]() ;
2) уравнение прямой
;
2) уравнение прямой
![]() ;
3) угол между рёбрами
;
3) угол между рёбрами
![]() и
и
![]() ;
4) уравнение плоскости
;
4) уравнение плоскости
![]() ;
5) угол между ребром
;
5) угол между ребром
![]() и гранью
и гранью
![]() ;
6) уравнение высоты, опущенной из
вершины
;
6) уравнение высоты, опущенной из
вершины
![]() на грань
на грань
![]() ;
7) площадь грани
;
7) площадь грани
![]() ;
8) объём пирамиды; 9) сделать чертёж.
;
8) объём пирамиды; 9) сделать чертёж.
![]() ;
; ![]() ;
; ![]() ;
; ![]()
Решение
1) Длина ребра
![]() численно равна расстоянию между точками
численно равна расстоянию между точками
![]() и
и
![]() ,
которое в декартовой системе координат
вычисляется по формуле
,
которое в декартовой системе координат
вычисляется по формуле
![]() ,
,
где
![]() координаты точки
координаты точки
![]() ,
,
![]() координаты точки
координаты точки
![]() .
.
Таким образом, вычисляем:
![]() .
.
2) Для составления
уравнений прямой
![]() воспользуемся формулой:
воспользуемся формулой:
![]() ,
где
,
где
![]() координаты точки
координаты точки
![]() ,
,
![]() координаты точки
координаты точки
![]() .
Тогда
.
Тогда
![]() .
.
В таком виде уравнения прямой называются каноническими. Они могут быть записаны и в виде
 или
или ![]()
т.е. уравнение прямой как линии пересечения двух плоскостей.
3) Угол
между ребрами
![]() и
и
![]() вычисляется по формуле
вычисляется по формуле
![]() из скалярного произведения векторов
из скалярного произведения векторов
![]() и
и
![]() .
.
Находим:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Поэтому
![]() ,
,
![]() .
.
4) Для составления
уравнения плоскости
![]() воспользуемся формулой
воспользуемся формулой
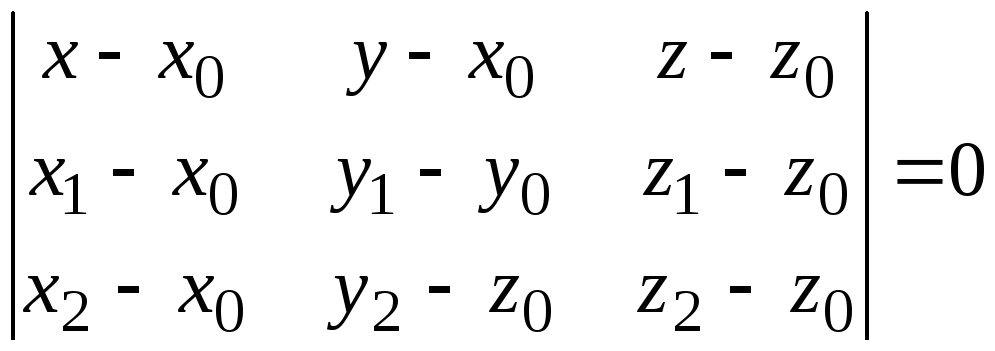 ,
где
,
где
![]() координаты точки
координаты точки
![]() ,
,
![]() координаты точки
координаты точки
![]() ,
,
![]() координаты точки
координаты точки
![]() .
.
 .
.
5) Угол
между ребром
![]() и плоскостью
и плоскостью
![]() – это угол между вектором
– это угол между вектором
![]() и его ортогональной проекцией
и его ортогональной проекцией
![]() на грань
на грань
![]() .
.
Поскольку вектор
![]() принадлежит плоскости
принадлежит плоскости
![]() ,
то угол между
ребром
,
то угол между
ребром
![]() и плоскостью
и плоскостью
![]() равен 0°
равен 0°
6) Искомое уравнение
высоты получим из канонических уравнений
прямой
![]() ,
где
,
где
![]() точка, лежащая на искомой прямой;
точка, лежащая на искомой прямой;
![]() координаты вектора
координаты вектора
![]() ,
параллельного искомой прямой. При этом
в качестве точки
,
параллельного искомой прямой. При этом
в качестве точки
![]() возьмем точку
возьмем точку
![]() ,
а в качестве вектора
,
а в качестве вектора
![]() возьмем нормальный вектор плоскости
возьмем нормальный вектор плоскости
![]() ,
т.е.
,
т.е.
![]() .
Имеем
.
Имеем
![]() .
.
7) Площадь грани
![]() находим, используя геометрический смысл
векторного произведения:
находим, используя геометрический смысл
векторного произведения:
![]()

![]()
8) Объем пирамиды
![]() численно равен одной шестой модуля
смешанного произведения векторов
численно равен одной шестой модуля
смешанного произведения векторов
![]() ,
,
![]() ,
,
![]() ,
которое находится по формуле
,
которое находится по формуле
 .
.
Таким образом,
 .
.
9) Сделаем чертёж:

Задача 3 (28)
Найти координаты точки
![]() ,
симметричной точке
,
симметричной точке
![]() относительно плоскости
относительно плоскости
![]() .
.
Решение
Составим уравнение
прямой, проходящей через точку
![]() перпендикулярно заданной плоскости:
перпендикулярно заданной плоскости:
![]() .
.
Найдём точку пересечения прямой и плоскости:

![]()
Откуда
![]() - точка пересечения прямой и плоскости.
- точка пересечения прямой и плоскости.
Точка
![]() является серединой отрезка
является серединой отрезка
![]() поэтому
поэтому

Таким образом,
![]()
Задача 4 (38)
Составить уравнение
линии, каждая точка которой равноудалена
от точки
![]() и от оси ординат.
и от оси ординат.
Решение
Обозначим произвольную
точку искомой линии как
![]() .
Тогда по условию получаем, что
.
Тогда по условию получаем, что
![]() ,
где Р – основание перпендикуляра
из точки М к прямой
,
где Р – основание перпендикуляра
из точки М к прямой
![]() .
.
Находим:
![]() ;
;
![]() .
.
Значит,
![]() .
Возводя обе части этого соотношения в
квадрат, получаем
.
Возводя обе части этого соотношения в
квадрат, получаем
![]() .
Это парабола с вершиной в точке М(4;1)
.
Это парабола с вершиной в точке М(4;1)
Полученная парабола изображена на следующем рисунке:

