Часть 1. Контрольная 2. Вариант 28

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра программного обеспечения информационных технологий

 

 

Факультет ФНиДО

Специальность ПОИТ

 

Контрольная работа № 2

по дисциплине «Высшая математика»

часть 1

Вариант № 28

 

 

 

 

 

Выполнил студент: Жукович Игорь Сергеевич

группа 291003

Студенческий билет № 2910028

Контрольная работа № 2. Основы линейной алгебры

Задача 1(48)

Доказать совместность данной системы линейных уравнений и решить её тремя методами: 1) по формулам Крамера; 2) методом Гаусса; 3) средствами матричного исчисления (с помощью обратной матрицы).

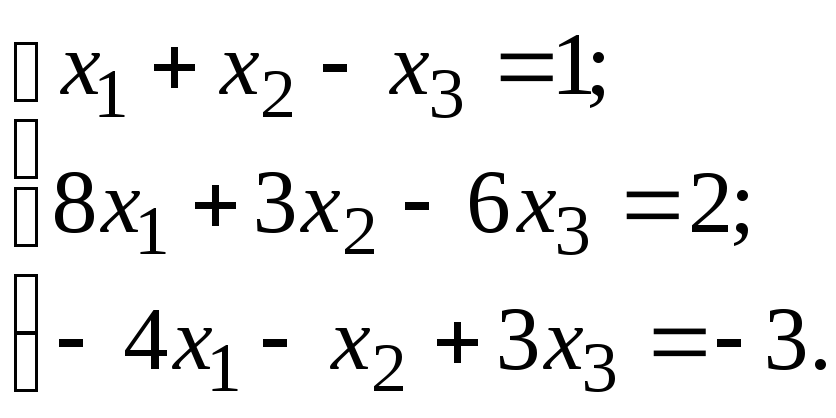
Решение

Для исследования совместности применим критерий Кронекера-Капелли. Для этого составим расширенную матрицу системы для определения её ранга и ранга матрицы коэффициентов:

.

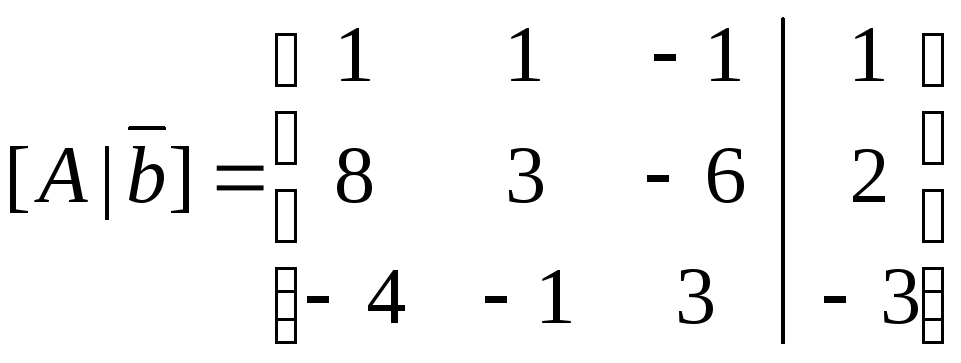Находим ранг r расширенной матрицы:

.

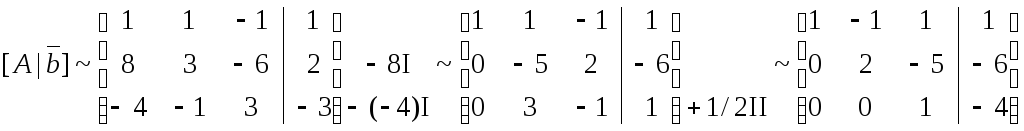Отсюда .

Следовательно, система совместна.

1) Решим систему уравнений по формулам Крамера:

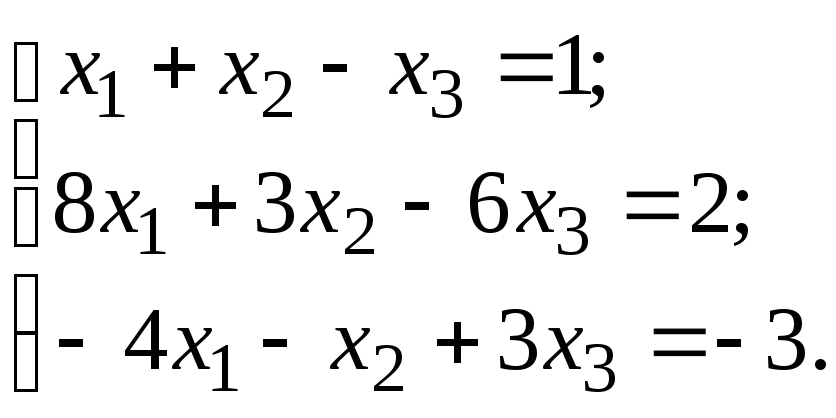
Составим матрицу коэффициентов (основную матрицу системы) и найдем её определитель:

.

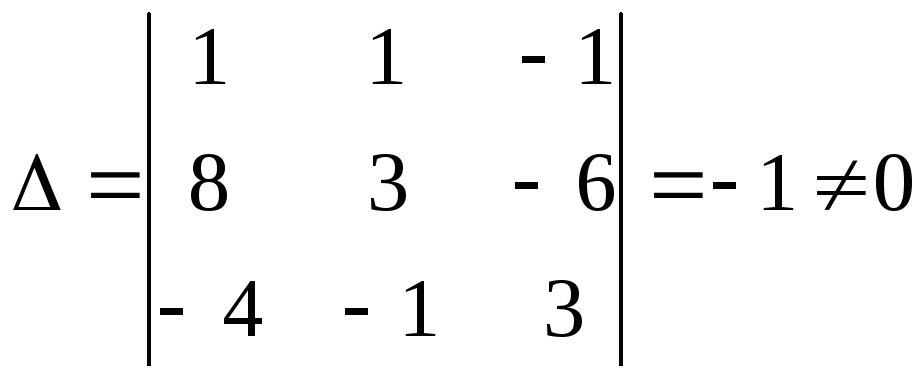Так как определитель отличен от нуля, то система совместна и имеет единственное решение. Вычисляем определители

; ; ,

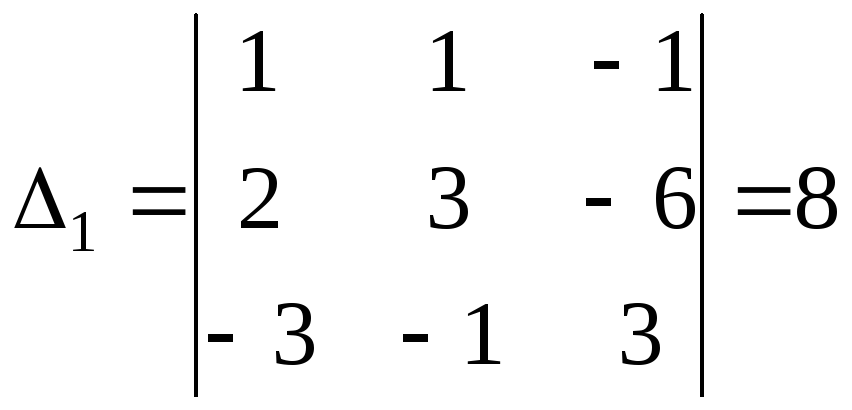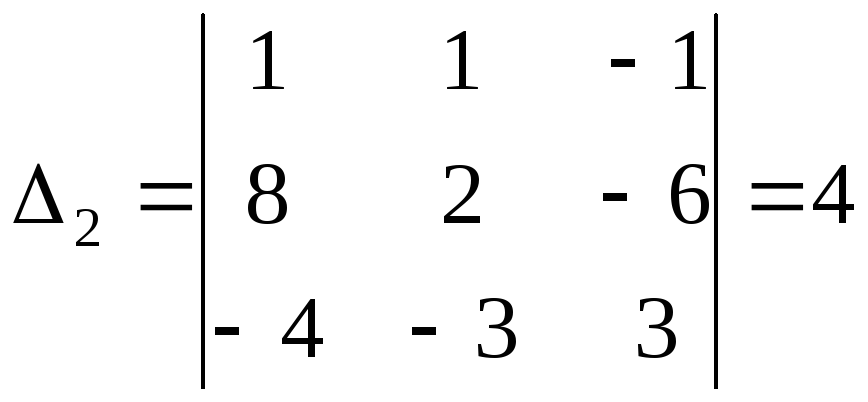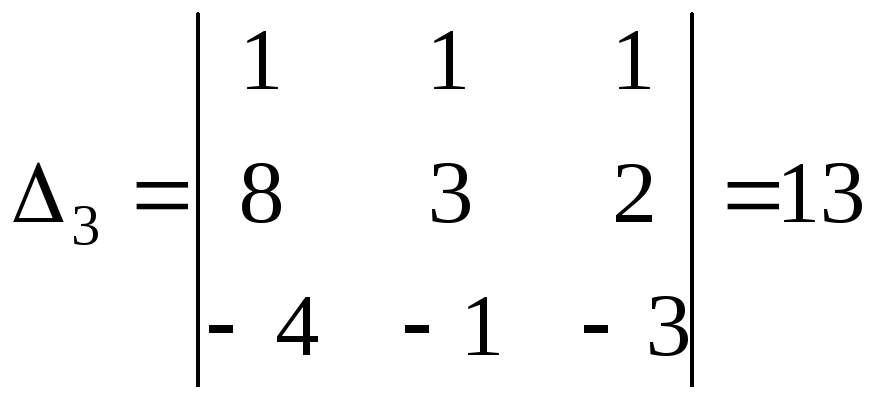которые составляем из матрицы коэффициентов путем поочередной замены каждого из столбцов на столбец правой части системы.

Далее по формулам Крамера вычисляем:

Таким образом, система имеет единственное решение , , .

2) При решении системы линейных уравнений методом Гаусса действия производятся над расширенной матрицей.

Составим расширенную матрицу системы: .

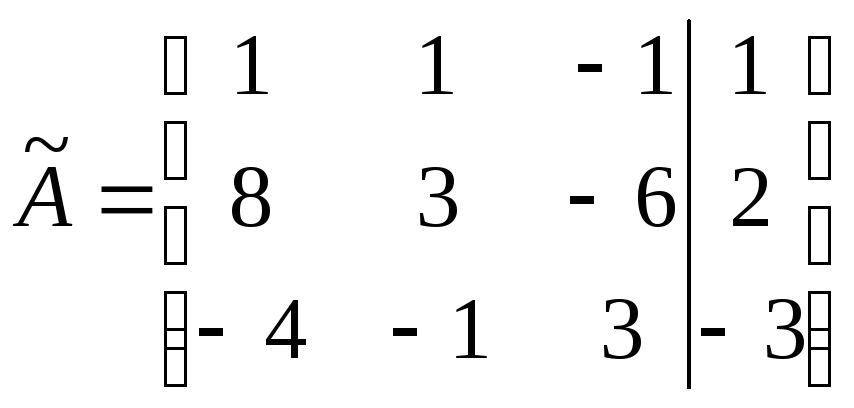Теперь приведём её путем элементарных преобразований к треугольному или трапециевидному виду. Для этого прибавим ко 2‑й строке 1‑ю, умноженную на , к 3‑й строке прибавим 1‑ю, умноженную на . Получим: .

К 3‑й строки прибавляем 2‑ю, умноженную на 3/5 получим

.

Таким образом, ранги основной и расширенной матриц равны 3. Система совместна и имеет единственное решение. Она сводится к эквивалентной системе линейных уравнений

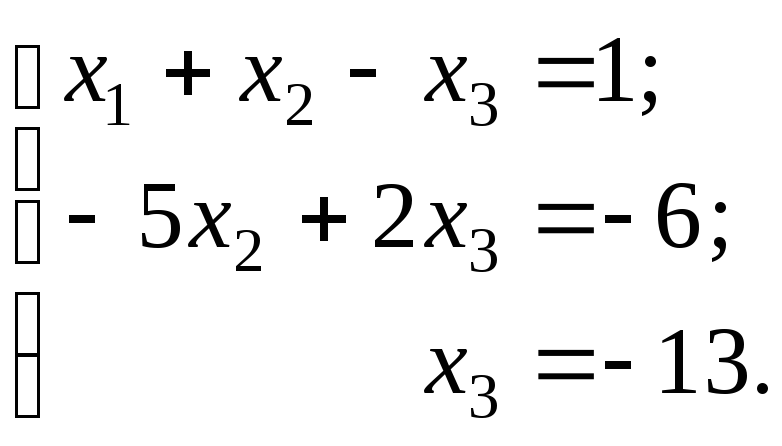
Отсюда, подставляя во второе уравнение, получим , а из первого уравнения . Итак, , , .

3) Матричный метод:

Определитель основной матрицы системы 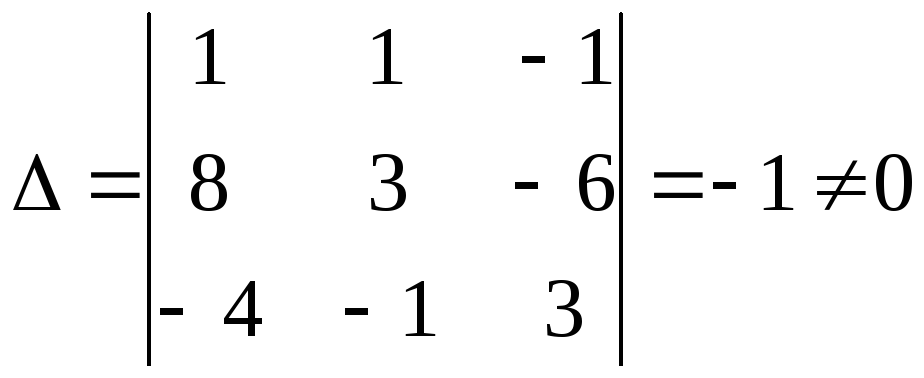, значит, система совместна и для матрицы коэффициентов существует обратная матрица. Находим решение по формуле или

,

где 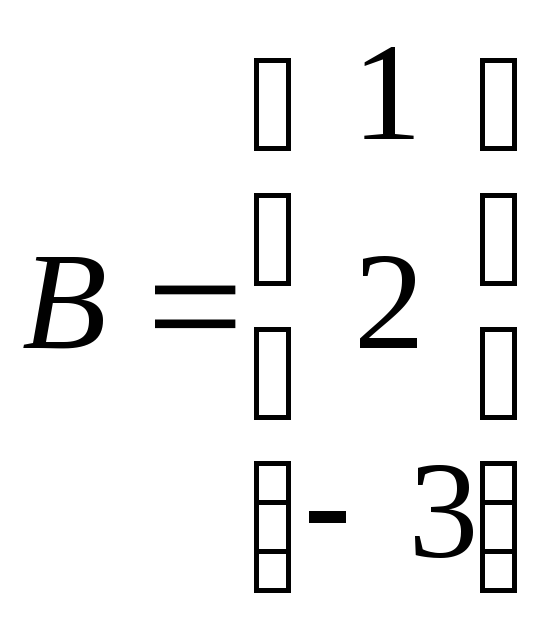, алгебраические дополнения элементов матрицы А:

Таким образом, обратная матрица к основной матрице системы имеет вид

.

Проверим правильность вычисления обратной матрицы: исходя из определения обратной матрицы, находим

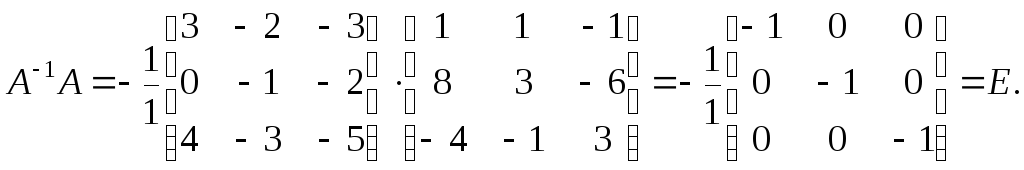
Значит, матричное решение системы имеет вид

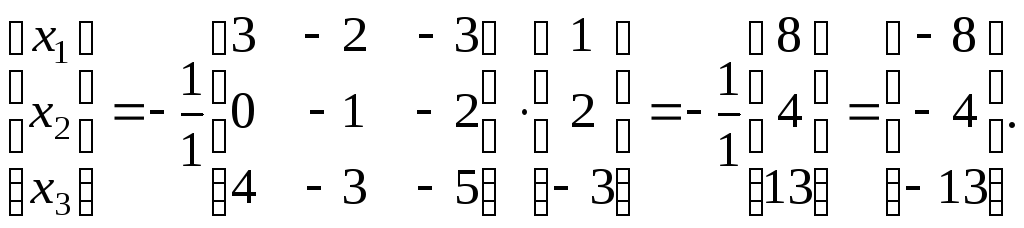
Отсюда следует, что , , .

Задача 2(58)

Найти общее решение системы линейных уравнений.

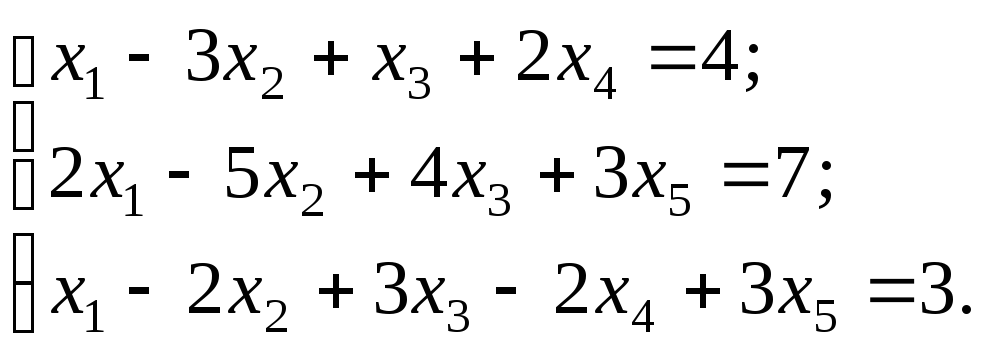
Решение

Находим ранг r расширенной матрицы:

Отсюда .

Таким образом, в данной системе линейных уравнений 2 зависимых и независимая переменные. Перенося слагаемые с х₃ , х_4, х₅ в правую часть (базисный минор образован коэффициентами при х₁, х₂, по последней матрице записываем систему

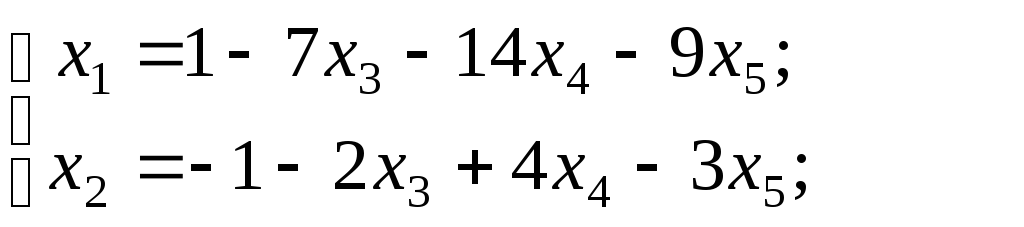
Итак, общее решение неоднородной системы линейных уравнений

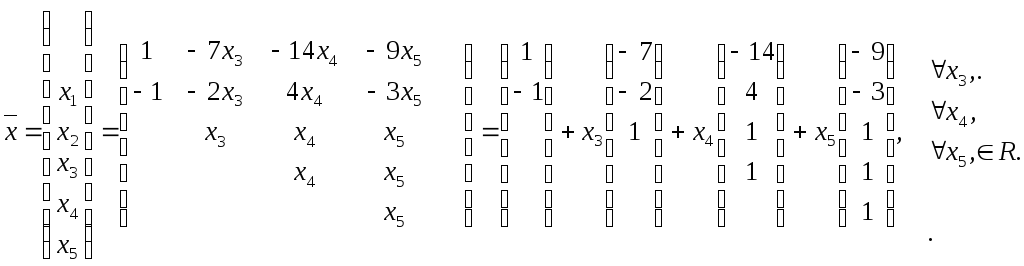
Задача 3(68)

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

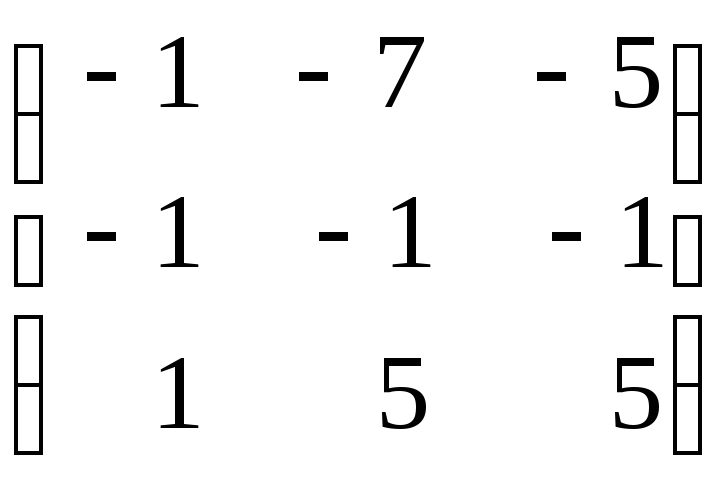
Решение

Составляем характеристическое уравнение матрицы А и находим его корни:

Так как все корни оказались действительными числами, то они являются собственными значениями матрицы А.

При система имеет вид:

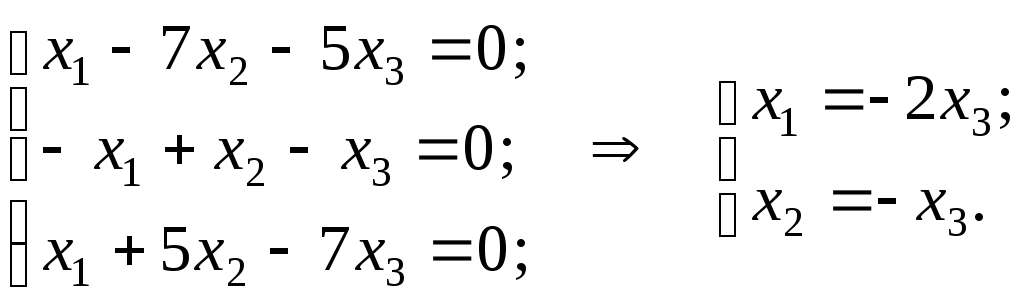
Значит, собственному значению соответствует собственный вектор

.

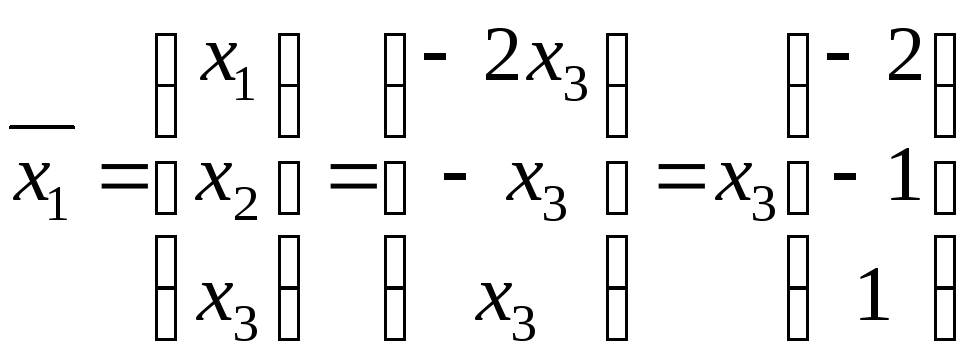Здесь х₃ – произвольное действительное число, не равное нулю. Положив его, в частности, равным единице, получим собственный вектор в виде .

Аналогично при система имеет вид:

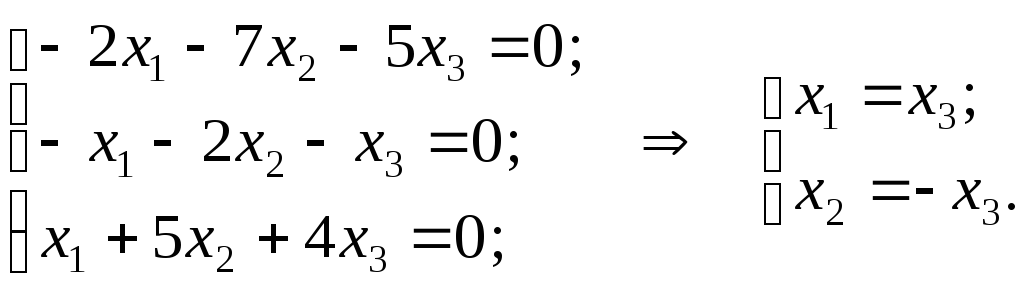
Значит, собственному значению соответствует собственный вектор

.

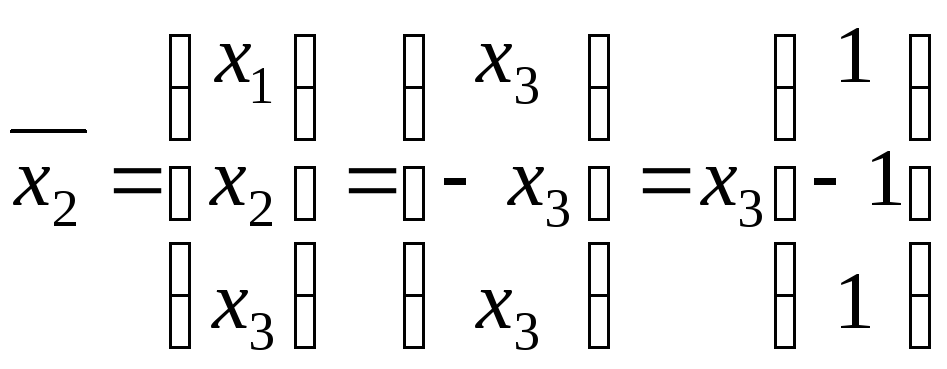Здесь х₃ – произвольное действительное число, не равное нулю. Соответствующий собственный вектор имеет вид .

Аналогично при система имеет вид:

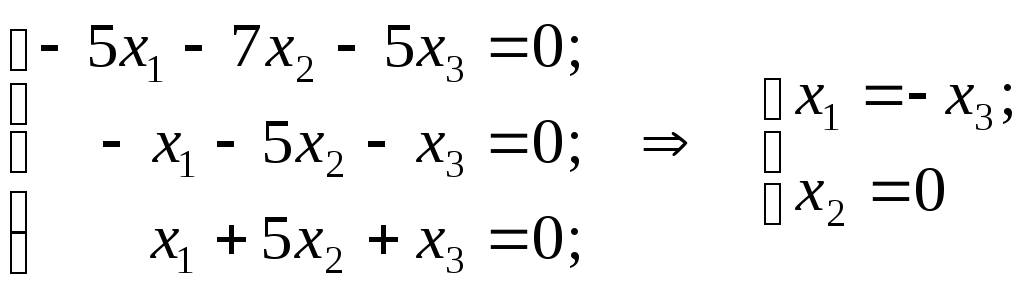
Значит, собственному значению соответствует собственный вектор

.

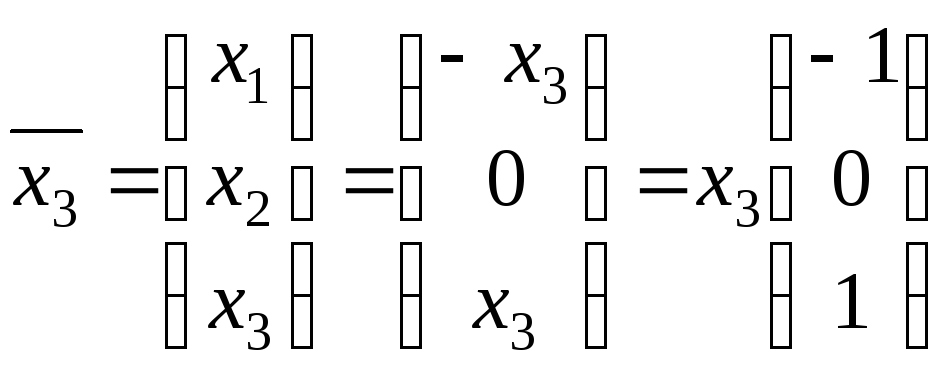Соответствующий собственный вектор имеет вид .Таким образом, матрица А имеет три собственных значения , , , а нормированные собственные векторы имеют вид

;;.

Задача 4(78)

Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка и построить её в декартовой системе координат.

Решение

Составим матрицу данной квадратичной формы и найдём её собственные значения:

.

Корнями характеристического уравнения являются числа и . Им соответствуют собственные векторы и .

Нормируя собственные векторы, получим

и .

Матрица перехода Т к новому базису имеет вид

.

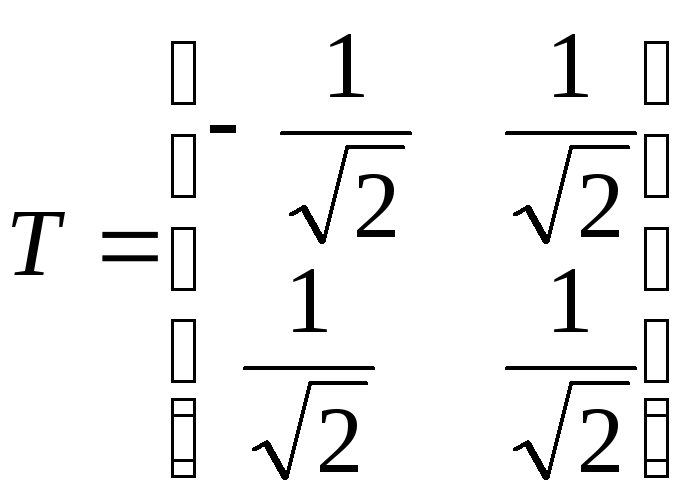Вводим замену переменных

Подставим эти выражения в исходное уравнение кривой:

.

После преобразования выражения получим

,

или . Введя замену , , получим пересекающиеся прямые