
BM часть 2. Контрольная работа №4. Вариант №8
.doc
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра программного обеспечения информационных технологий
Факультет НиДО
Специальность ПОИТ
Контрольная работа № 4
по дисциплине «Высшая математика»
Вариант № 8
Выполнил студент: ********
группа ******
Зачетная книжка № ******-**
Электронный адрес ******@****.***
Минск 2011
Задача 138
Найти производную
![]() данных
функций.
данных
функций.
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]() д)
д)
![]()
Решение:
а) Используя правило дифференцирования сложной функции:
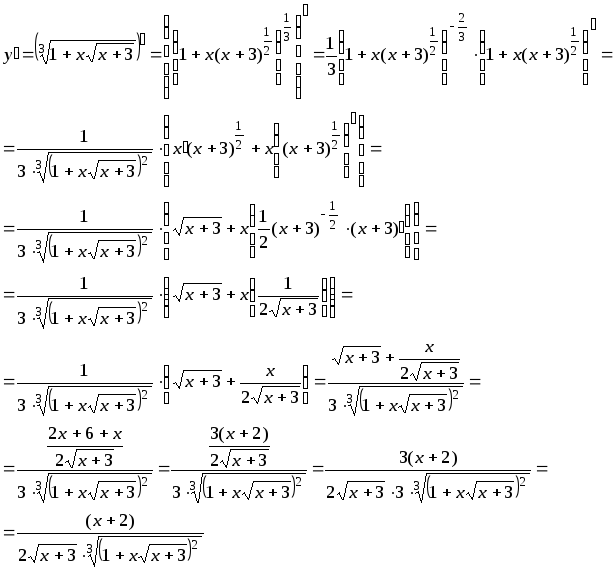 б)
Используя правило дифференцирования
сложной функции:
б)
Используя правило дифференцирования
сложной функции:
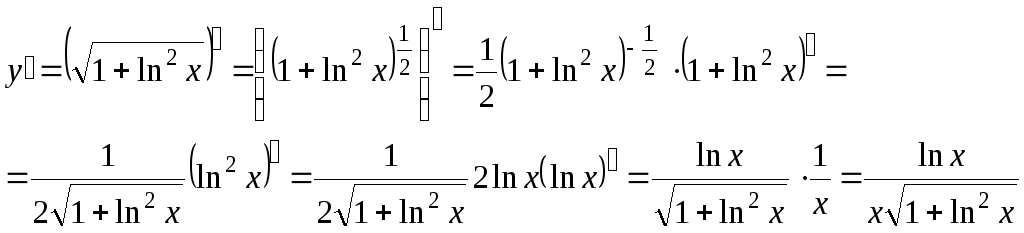
в) Используя правило дифференцирования сложной функции:
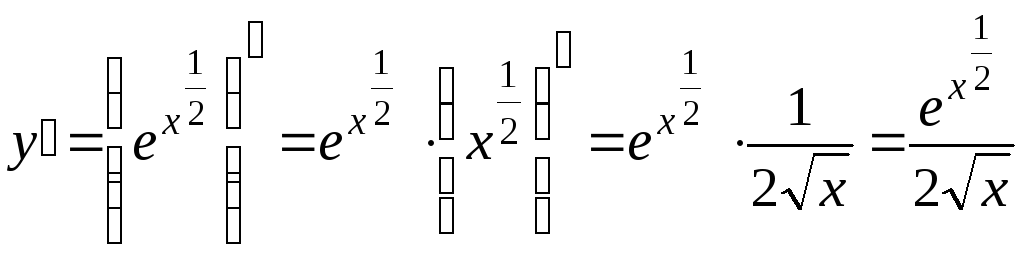
г) Используя прием логарифмического дифференцирования и правило дифференцирования сложной функции:
![]()
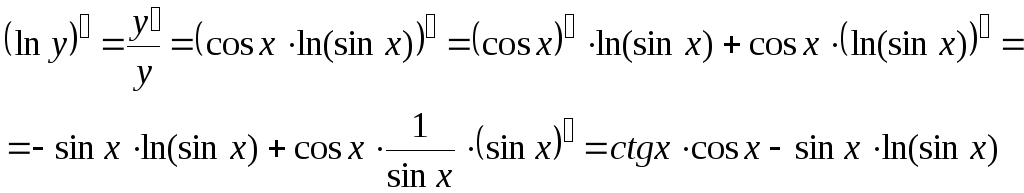
![]()
д) Продифференцируем уравнение по
![]() ,
рассматривая
,
рассматривая
![]() как функцию от
как функцию от
![]() ,
и решим полученное уравнение относительно
,
и решим полученное уравнение относительно
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
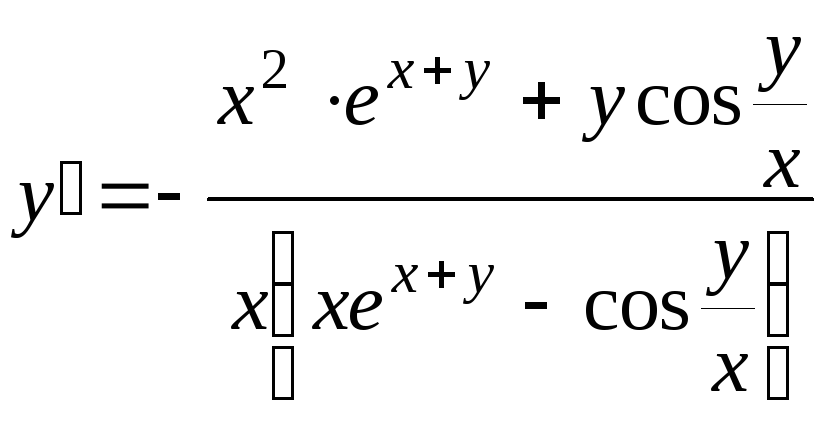
Задача 148
Найти
![]() и
и
![]()
а)![]() б)
б)
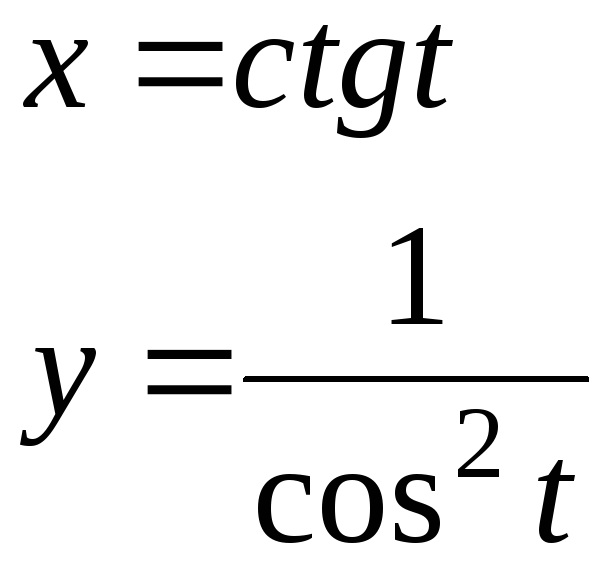
Решение:
а)
![]()

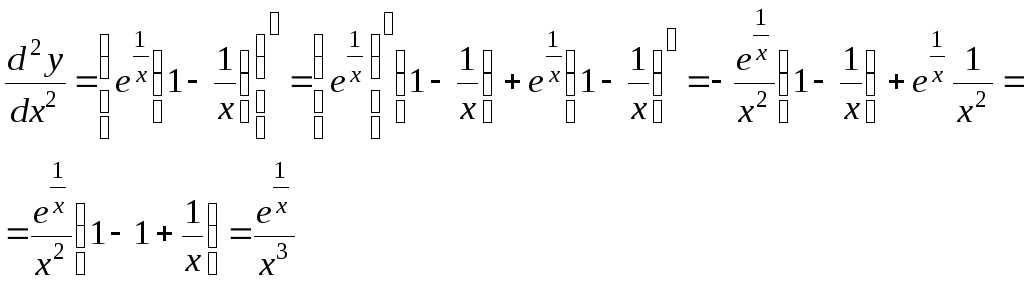
б)
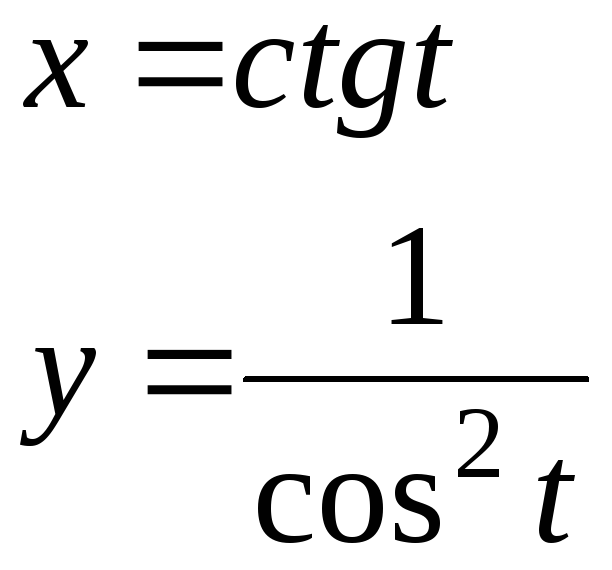
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Задача 158
Разложить функцию по формуле Тейлора
по степеням
![]() до члена
до члена
![]() .
Остаточный член записать по форме Пеано.
.
Остаточный член записать по форме Пеано.
![]() ,
, ![]()
Решение:
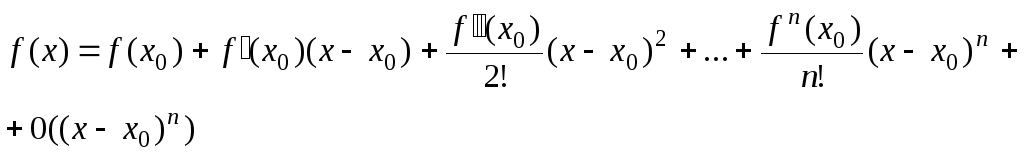
– формулой Тейлора n-го порядка с остаточным членом в форме Пеано
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Задача 168
Найти наибольшее и наименьшее значения
функции
![]() на отрезке
на отрезке
![]() .
.
![]() ,
,
![]() .
.
Решение:
Для нахождения экстремумов функции воспользуемся свойствами производных:
![]()
![]() при
при
![]() ,
где
,
где
![]()
Следовательно, на промежутке
![]() есть одна критическая точка, при
есть одна критическая точка, при
![]() .
.
Вычисляем значение функции на концах отрезка и в критической точке:
![]()
![]()
![]()
На отрезке
![]()
![]() ,
,
![]()
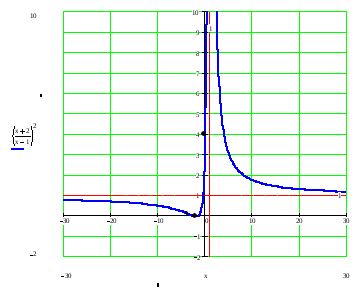
Задача 178
Исследовать методами дифференциального исчисления функции и построить ее график, используя результаты исследования.
![]()
Решение:
1) Область допустимых значений
![]()
2) Функция не является четной или нечетной,
так как
![]() и
и
![]()
3) Точки пересечения с осями координат:
![]()
![]()
![]()
![]()
![]()
![]() ,
при
,
при
![]()
![]()
![]()
4) Асимптоты:
![]() – точка разрыва, и т.к.
– точка разрыва, и т.к.
![]() ,
следовательно
,
следовательно
![]() – вертикальная асимптота графика
– вертикальная асимптота графика
Проверим, существует ли наклонная
(горизонтальная) асимптота вида
![]()
![]()
![]()
![]()
![]() – горизонтальная асимптота графика
– горизонтальная асимптота графика
5) Промежутки возрастания, убывания, точки экстремума:
Для нахождения экстремумов функции воспользуемся свойствами производных:
![]()
![]() при
при
![]()
Следовательно, на промежутке
![]() есть одна критическая точка, при
есть одна критическая точка, при
![]() .
.
На промежутке
![]()
![]() ,
следовательно функция убывает
,
следовательно функция убывает
На промежутке
![]()
![]() ,
следовательно функция возрастает
,
следовательно функция возрастает
На промежутке
![]()
![]() ,
следовательно функция убывает
,
следовательно функция убывает

![]()
Т.к.
![]() ,
то
,
то
![]() – точка минимума
– точка минимума
![]()
6) Выпуклость, вогнутость:
![]()
![]() ,
при
,
при
![]()
На промежутке
![]()
![]() ,
следовательно функция выпукла вверх
,
следовательно функция выпукла вверх
На промежутке
![]()
![]() ,
следовательно функция выпукла вниз
,
следовательно функция выпукла вниз
На промежутке
![]()
![]() ,
следовательно функция выпукла вниз
,
следовательно функция выпукла вниз
Следовательно,
![]() –
точка перегиба и
–
точка перегиба и
![]()
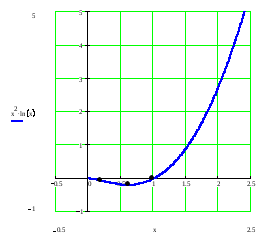
Задача 188
Исследовать методами дифференциального исчисления функции и построить ее график, используя результаты исследования.
![]()
Решение:
1) Область допустимых значений
![]()
2) Функция не является четной или нечетной,
так как
![]() и
и
![]()
3) Точки пересечения с осями координат:
![]() нет точек пересечения, т.к.
нет точек пересечения, т.к.
![]()
![]()
![]() ,
при
,
при
![]()
![]()
![]()
4) Асимптоты:
В области определения функция является непрерывной, как произведение двух непрерывных функций.
И т.к.
![]() ,
следовательно
,
следовательно
![]() не вертикальная асимптота графика
не вертикальная асимптота графика
Проверим, существует ли наклонная
(горизонтальная) асимптота вида
![]()
![]()
наклонных асимптот нет
5) Промежутки возрастания, убывания, точки экстремума:
Для нахождения экстремумов функции воспользуемся свойствами производных:
![]()
![]() при
при
![]()
Следовательно, на промежутке
![]() есть одна критическая точка, при
есть одна критическая точка, при
![]() .
.
На промежутке
![]()
![]() ,
следовательно функция убывает
,
следовательно функция убывает
На промежутке
![]()
![]() ,
следовательно функция возрастает
,
следовательно функция возрастает
![]()
![]()
Т.к.
![]() ,
то
,
то
![]() – точка минимума
– точка минимума
![]()
6) Выпуклость, вогнутость:
![]()
![]() ,
при
,
при
![]()
На промежутке
![]()
![]() ,
следовательно функция выпукла вверх
,
следовательно функция выпукла вверх
На промежутке
![]()
![]() ,
следовательно функция выпукла вниз
,
следовательно функция выпукла вниз
Следовательно,
![]() –
точка перегиба и
–
точка перегиба и
![]()
Задача 198
Найти экстремум функции с помощью производных высших порядков.
![]()
Решение:
![]()
![]() ,
где
,
где
![]() – критические точки
– критические точки
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() – точка минимума
– точка минимума
![]()
![]()
![]() – точка максимума
– точка максимума
![]()
![]()
Задача 208
Найти указанные пределы с помощью правила Лопиталя.
![]()
Решение:
![]() – правило Лопиталя
– правило Лопиталя
![]()
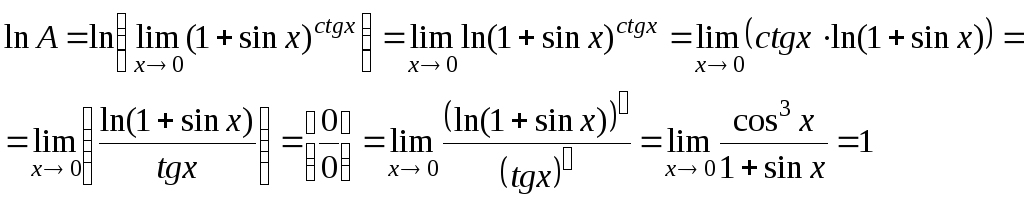
![]()
