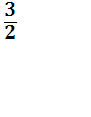вариант 10 кр №1.2
.3.docУЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет непрерывного и дистанционного обучения
Специальность: ИИ
КОНТРОЛЬНЫЕ РАБОТЫ №1,2,3
ПО ВЫСШЕЙ МАТЕМАТИКЕ
Вариант №10
Юрцевич Владислав Николаевич
Группа: 001723
Зачетная книжка:001723-10
№1-10Даны
четыре
вектора![]() (a1,a2,a3),
(a1,a2,a3),![]() (b1,b2,b3),
(b1,b2,b3),![]() (c1,c2,c3)и
(c1,c2,c3)и![]() (d1,d2,d3)
в некотором базисе.Показать что векторы
(d1,d2,d3)
в некотором базисе.Показать что векторы
![]() ,
,![]() ,
,![]() образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора ![]() в этом базисе.
в этом базисе.
Задание №10
РЕШЕНИЕ.
![]() (2,1,0),
(2,1,0),
![]() (4,3,-3),
(4,3,-3),
![]() (-6,5,7),
(-6,5,7),
![]() (34,5,-26).
(34,5,-26).
(![]() )=
)=![]() =
42+18+30
=
42+18+30![]() 28=62
28=62![]() 0
0
![]() ,
,![]() ,
,![]() – некомплонарные, т.е. они образуют
базис.
– некомплонарные, т.е. они образуют
базис.
![]() =
=![]() +
+![]() +
+![]() ,
где
,
где ![]() надо найти.
надо найти.
![]() =()
=()
![]() =()
=()
![]() =(
=(![]() )
)
![]() =(34,5,
=(34,5,![]() 26).
26).

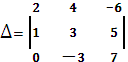 =62
=62
![]() =
=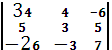 =714
=714![]() 520+90
520+90![]() 468+510
468+510![]() 140=186
140=186
![]() =
=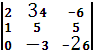 =
=![]() 156
156![]() +30+104=
+30+104=![]() 124
124
![]() =
=![]() =3
=3
![]() =
=![]() =4
=4
![]() =
=![]() =
=![]()
![]() =
=
Ответ:
![]() =
=
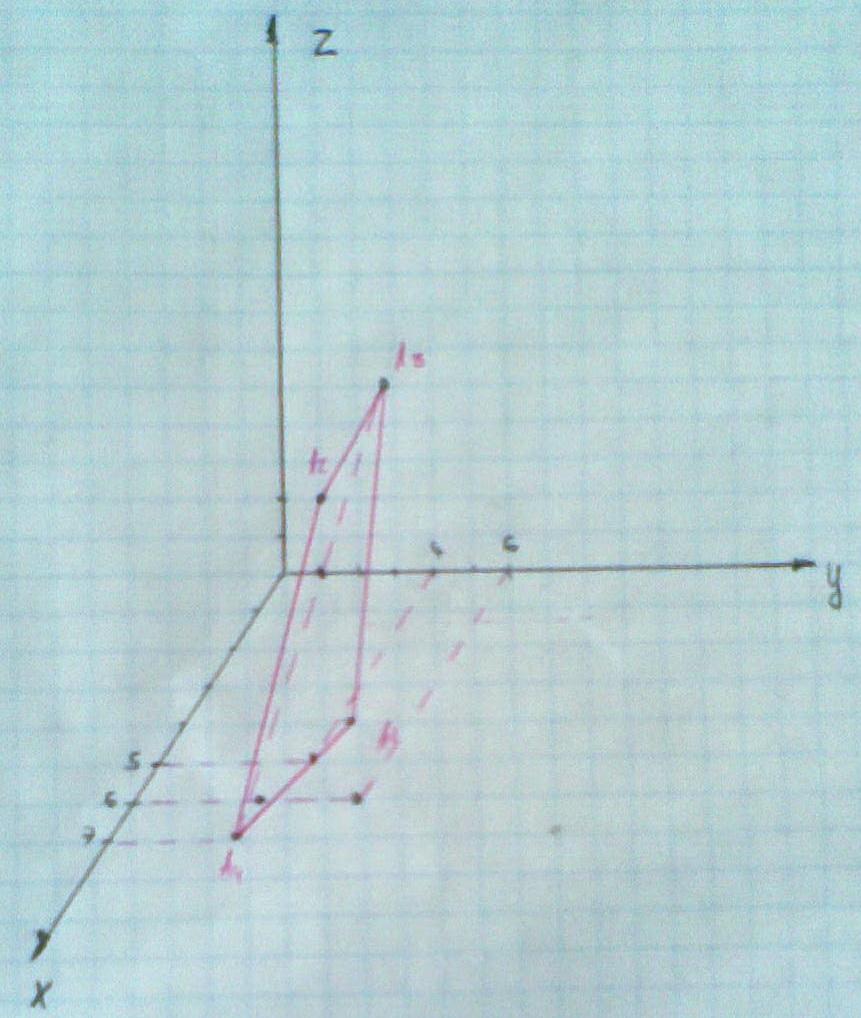
№11-20 Даны некоторые вершины пирамиды A1A2A3. Найти: 1)длину ребраA1A2; 2)угол между ребрамиA1A2 и A3A4; 3)угол между ребром A1A4 и гранию A1A2A3; 4) площадь грани A1A2A3; 5) объем пирамиды; 6) уравнения прямой A1A2; 7) уравнение плоскости A1A2A3; 8) уравнения высоты, опущенной из вершины A4 на грань A1A2A3. Сделать чертеж.
Задание №20
РЕШЕНИЕ.
![]() (6,6,2),
(6,6,2),
![]() (5,4,7),
(5,4,7),
![]() (2,4,7),
(2,4,7),
![]() (7,3,0).
(7,3,0).
1)![]() =
=![]()
2)
![]()
![]() =
=![]()
![]() =
=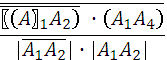 =
=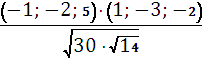 =
=![]() =
=![]() 0,244;
0,244;
![]()
3) Угол между гранью A1,A2,A3 и прямой A1,A4 находится по формуле
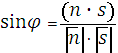
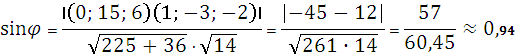
![]()
4)
![]()
![]()
![]() =
=![]()
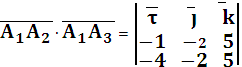 =
=![]()
![]() =
=![]()
5)
V
пир.=![]()
![]() =
=![]() =37
=37
Vпир.![]() ;
;
6)
Уравнения
прямых: ![]() и
и ![]()
![]()
![]()
![]()
![]()
![]()
![]()
И
вектор ![]() =(1;
=(1;![]() 3;
3;![]() 2)
2)![]() направл.
Вектор прямой
направл.
Вектор прямой ![]()
7)
Уравнение
плоскости ![]() .
.
![]() (
(![]() );
);
![]() (
(![]() );
);
![]() (
(![]() )
)
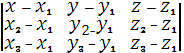 =0
=0
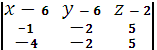 =0
=0
(![]() )
)![]() (
(![]() 6)
6)![]() +(
+(![]() 2)
2)![]() =0
=0
(![]() )-6
)-6![]() 6(
6(![]() )=0
)=0
![]() 15
15![]() 90
90![]() 6
6![]() 12=0
12=0
15y+6z![]() 102=0
102=0
![]() =(0;15;6)
=(0;15;6)
Нормальный вeктор плоскости.
8)![]() (7;3;0)
(7;3;0)
Уравнение
плоскости 15Y![]() 6Z-102=0
;
6Z-102=0
;
![]() =(0;15;6)
=(0;15;6)
Уравнение
высоты ![]() K
:
K
: ![]()
Где
– e,m,n
–координаты ![]()
Но
т.к. ![]() K
K![]() пл.
пл. ![]() , то
, то ![]() =(0;15;6)
=(0;15;6)
Уравнение высоты имеет вид
![]() =
=![]() =
=
Ответ:
1)длинна ребраA1A2=
![]() ;
2)угол между ребрамиA1A2
и A3A4=
;
2)угол между ребрамиA1A2
и A3A4=![]() ;
3)угол между ребром
A1A4
и
гранию A1A2A3=
;
3)угол между ребром
A1A4
и
гранию A1A2A3=![]() ;
4) площадь грани A1A2A3=8,1;
5) объем пирамиды=
;
4) площадь грани A1A2A3=8,1;
5) объем пирамиды=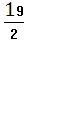 ;
6) И вектор
;
6) И вектор ![]() =(1;
=(1;![]() 3;
3;![]() 2)
2)![]() направл.
Вектор прямой
направл.
Вектор прямой ![]() ;
;
7)
![]() =(0;15;6);
8)
=(0;15;6);
8)![]() =
=![]() =
=![]()
№21-30 Дано уравнение одной из сторон квадрата x+3y-7=0 и точка пересечения его диагоналей P(0;-1). Найти уравнения трех остальных сторон этого квадрата.
Задание№30
РЕШЕНИЕ.
![]()
![]()
Пусть сторона квадрата Авимеет уравнение
![]()
![]()
Тогда
прямая AC
составляет с АВ угол 45![]()
И угловой коэф. Кас найдем из оавенства
Кав![]()

 ;
кас=
;
кас=
![]() ;
;
АС
проходит через точку ![]()
Тогда уравнение прямой АС:
![]()
![]()
Найдем т. А из решения системы
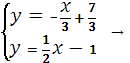
![]()
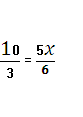 ;
.
;
. ![]()
т.А(4;1)
Найдем
координаты т. С. Т.к. ![]() середина
отрезка АС, то имеем ;
середина
отрезка АС, то имеем ;
![]()
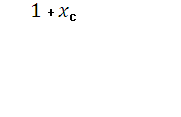
![]()
![]()
![]()
![]()
т.С.(![]() 4;
4;![]() 3)
3)
Тогда уравнение АД имеет вид
АД![]() ;
кад
;
кад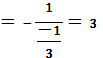
![]() ;
;
![]()
![]() ;
сл-но
;
сл-но  и проходит через т.С(-4;-3) , сл-но уравнение
ВС :
и проходит через т.С(-4;-3) , сл-но уравнение
ВС : ![]()
Сторона![]() и сл-но
и сл-но
 и СД проходит через т.С(-4;-3)
и СД проходит через т.С(-4;-3)
![]()
![]() 3;
3;
![]()
![]() СД
СД
Ответ:
ВС: ![]()
СД:
![]()
АД:
![]()
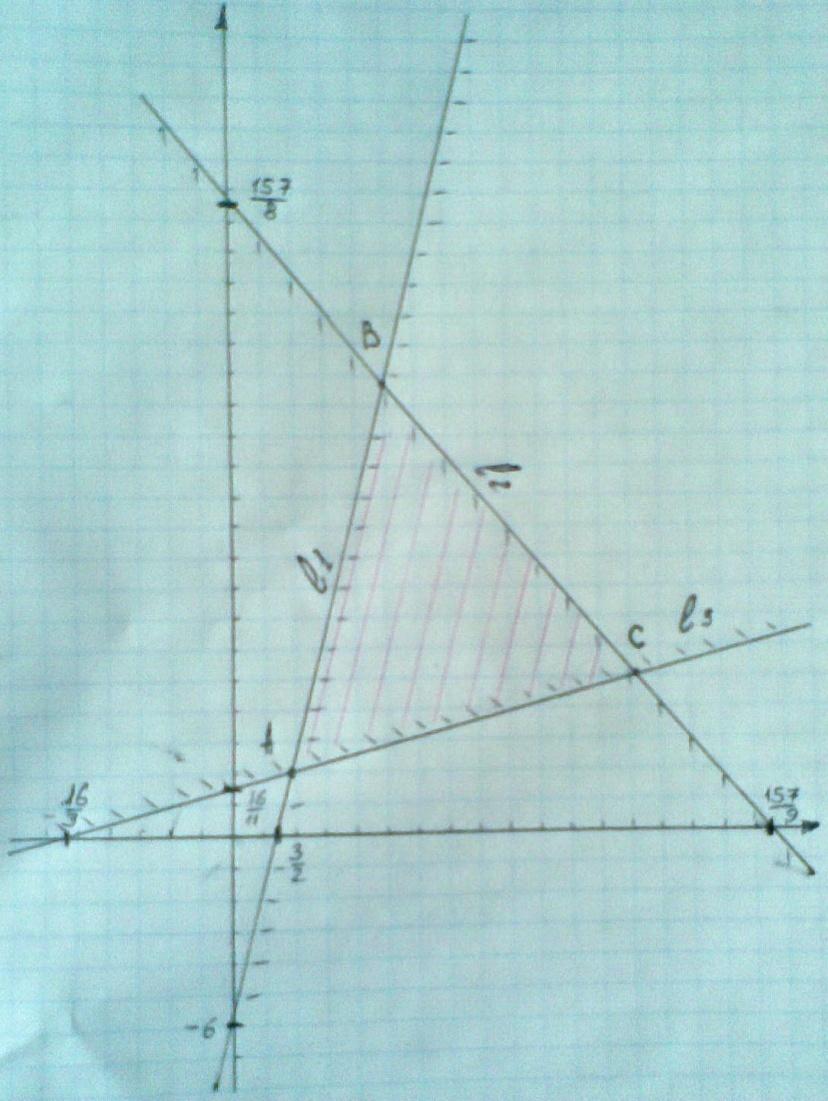
№31-40 Построить на плоскости область решений системы линейных неравенств.
Задание №40
РЕШЕНИЕ.
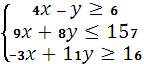
![]()
![]()
![]()
|
|
|
|
o |
-6 |
|
|
0 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
0 |
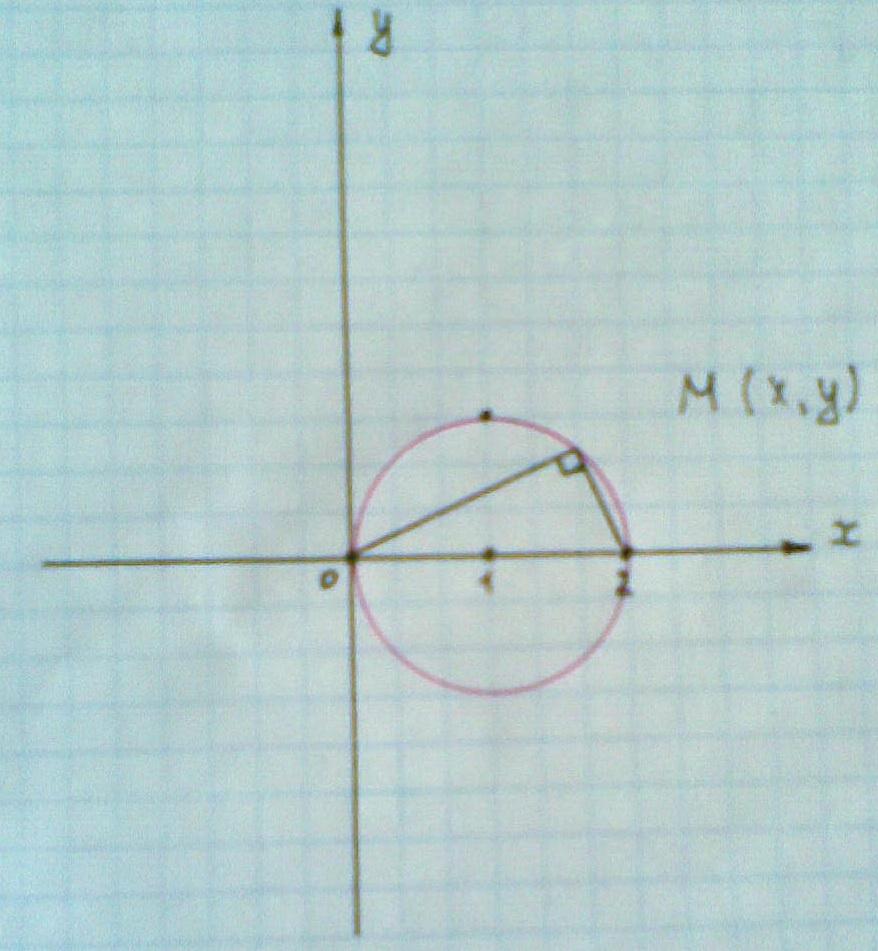
№41-50 Составить уравнение линии, каждая точка которой является основанием перпендикуляра, опущенного из начала координат на прямую, проходящую через точку А(2;0).
Задание №50
РЕШЕНИЕ.

![]()
![]()
![]()
![]()
![]()
a=1
b=0
![]() =1
=1![]()
![]()
Окружность c центром в точке (1;0)и R=1
Ответ: Окружность c центром в точке (1;0)и R=1
№51-60 Доказать совместимость данной системы линейных уравнений и решить ее двумя способами 1- Метод Гауса;2- Средствами матричного исчисления.
Задание №60
РЕШЕНИЕ.
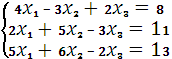
-
Метод Гауса
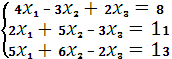
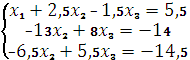
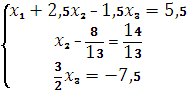
X1![]() 5
5![]() 7,5
7,5![]() 5,5
x1
5,5
x1![]() 3
3
X2
x2![]() 2
2
x3-5
x3![]() 5
5
2.Метод матричного исчисления
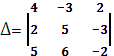 =(
=(![]() 40)+24+45-50
40)+24+45-50![]() 12+72=39≠0
12+72=39≠0
A11=(![]() 1)1+1
1)1+1![]() M11
=
M11
=![]() 10
10![]() (
(![]() 18)=8
18)=8
A12=(![]() 1)1+2
1)1+2![]() M12
=
M12
=![]() 4
4![]() (1
(1![]() 5)=11
5)=11![]() 1=
1=![]() 11
11
A13=(![]() 1)1+3
1)1+3![]() M13
=12
M13
=12![]() 25=
25=![]() 13
13![]() 1=
1=![]() 13
13
A21=(![]() 1)2+1
1)2+1![]() M21
=6
M21
=6![]() 12=
12=![]() 6
6![]()
![]() 1=6
1=6
A22=(![]() 1)2+2
1)2+2![]() M22
=
M22
=![]() 8
8![]() 10=
10=![]() 18
18![]() 1=
1=![]() 18
18
A23=(![]() 1)2+3
1)2+3![]() M23
=24
M23
=24![]() (
(![]() 15)=39
15)=39![]()
![]() 1=
1=![]() 39
39
A31=(![]() 1)3+1
1)3+1![]() M31
=9
M31
=9![]() 10=
10=![]() 1
1![]() 1=
1=![]() 1
1
A32=(![]() 1)3+2
1)3+2![]() M32
=
M32
=![]() 1
1![]() 24=
24=![]() 16
16![]()
![]() 1=16
1=16
A33=(![]() 1)3+3
1)3+3![]() M33
=20
M33
=20![]() (
(![]() 6)=26
6)=26![]() 1=26
1=26
![]() =
=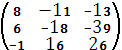 Aт=
Aт=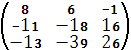
A-1=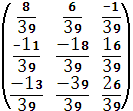 A=
A= ![]() A
A![]() A-1=E
A-1=E
Проверка
A![]() A-1=
A-1=![]() =E
=E
A-1![]() B=X
B=X
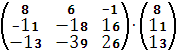 =
=![]()
X=![]() X1=3
X2=
X1=3
X2=![]() 2
X3=
2
X3=![]() 5
5
Ответ
: X1=3
X2=![]() 2
X3=
2
X3=![]() 5
5
№61-70 Найти размерность и базис пространства решений однородной системы линейных уравнений.
Задание №70
РЕШЕНИЕ.
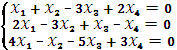
![]() ra=2
ra=2
Пологаем
![]() =
=![]()