Контрольная работа №10 (4 часть) 5 вариант
.doc№1
485. Представить заданную функцию w=f (z), где z = x + iy, в виде w = u(x,y) + iv(x,y); проверить, является ли она аналитической. Если да, то найти значение ее производной в заданной точке z0. ω=e1−2iz , z0 = π/6
Решение
ω=e1−2iz =e1−2i(x+iy) =e1+2y−2ix =e1+2y(cos2x−isin2x) то есть u=e1+2ycos2x; v=e1+2ysin2x
Проверим условие Коши-Римана, для этого найдем частные производные.
Таким образом, 
и 
и функция дифференцируема.
Найдем производную ω′ = −2e1−2iz. Тогда ω′( π/6) = −2e1−iπ/3.
№2
495. Найти все лорановские разложения данной функции по степеням z - z0
Решение
Функция имеет две особые точки z1 = −3;z2 = 1.
Следовательно, имеются три области с центром в точке z0 = −2 + 2i.
Вычислим |z0
− (−3)| = |1 + 2i| = 
,
|z0
− 1| = |−3+2i|= 
.
Используя метод неопределенных коэффициентов разложим дробь на простейшие, получим
Рассмотри три области
I. Круг
Ряд сходится при 
II. Кольцо
сходится при 
Второе слагаемое представим в виде
Ряд сходится при 
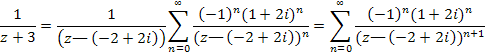
Окончательно 
III.
сходится при 
представим в виде
Ряд сходится при 
Окончательно 
№3
505. Определить область (круг) сходимости данного ряда и исследовать сходимость его (расходится, сходится условно, сходится абсолютно) в точках z1, z2 , z3 .
Решение
Применим признак Коши:
Ряд сходится в кольце
1. При 
получим ряд
Этот ряд сходится по признаку Коши
2. При 
получим ряд
Этот ряд сходится условно по признаку Лейбница
3. При 
получим ряд
Т.к. 
то ряд расходится
№4
515.При помощи вычетов вычислить данный интеграл по контуру l.
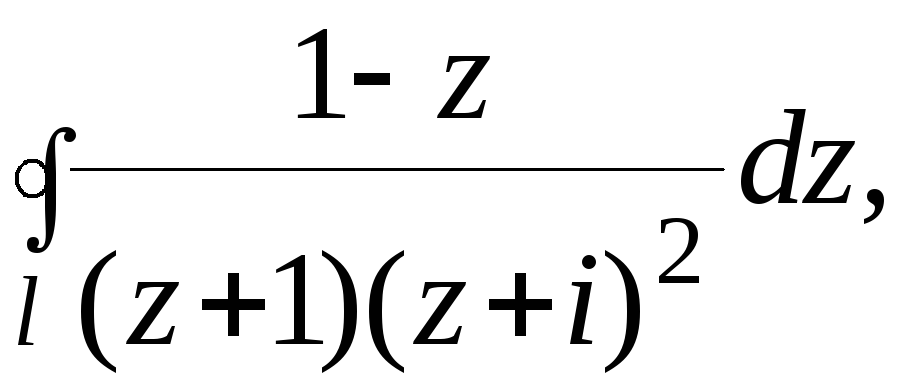
Решение
– окружность, полюсы 
находятся внутри замкнутого круга.
Найдем вычеты:
Тогда
