Элементы векторной алгебр и аналитической геометрии

Задачи 1-10. Даны векторы a,b,c,d. Для указанных в пп. 1-3 векторов требуется: 1) вычислить скалярное произведение векторов из пункта; 2) найти модуль векторного произведения векторов; 3) проверить коллинеарность и ортогональность векторов; 4) убедиться, что векторы a,b,c образуют базис; 5) найти координаты вектора d в этом базисе.

1., , ,;

1) 3a, 2c; 2) b, -4c; 3) a, c.

1) вычислить скалярное произведение векторов из пункта

Ответ: - 48

2)

Обозначим векторное произведение векторов и через m

, 0<φ<180

ответ:

3) проверить коллинеарность и ортогональность векторов

Необходимое и достаточное условие коллинеарности двух векторов:

В координатной форме должны выполняться равенства

так как , то данные вектора не являются коллинеарными.

Условие ортогональности векторов

Следовательно, вектора a и c не являются ортогональными.

4) убедиться, что векторы a,b,c образуют базис

,

Векторы , и образуют базис, если они линейно независимы

Матрица системы векторов имеет вид:

Вычислим определитель этой матрицы:

Значит, ранг матрицы равен 3 и вектора линейно независимы и образуют базис.

5) найти координаты вектора d в этом базисе.

найдем разложение вектора по базису

Вектор представляется единственным образом в виде

В координатной форме имеем систему трех уравнений с тремя неизвестными:

Решим систему по правилу Крамера.

; ;

Ответ:

Задачи 11-20. Даны вершины A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) треугольника ABC. Требуется найти:

1) уравнение стороны AB;

2) уравнение высоты CH и длину этой высоты;

3) уравнение медианы AM;

4) точку N пересечения медианы AM и CH;

5) уравнение прямой, параллельной стороне AB и проходящей через вершину C;

6) внутренний угол при вершине A и внешний угол при вершине C.

11. A(-2,4), B(3,1), C(10,7).

1) уравнение стороны AB

Уравнение прямой на плоскости, проходящей через две точки, имеет вид:

Ответ: 3y+5y – 14 = 0

2) уравнение высоты CH и длину этой высоты;

прямая СH перпендикулярна АВ

Условие перпендикулярности прямых: , где – их угловые коэффициенты.

Найдем угловой коэффициент прямой АВ:

,

- угловой коэффициент прямой СН.

Составим уравнение прямой СН по точке С(10;7) и угловому коэффициенту

- уравнение прямой СН.

Найдем координаты точки пересечения прямых АВ и СН

H (

Найдем длину высоты СН:

Ответ:

3) уравнение медианы АМ

М – середина отрезка ВС, В(3;1), С(10;7)

Координаты середины отрезка находим по формулам:

,

M=(

Составим уравнение прямой АМ по двум точкам:

, ,

- уравнение медианы АМ Ответ: y=4

4) точку N пересечения медианы AM и CH;

координаты точки N пересечение медианы АМ и высоты СН находим, решая систему уравнений:

N=(8,2;4)

Ответ: N (8,2;4)

5) уравнение прямой, параллельной стороне AB и проходящей через вершину C;

условие параллельности прямых:

Угловой коэффициент прямой АВ равен ( из пункта 2) значит, угловой коэффициент искомой прямой по точке

Составим уравнение прямой по точке С(10;7) и угловому коэффициенту :

- уравнение прямой параллельной АВ и проходящей через точку С

Ответ:

6) внутренний угол при вершине A и внешний угол при вершине C.

Внешний угол при вершине С – это угол между векторами и

Ответ: ;

Задачи 21-30. Составить канонические уравнения 1) эллипса, 2) гиперболы, 3) параболы по известным из условий 1 – 3 параметрам. Через a и b обозначены большая и малая полуоси эллипса или гиперболы, через F – фокус кривой, – эксцентриситет, 2 c – фокусное расстояние, – уравнения асимптот гиперболы, D – директриса кривой, A, B– точки, лежащие на кривой.

21.

1) Эллипс b=15 – малая полуось эллипса, F(-10;0) – фокус эллипса

Отсюда имеем b=15 c=10

Уравнение эллипса имеет вид:

Ответ:

2) гипербола

a - большая полуось гиперболы

- эксцентриситет гиперболы

Имеем: a=13

Уравнение гиперболы имеет вид:

Ответ:

3) Парабола D : x= - 4

D- директриса кривой

Ответ:

Задачи 31-40. Даны четыре точки A₁(x₁,y₁,z₁), A₂(x₂,y₂,z₂), A₃(x₃,y₃,z₃), A₄(x₄,y₄,z₄). Требуется найти:

1) уравнение плоскости A₁A₂A₃;

2) уравнение прямой, проходящей через точку A₄, перпендикулярно плоскости A₁A₂A₃;

3) расстояние от точки A₄ до плоскости A₁A₂A₃;

4) синус угла между прямой A₁A₄ и плоскостью A₁A₂A₃;

5) косинус угла между координатной плоскостью Oxy и плоскостью A₁A₂A_3.

31. A₁(3,-1,2), A₂(-1,0,1), A₃(1,7,3), A₄(8,5,8).

1) найти уравнение плоскости A₁A₂A₃;

уравнение плоскости, проходящей через три заданные точки, имеют вид:

Ответ:

2) уравнение прямой, проходящей через точку A₄, перпендикулярно плоскости A₁A₂A₃;

A₄(8,5,8)

Уравнение плоскости A₁A₂A₃ имеет вид:

- вектор перпендикулярный плоскости, следовательно, это направляющий вектор искомой прямой.

Уравнение прямой имеет вид:

где ()- координаты точки на прямой,

(m,n,p)-координаты направляющего вектора.

Ответ:

3) расстояние от точки A₄ до плоскости A₁A₂A₃

A₄(8;5;8) Уравнение плоскости A₁A₂A₃:

Расстояние от точки до плоскости находится по формуле:

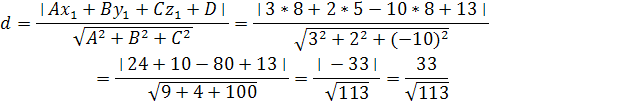
Ответ:

4) синус угла между прямой A₁A₄ и плоскостью A₁A₂A₃

Составим уравнение прямой A₁A_4: : А₁(3;-1;2),А₄(8;5;8) по формулам:

Уравнение плоскости A₁A₂A₃:

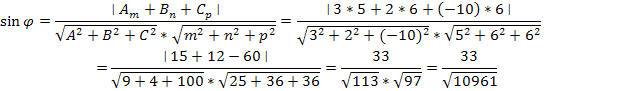
Ответ:

5) косинус угла между координатной плоскостью Oxy и плоскостью A₁A₂A_3.

Уравнение плоскости Oxy : z=0

Уравнение плоскости A₁A₂A₃ :

Ответ: