
- •1. Элементы линейной алгебры и аналитической геометрии
- •1. Даны векторы a(a1; a2; a3), b(b1; b2; b3), c(c1; c2; c3) и d(d1; d2; d3) в некотором базисе. Показать, что векторы a, b, c образуют базис, и найти координаты вектора d в этом базисе.
- •16. Даны координаты вершины пирамиды а1а2а3а4 .Найти:
- •26. Составить уравнение линии, для каждой точки расстояния от начала координат и от точки а(0,5) относятся, как 3:2.
- •36. Доказать совместность данной системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.
- •46. Найти размерность и базис пространства решений однородной системы линейных уравнений
- •56. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матриц.
- •66. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм
- •2. Введение в анализ
- •96. Найти пределы функций, не пользуясь правилом Лопиталя:
26. Составить уравнение линии, для каждой точки расстояния от начала координат и от точки а(0,5) относятся, как 3:2.
Пусть M(x;y) – произвольная точка искомой кривой. Найдем нужные расстояния:
d
=
![]() =
=
![]() – расстояние от начала
координат до
произвольной точки кривой;
– расстояние от начала
координат до
произвольной точки кривой;
d
=
![]() =
=
![]() – расстояние от точки А до произвольной
точки кривой. Тогда
– расстояние от точки А до произвольной
точки кривой. Тогда
![]() или
или ![]() ;
;

Это окружность с центром в точке (0;9) и радиусом равным 6.
36. Доказать совместность данной системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.

1) Для решения системы методом Гаусса рассмотрим расширенную матрицу системы и приведем ее к треугольному виду:
 = [умножаем первую
строку на -4, вторую на 7 и складываем их,
умножаем первую на -2, третью на 7 и
складываем их ] =
= [умножаем первую
строку на -4, вторую на 7 и складываем их,
умножаем первую на -2, третью на 7 и
складываем их ] =
 = [умножаем третью строку на 97, вторую
на -31 и складываем их] =
= [умножаем третью строку на 97, вторую
на -31 и складываем их] =
Ранг расширенной матрицы равен числу ненулевых строк, т.е. равен 3. Теперь рассмотрим матрицу А и приведём её к треугольному виду аналогичными действиями:
 .
.
Ранг матрицы равен числу ненулевых строк, т.е. равен 3. Так как ранг матрицы системы совпадает с рангом расширенной матрицы, то система совместна.
Тогда получим систему:

Тогда получим решение:
x3 = -3; x2 = -4; x1 =2.
2) Для решения
матричным методом нужно рассмотреть
матричное уравнение: AX
= B,
где A
=
 ,
X
=
,
X
=
![]() ,
B
=
,
B
=
 .
.
Тогда X = A-1B.
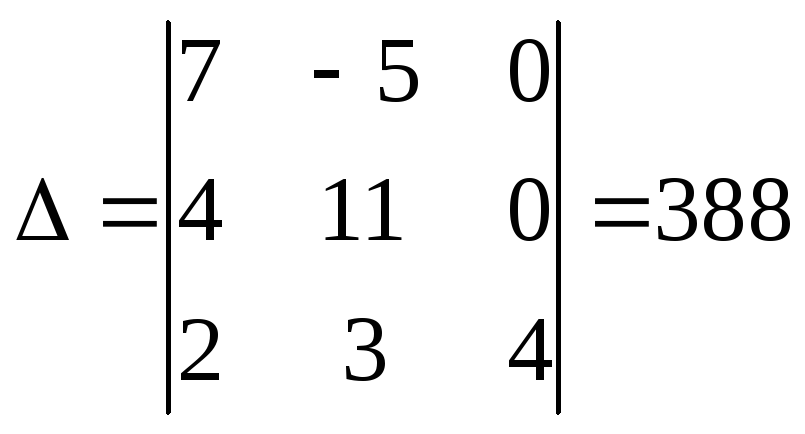
Вычислим обратную
матрицу
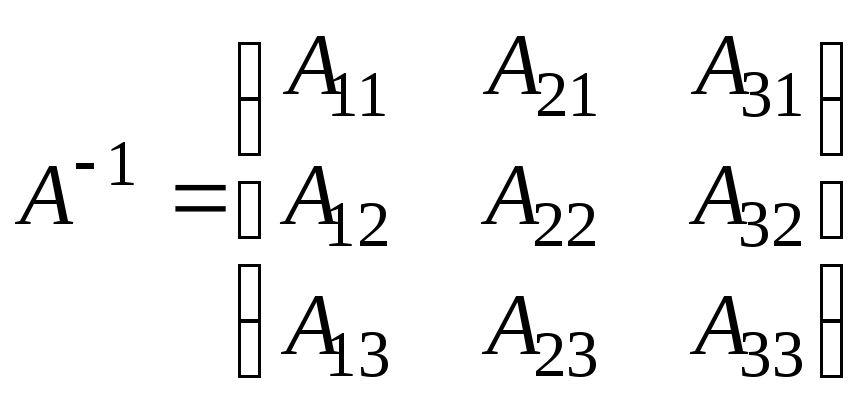 .
.



Тогда A-1
=

Получим X
= A-1B
=
 =
=
 =
=
![]() .
.
46. Найти размерность и базис пространства решений однородной системы линейных уравнений

Рассмотрим расширенную матрицу системы и приведем ее к треугольному виду:
 = [умножаем первую
строчку на -2 складываем со второй,
умножаем первую на -1 и складываем с
третьей] =
= [умножаем первую
строчку на -2 складываем со второй,
умножаем первую на -1 и складываем с
третьей] =
 =
=
[складываем вторую
строку с третьей] =
 .
.
Ранг расширенной матрицы равен числу ненулевых строк, т.е. равен 3. Теперь рассмотрим матрицу А и приведём её к треугольному виду аналогичными действиями:
 .
.
Ранг матрицы равен числу ненулевых строк, т.е. равен 3. Так как ранг матрицы системы совпадает с рангом расширенной матрицы, то система совместна.
Тогда получим систему:
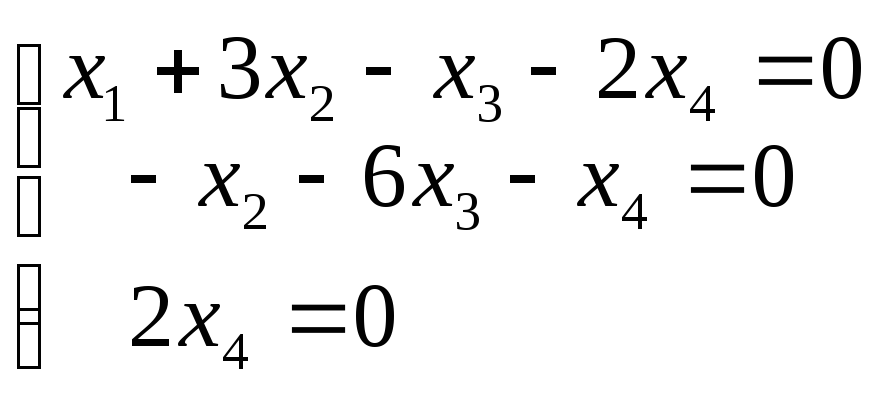
Пусть х3=t, тогда получим решение:
х4=0,
x3
= t;
x2
=![]() ;x1
=
;x1
=
![]() ,
где t – любое число.
,
где t – любое число.
56. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матриц.

Характеристическое уравнение имеет вид:
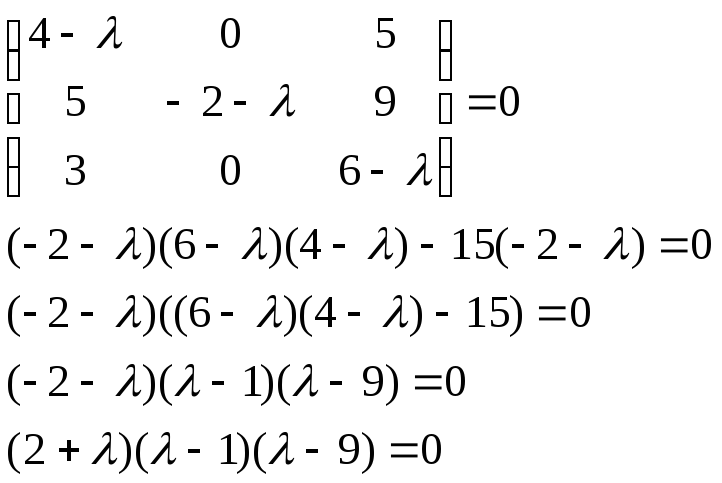
![]() 1=-2,
1=-2,
![]() 2=1,
2=1,
![]() 3=9
– собственные значения линейного
преобразования.
3=9
– собственные значения линейного
преобразования.
Для
![]() 1=-2
найдём собственный вектор.
1=-2
найдём собственный вектор.

Собственный вектор
для
![]() 1=-2
имеет вид (0;m;0).
1=-2
имеет вид (0;m;0).
Для
![]() 2=1
найдём собственный вектор.
2=1
найдём собственный вектор.

Собственный вектор
для
![]() 2=1
имеет вид (
2=1
имеет вид (![]() ;
;![]() ;t).
;t).
Для
![]() 3=9
найдём собственный вектор.
3=9
найдём собственный вектор.
 .
.
Собственный вектор
для
![]() 3=9
имеет вид (s;
3=9
имеет вид (s;![]() ;s).
;s).
66. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм
![]()
Запишем данное
уравнение в виде:
![]()
Найдём матрицу Т
ортогонального оператора, приводящего
данную квадратичную форму ![]() к каноническому
виду.
к каноническому
виду.
Запишем характеристическую матрицу:

Её корнями являются
значения
![]() 1=1,
1=1,
![]() 2=10.
2=10.
Для
![]() 1=1
найдём собственный вектор.
1=1
найдём собственный вектор.
 ,
где t
– любое число.
,
где t
– любое число.
Собственный
вектор-столбец для
![]() 1=1
имеет вид
1=1
имеет вид
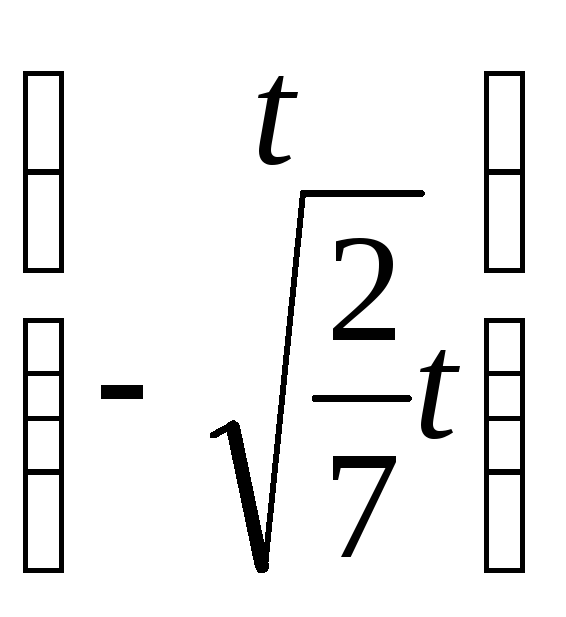 .
Тогда
.
Тогда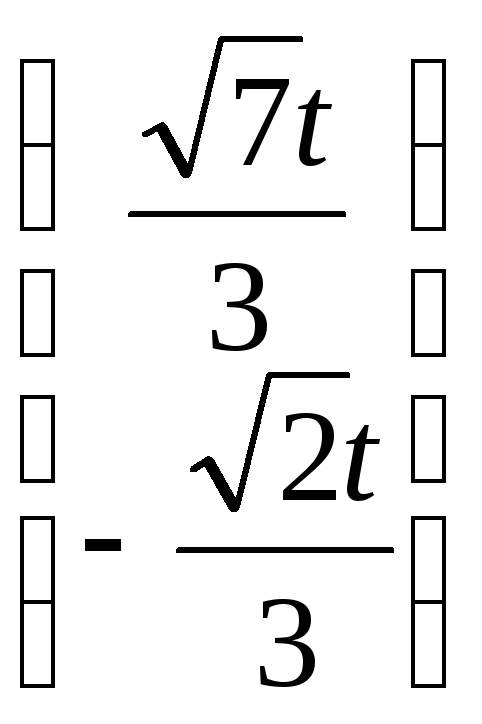 есть нормированный собственный
вектор-столбец.
есть нормированный собственный
вектор-столбец.
Для
![]() 2=10
найдём собственный вектор.
2=10
найдём собственный вектор.
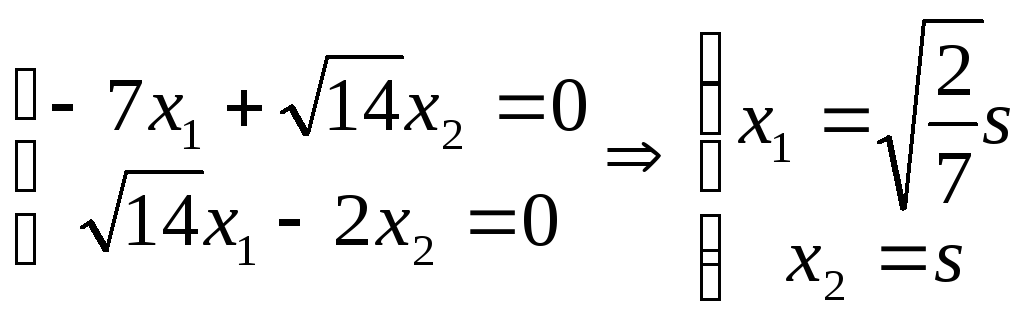 ,
где s
– любое число.
,
где s
– любое число.
Собственный
вектор-столбец для
![]() 2=10
имеет вид
2=10
имеет вид
 .
Тогда
.
Тогда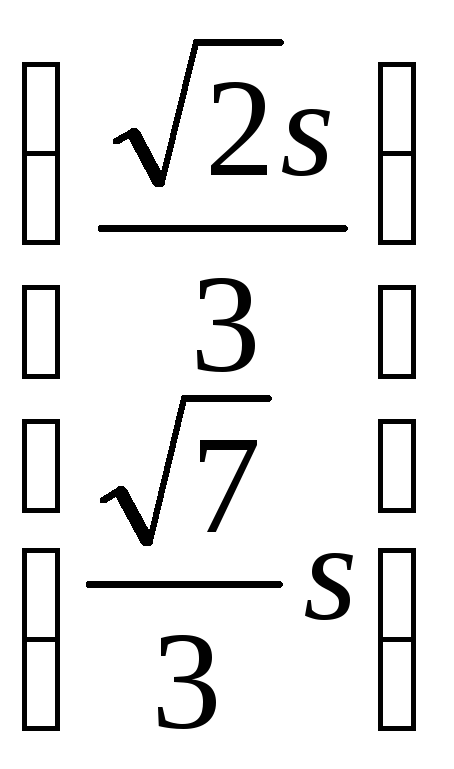 есть нормированный собственный
вектор-столбец.
есть нормированный собственный
вектор-столбец.
Ортогональный
оператор, приводящий квадратичную форму
к каноническому виду, имеет матрицу
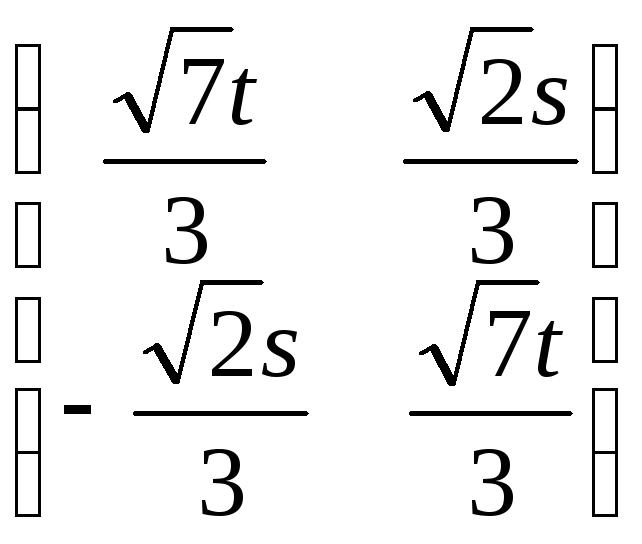 .
.
Базисными векторами
новой системы координат
![]() являются:
являются:
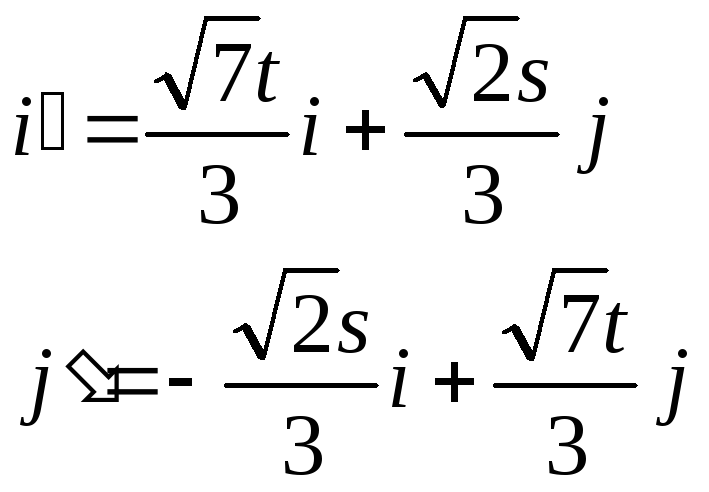
В системе координат
![]() уравнение данной фигуры примет вид:
уравнение данной фигуры примет вид:

Это эллипс, центр
которого находится в точке (0,0) относительно
системы координат
![]() ,
а оси симметрии параллельны координатным
осям этой системы.
,
а оси симметрии параллельны координатным
осям этой системы.
