Высшая математика Контрольная №3 Вариант №3

№83

Выделив в заданной функции полный квадрат, получить уравнение параболы и построить ее график.

Решение:

- парабола с вершиной в точке (-2;-3).

- сдвиг влево на 2 ед. параболы

- растяжение в 2 раза вдоль оси Oy параболы

- сдвиг вниз на 3 ед. гр. Функции

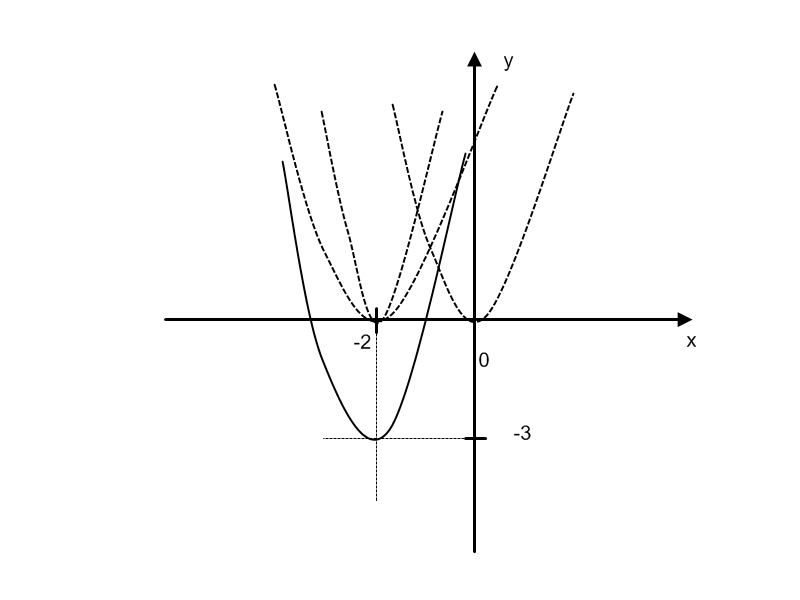
№93

Дана функция на отрезке Требуется:

1. Построить график функции в полярной системе координат по точкам, давая значения через промежуток

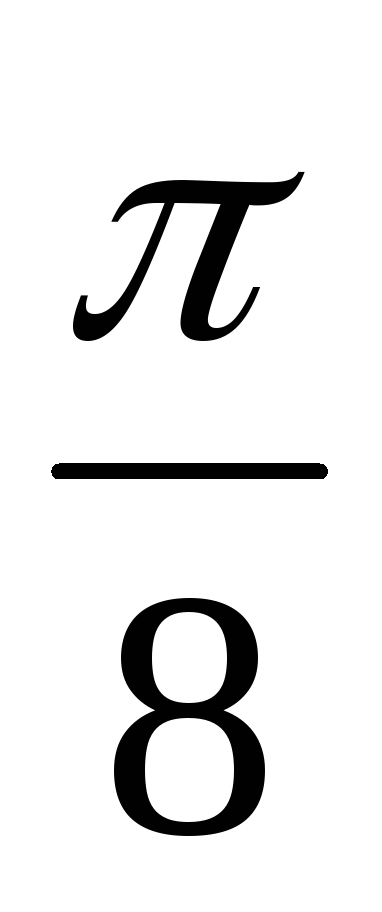
2. Найти каноническое уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная ось абсцисс – с полярной осью, и по уравнению определить тип линии.

Решение:

Т.к. полярный радиус неотрицателен, т.е. то откуда заключаем что

Составим вспомогательную таблицу, придавая значения через промежуток , начиная от =0

	1	0.924	0.707	0.383	0	-0.383	-0.383	0	0.383	0.707	0.924	1
	0.8	0.84	0.97	1.27	2	4.70	4.70	2	1.27	0.97	0.84	0.8

При

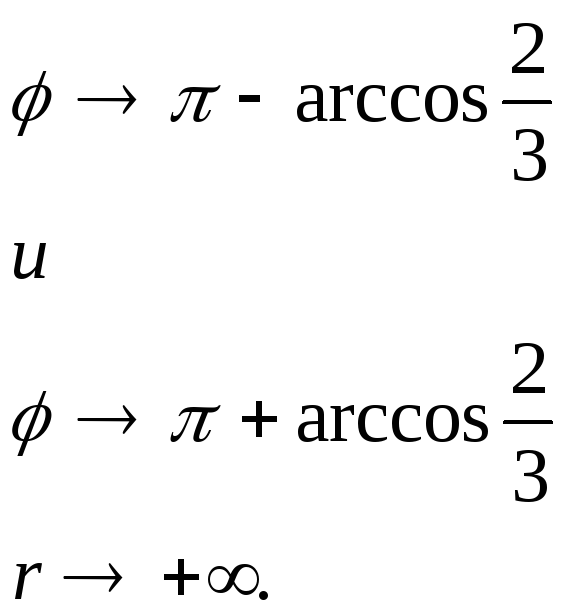
_{Для построения кривой на луче, проведенном из полюса под углом , откладываем соответствующее значение полярного радиуса и соединяем полученные точки.}

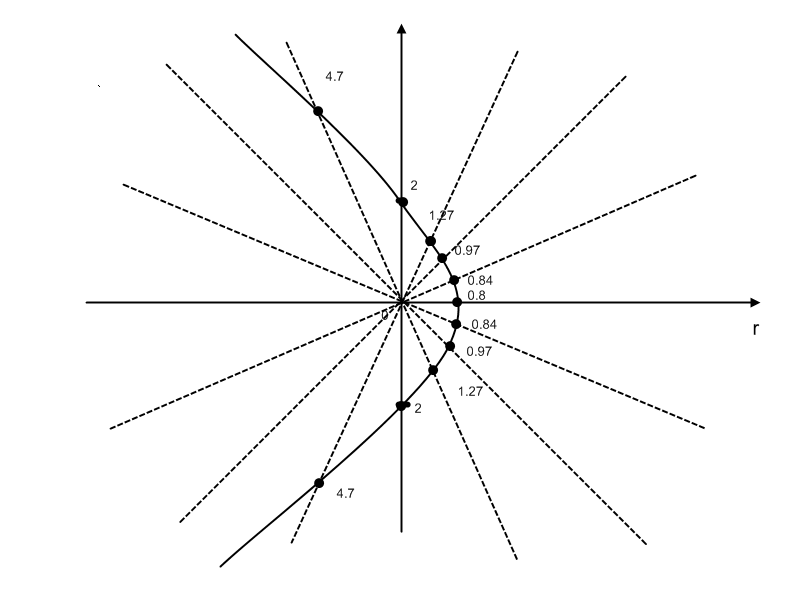
2. Найдем уравнение кривой 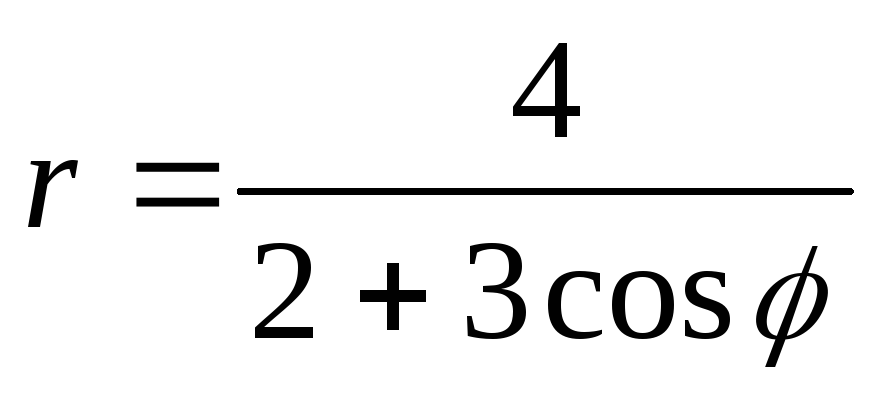в прямоугольной системе координат.

Для этого заменим и их выражениями через и по формулам 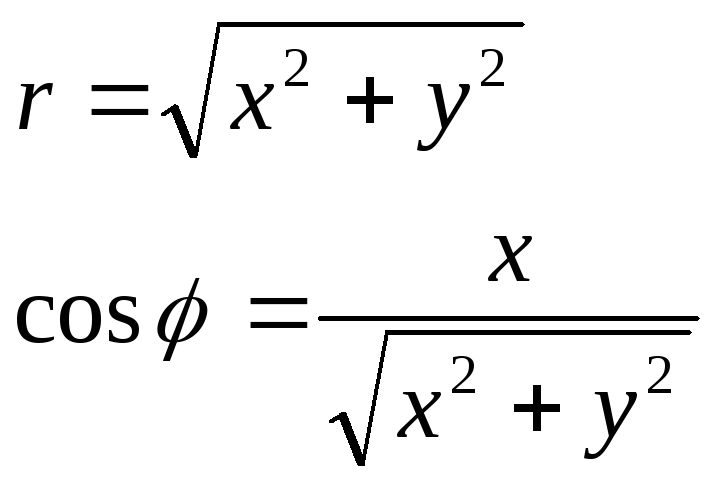Итак, получается:

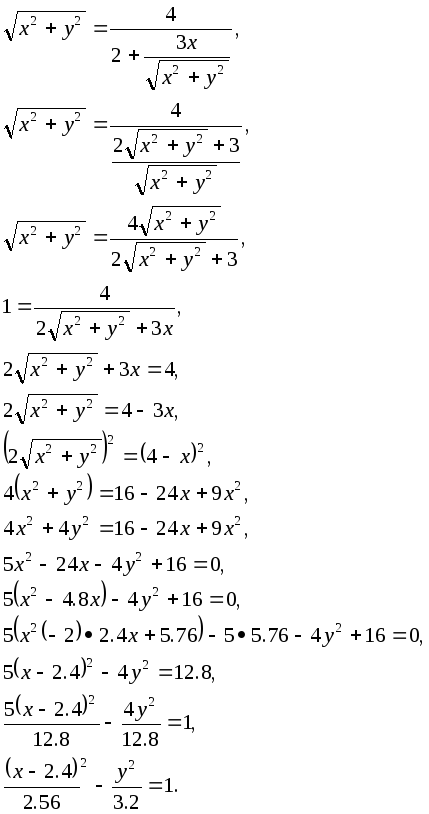
Как видим полученное уравнение уравнение гиперболы.

№103

Найти указанные пределы, не пользуясь правилом Лопиталя.

а)

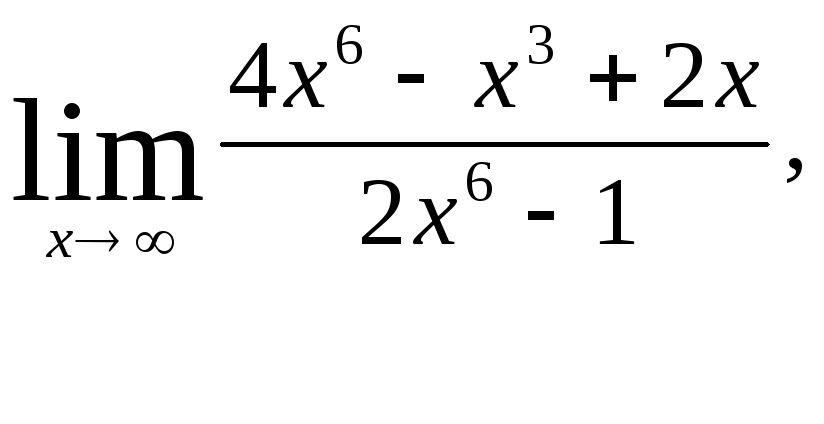
б)

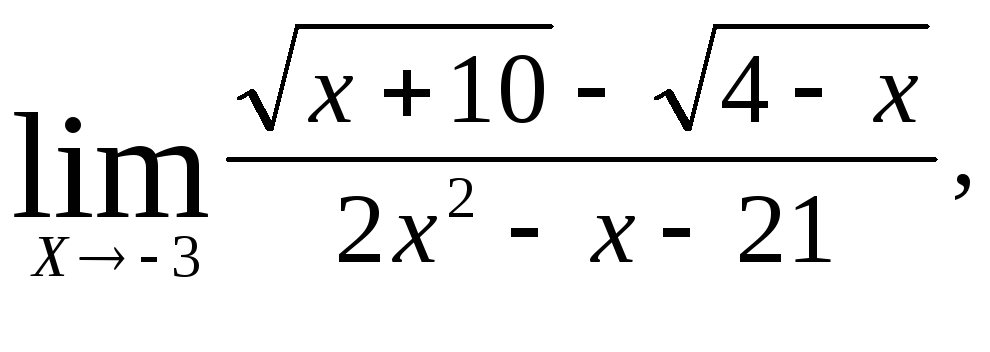
в)

Решение:

а) Разделим числитель и знаменатель на высшую степень x, т.е. на

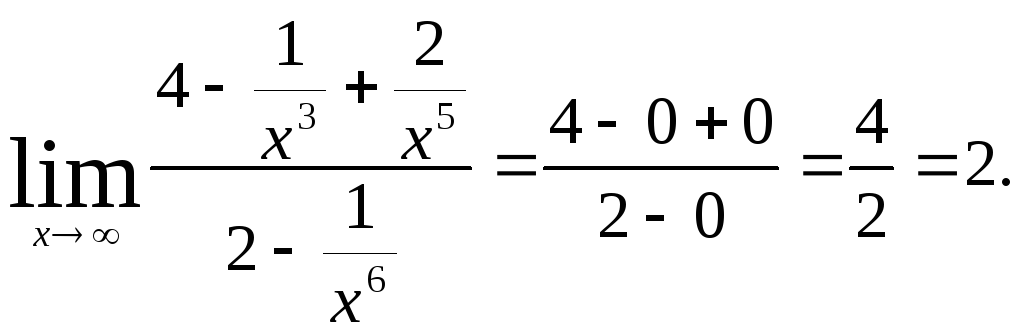
б)

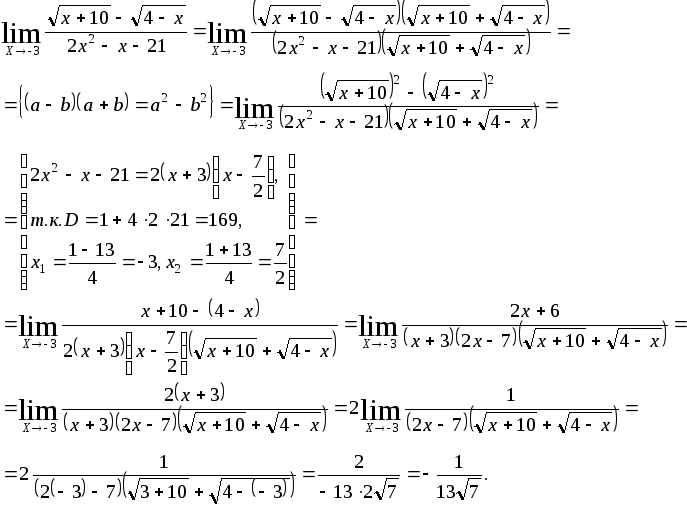
в)

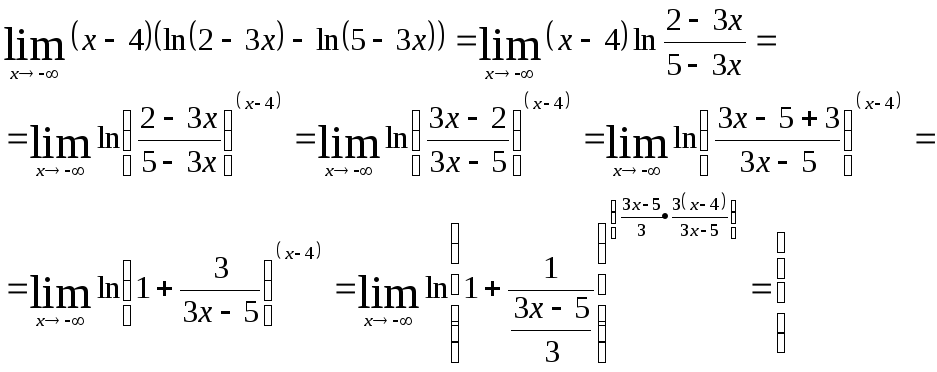
Воспользуемся вторым замечательным пределом

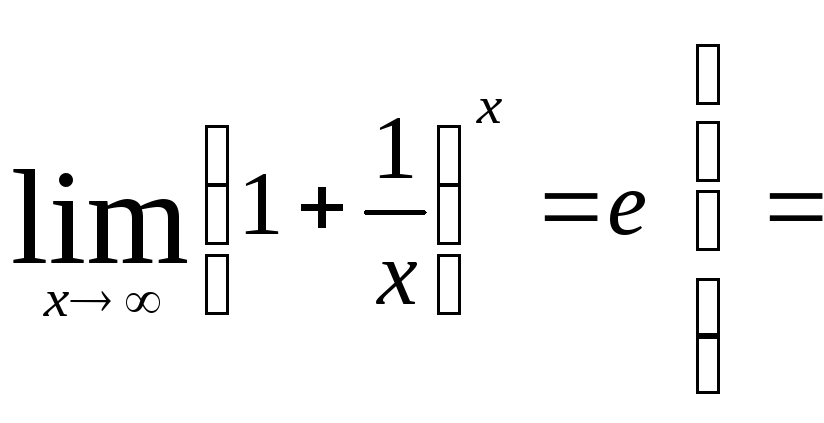
Ответ: а) 2, б) , в)1.

№113.

Найти указанные пределы, используя эквивалентные бесконечно малые функции.

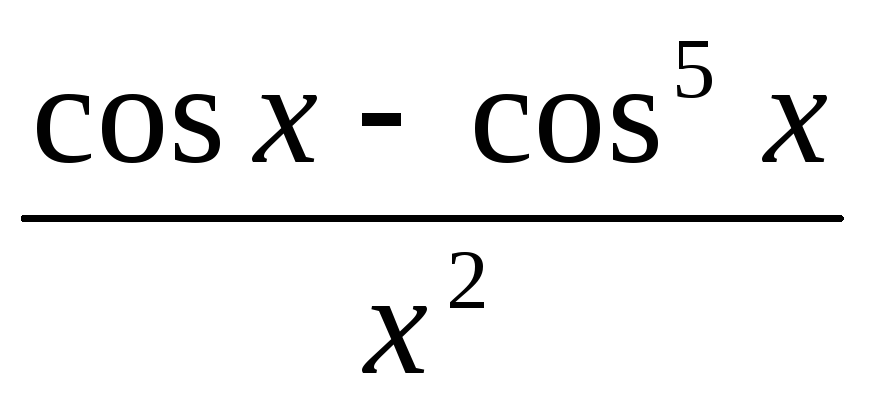1. , 2)

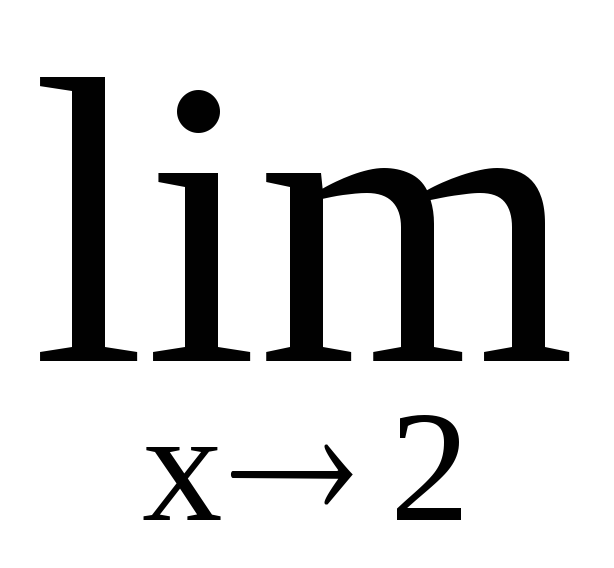
Решение:

1) = = = = =

= { при х 0 sinх} = = cosх · (1+cos²х) = =cos0 ·(1+ cos²0) = 1·(1+1²) = 2

2) = = = {пусть х-2= t, тогда х = 2+t, 3х- -5=3(2+t)-5=1+3t, х+3 = t+5, х²+1 = (2+t)² +1 = t²+4t+5} = = {при t0 ln(1+t)t} =

= = {при t0 tgtt} = =

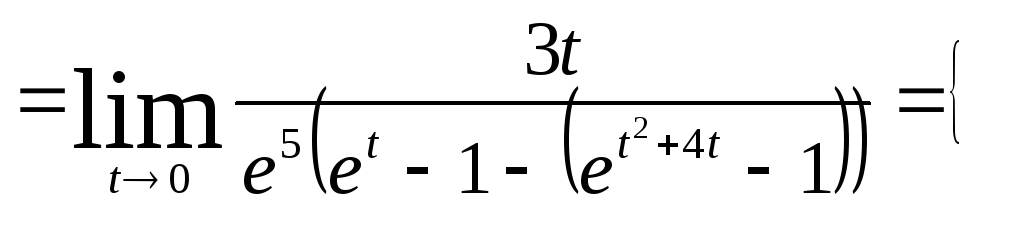при

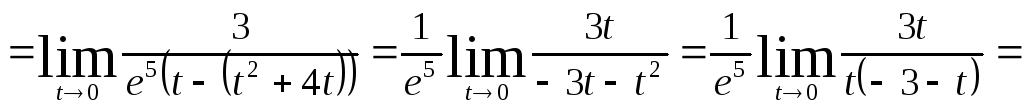
Ответ: 1) 2, 2) .

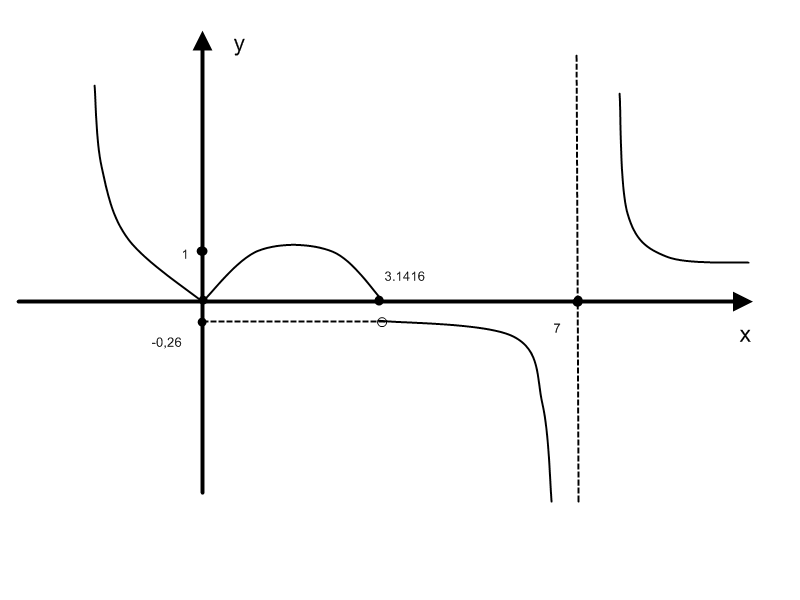
№123

Задана функция _{различными аналитическими выражениями для различных интервалов изменения аргумента. Найти точки разрыва функции, если они существуют, и установить их тип. Сделать чертеж.}

_{Решение:}

_{Поскольку в точке - точка разрыва функции. Исследуем характер разрыва. Найдем односторонние пределы функции в точке .}

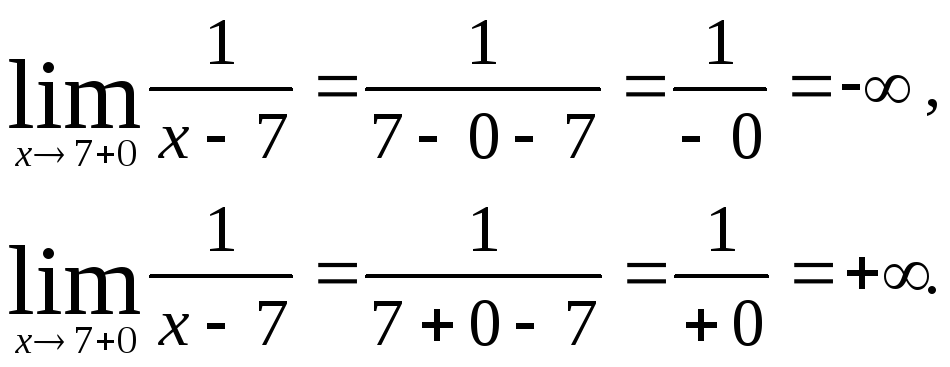
_{Т.к. оба предела равны} , то - точка разрыва второго рода.

Разрыв возможен также в точках и , в которых меняется аналитическое задание функции.

Найдем односторонние пределы функции в точке .

Т.к. то в точке функция является непрерывной.

Рассмотрим точку

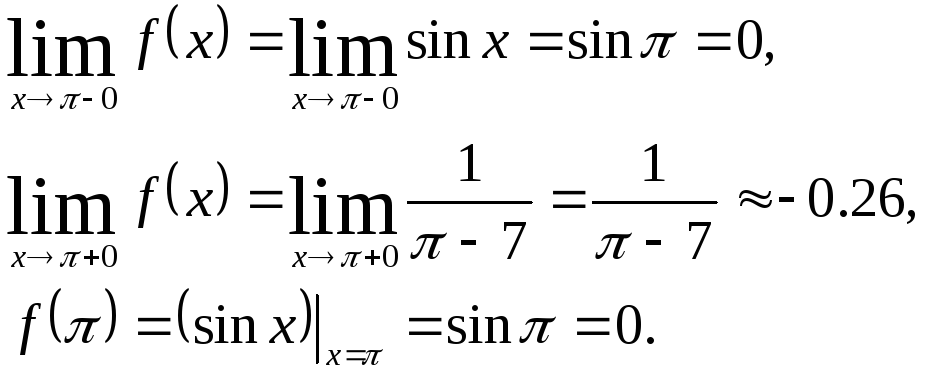
Т.к. односторонние пределы конечны, но не равны между собой, то - точка разрыва первого рода.