
ВМ Контрольна 3 вариант 8
.docБелорусский государственный университет информатики и радиоэлектроники
Факультет заочного и дистанционного обучения
Контрольная работа №3
по математике
108. Построить график функции
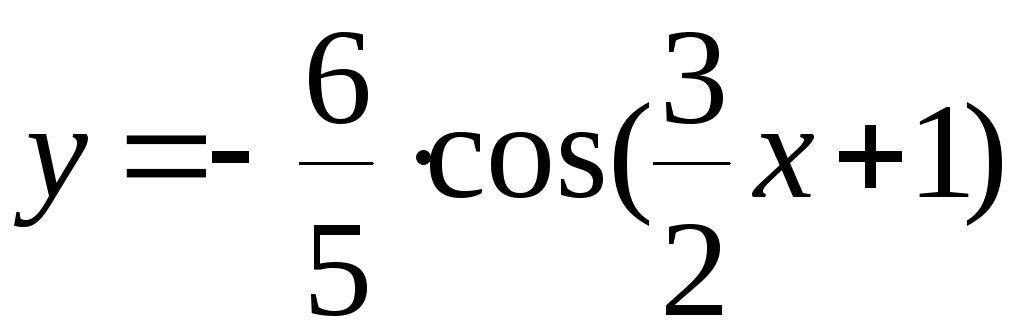 преобразованием графика функции
преобразованием графика функции
![]() .
.
Строим пошагово из функции
![]() функцию
функцию
 ,
для этого:
,
для этого:
-
Строим график функции
 :
:

-
Строим график функции
 сжатием
первого графика в 3/2 раза к оси Oy:
сжатием
первого графика в 3/2 раза к оси Oy:
-
Строим график функции
 ,
сдвинув предыдущий графи вдоль оси Ох
в отрицательном направлении на 1:
,
сдвинув предыдущий графи вдоль оси Ох
в отрицательном направлении на 1:

-
Строим график функции
 ,
для чего растянем предыдущий график
вдоль оси Оу в 6/5 раз (6/5>1):
,
для чего растянем предыдущий график
вдоль оси Оу в 6/5 раз (6/5>1):

-
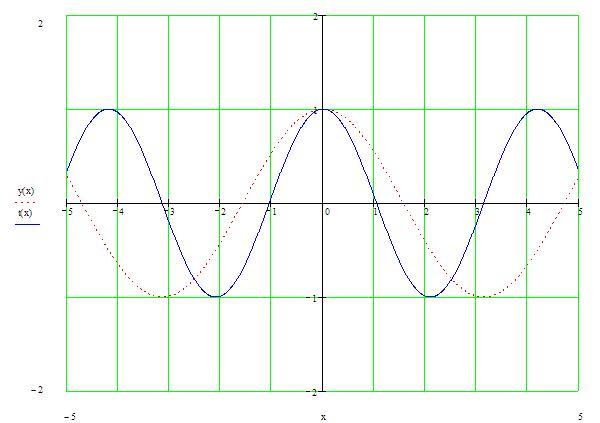
Строим конечный график
 зеркальным отображением предыдущего
графика относительно оси Оу:
зеркальным отображением предыдущего
графика относительно оси Оу:

118. Дана функция
 на отрезке
на отрезке
![]() .
Требуется: 1) построить график функции
в полярной системе координат по точкам,
давая значения
через промежуток /8,
начиная от =0; 2)
найти уравнение полученной линии в
прямоугольной декартовой системе
координат, начало которой совпадает с
полюсом, а положительная полуось абсцисс
– с полярной осью, и по уравнению
определить, какая это будет линия.
.
Требуется: 1) построить график функции
в полярной системе координат по точкам,
давая значения
через промежуток /8,
начиная от =0; 2)
найти уравнение полученной линии в
прямоугольной декартовой системе
координат, начало которой совпадает с
полюсом, а положительная полуось абсцисс
– с полярной осью, и по уравнению
определить, какая это будет линия.
1)
-










r
1
1,03
1,11
1,26
1,5
1,85
2,32
2,79
3
-








r
2,32
1,85
1,5
1,26
1,11
1,03
1

2) Перейдем от полярных координат к декартовым. Для этого воспользуемся формулами:
![]() (1)
(1)
![]() (2)
(2)
Подставив (1) и (2) в
 получаем:
получаем:

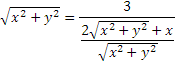
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Полученное уравнение – уравнение эллипса.
128. Найти предел:
а)
 (вычисляем по коэффициентам при
старших степенях)
(вычисляем по коэффициентам при
старших степенях)
б)


в)

г)
 =
=![]()
138. Заданы функция ![]() и два значения аргумента x1=3
и x2=1. Требуется: 1)
установить, является ли данная функция
непрерывной или разрывной для каждого
из данных значений аргумента; 2) в случае
разрыва функции найти ее пределы при
приближении к точке разрыва слева и
справа; 3) сделать схематический чертеж.
и два значения аргумента x1=3
и x2=1. Требуется: 1)
установить, является ли данная функция
непрерывной или разрывной для каждого
из данных значений аргумента; 2) в случае
разрыва функции найти ее пределы при
приближении к точке разрыва слева и
справа; 3) сделать схематический чертеж.
![]() => в т.х1=3
функция f(x)
непрерывна
=> в т.х1=3
функция f(x)
непрерывна
![]() => т.x2=1
является точкой разрыва, т.к. f(x)
в ней не определена
=> т.x2=1
является точкой разрыва, т.к. f(x)
в ней не определена
Определим вид точки разрыва, для чего вычислим односторонние пределы:
![]()
![]()
Так как оба односторонних предела равны бесконечности, то т.х2=1 является точкой разрыва второго рода бесконечного скачка.
1
х y 0









148. Различными аналитическими выражениями для различных областей изменения независимой переменной задана функция. Найти точки разрыва функции, если они существуют. Сделать чертеж.

π/4







Функции y=x,
y=tgx,
y=2
непрерывны на соответствующих интервалах
(-∞; 0]; (0; ![]() ];
(
];
(![]() ;
+∞).
;
+∞).
Проверим точки
х1=0
и х2=
![]() :
:

f(0)=tg0=0
f(0)=0=0
Следовательно х1 – точка непрерывности

Т.к. существуют оба односторонних предела, но они не равны, то т.х2 – точка разрыва первого рода (конечного скачка)


