1 курс к.р.3 вар

Учреждение образования

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет заочного и дистанционного обучения

Специальность ПОИТ

Контрольная работа

по Высшей математике №3

Вариант № 9

Зачётная книжка №

Электронный адрес

Минск 2011

№89

Выделив в заданной функции полный квадрат, получить уравнение параболы и построить её график.

Дано: .

Решение:

Уравнение параболы, полученной из параболы путём переноса вдоль оси на 8 единиц вниз; вдоль оси на 4 единицы влево и сжатия в 3 раза.

Вершина параболы

№99

Задана функция на отрезке . Требуется: 1) построить график функции в полярной системе координат по точкам, давая аргументу значения через промежуток ; 2) найти каноническое уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить тип линии.

Дано:

_{Решение:}

0

Приведём уравнение к каноническому виду:

;

; ;

; ;

;

;

;

;

;

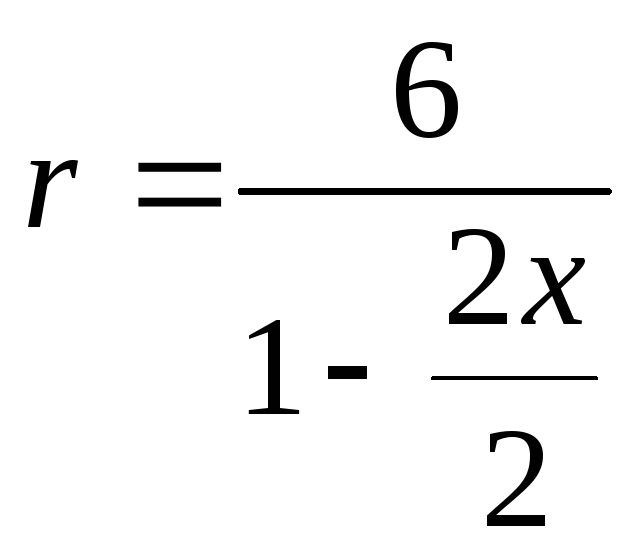— уравнение гиперболы.

№109

Найти указанные пределы, не пользуясь правилом Лопиталя.

Дано:

1) ; 2) ; 3) .

1) .

2) .

Разложим знаменатель на множители:

; ; ;

3) 

_№119

Найти указанные пределы, используя эквивалентные бесконечно малые функции.

_Дано: 1) ; 2) .

Решение:

1).

2) .

_№129

Задана функция различными аналитическими выражениями для различных интервалов изменения аргумента. Найти точки разрыва функции, если они существуют, и установить их тип. Сделать чертёж.

_Дано:

_{Решение:}

_{; ;— нет разрыва.}

_;

_{— точка разрыва I рода.}

_{Функция при в точке имеет разрыв II рода, т.к.}