BM Контрольная работа №3. Вариант №8

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра программного обеспечения информационных технологий

Факультет НиДО

Специальность ПОИТ

Контрольная работа № 3

по дисциплине «Высшая математика»

Вариант № 8

Выполнил студент: ******

группа ******

Зачетная книжка № ******-28

Электронный адрес ******@****.***

Минск 2010

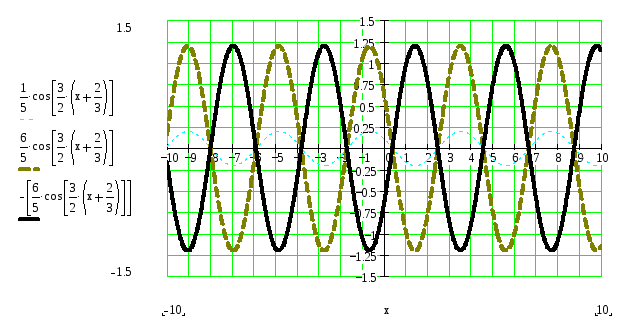
Задача 108

Построить график функции преобразованием графика функции

Решение:

1) Чтобы построить преобразованием , приведем к виду :

2) Строим график функции

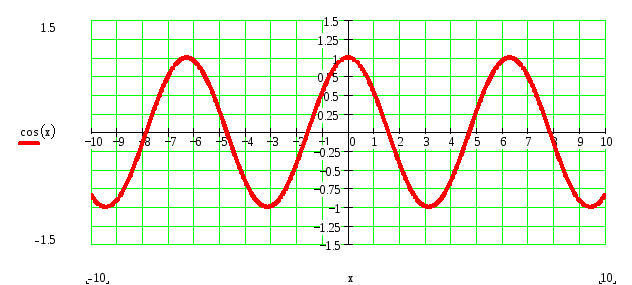
3) Строим график функции сдвинув график вдоль оси ОХ в отрицательном направлении на :

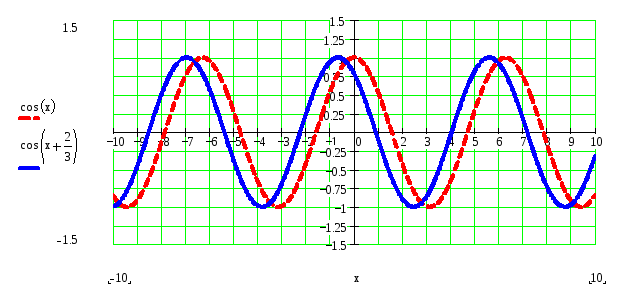
4) Строим график функции сжатием графика в 3 раза к оси ОY:

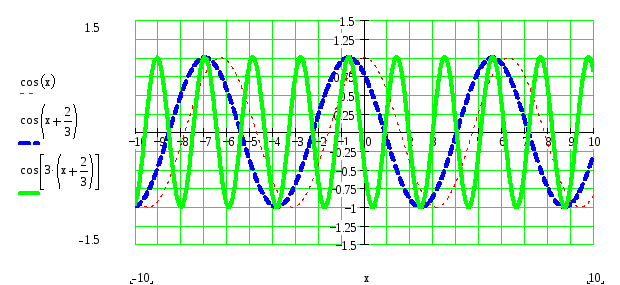
5) Строим график функции растягиванием графика в 2 раза от оси ОY:

6) Строим график функции сжатием графика в 5 раз к оси ОX:

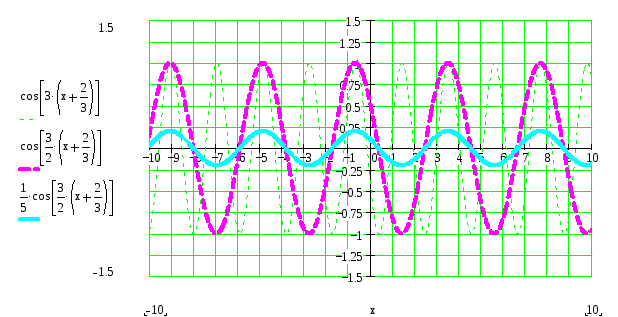
7) Строим график функции растягиванием графика в 6 раз от оси ОX:

8) Строим график функции симметрично отразив график относительно оси ОX:

Задача 118

Дана функция на отрезке . Требуется: 1) построить график функции в полярной системе координат по точкам, давая значения через промежуток , начиная от ; 2) найти уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить, какая это будет линия.

Решение:

1) Построить график функции в полярной системе координат по точкам, давая аргументу значения через промежуток .

Составим таблицу значений аргумента и функции:

	1	1,026	1,108	1,259	1,5	1,855	2,32	2,788	3

	2,788	2,32	1,855	1,5	1,259	1,108	1,026	1

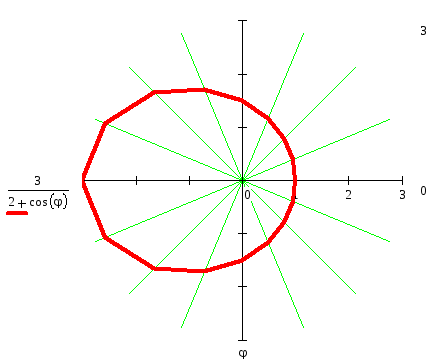
Для вычерчивания линии проведем радиусы-векторы, соответствующие углам , взятым с интервалом . На каждом из этих радиусов-векторов откладываем отрезки, равные значению r при соответствующем значении из таблицы . Соединяя точки, являющиеся концами этих отрезков, получаем график данной линии:

2) найти уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить, какая это будет линия.

Подставляя и в уравнение, имеем:

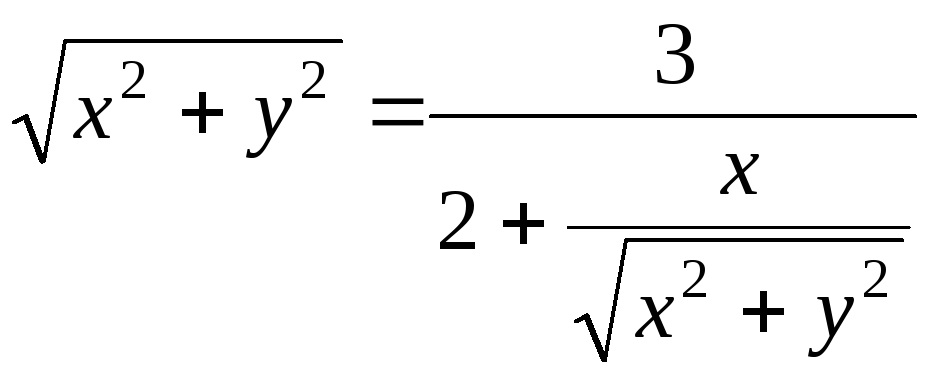
Полученное уравнение – это каноническое уравнение эллипса с центром в точке и полуосями , .

Задача 128

Найти указанные пределы, не пользуясь правилом Лопиталя.

а) б)

в) г)

Решение:

а)

Подстановка предельного значения аргумента приводит к неопределённости вида . Разделим числитель и знаменатель на старшую степень аргумента, т.е. на . Получим

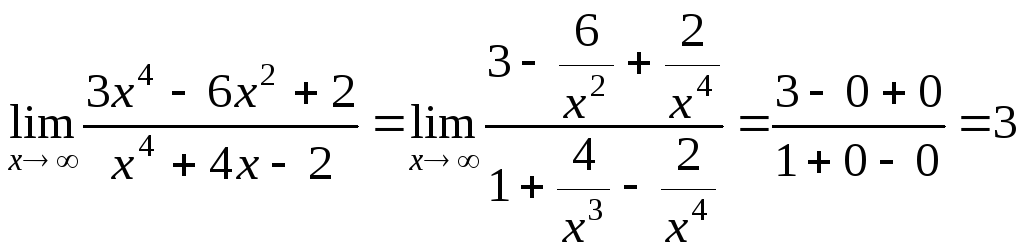
так как при функции , и – бесконечно малые функции.

б)

Пределы числителя и знаменателя при равны нулю, т.е. имеем неопределенность . Избавимся от иррациональности в знаменателе, умножив числитель и знаменатель на:

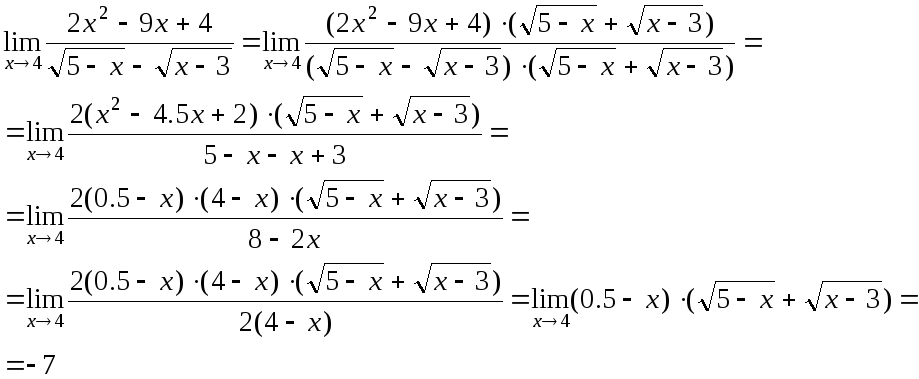
в)

Пределы числителя и знаменателя при равны нулю, т.е. имеем неопределенность . Используя формулы , и получим:

г)

Подстановка приводит к неопределенности . Сделаем замену переменной , принимая во внимание, что . Тогда

– второй замечательный предел.

Задача 138

Заданы функция и два значения аргумента и . Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы при приближении к точке разрыва слева и справа; 3) сделать схематический чертеж.

, , .

Решение:

1) , следовательно в точке непрерывна.

, следовательно точка разрыва, так как в этой точке не определена.

2) Определим вид точки разрыва, для чего вычислим односторонние пределы:

, так как при

, так как при

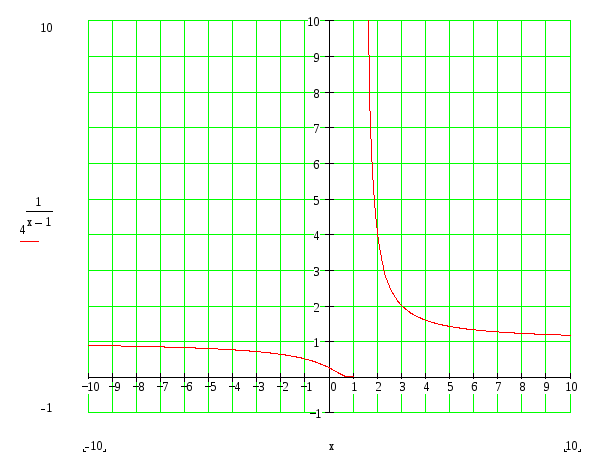
– точка разрыва второго рода

3)

Задача 148

Задана функция различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Сделать чертеж.

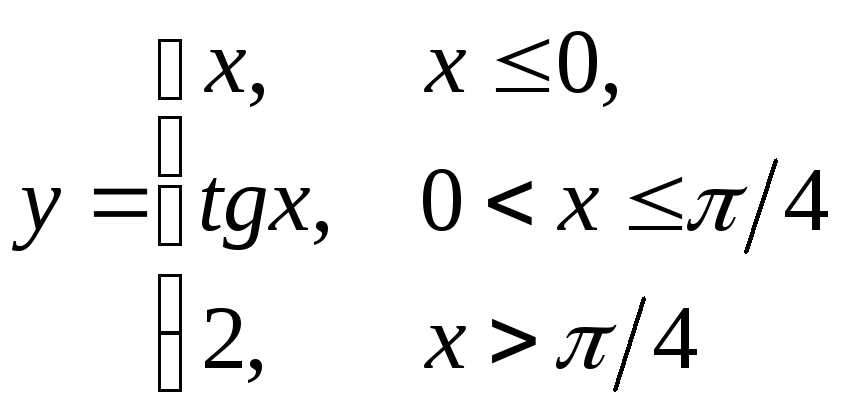
Решение:

непрерывна на интервале

непрерывна на интервале

непрерывна на интервале

и – подозрительные точки

Вычислим односторонние пределы в подозрительных точках:

В точке – непрерывна, так как существуют правый и левый пределы, они равны и равны значению функции в этой точке;

Так как существуют правый и левый пределы, но они не равны, то точка разрыва первого рода (конечного скачка)