KP №2

Учреждение образования

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет заочного и дистанционного обучения

Специальность ПОИТ

Контрольная работа

по Высшей математике №2

Вариант № 5

Минск 2010

№45

Доказать совместность данной системы линейных уравнений и решить её тремя методами: 1) по формулам Крамера; 2) методом Гаусса; 3) средствами матричного исчисления (с помощью обратной матрицы).

Решение

Система, имеющая хотя бы одно решение, называется совместной. Необходимым и достаточным условием совместности системы линейных уравнений является

Критерий Кронекера–Капелли. Для того чтобы линейная система была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы. Если же эти ранги не равны, то система несовместна.

Исследование на совместность по критерию Кронекера-Капелли:

Для этого составим расширенную матрицу системы для определения её ранга и ранга матрицы коэффициентов:

.

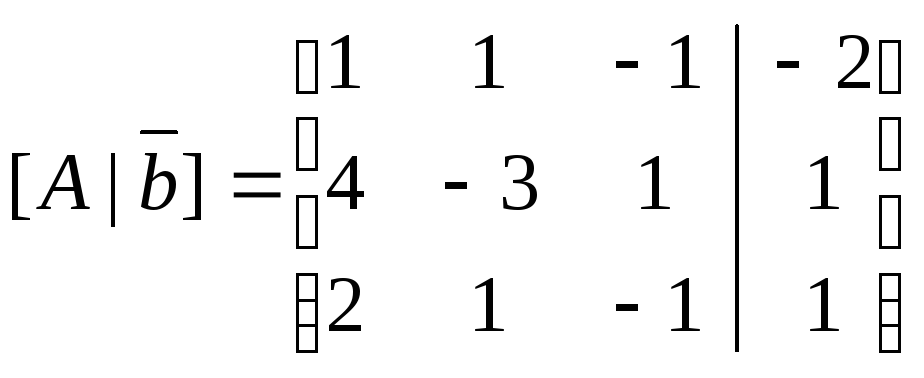Находим ранг r расширенной матрицы:

.

Отсюда , следовательно данная линейная система совместна.

1. Решить систему уравнений по формулам Крамера:

Решение

Составим матрицу коэффициентов (основную матрицу системы) и найдем её определитель:

.

Так как определитель отличен от нуля, то система совместна и имеет единственное решение. Вычисляем определители

; ; ,

которые составляем из матрицы коэффициентов путем поочередной замены каждого из столбцов на столбец правой части системы.

Далее по формулам Крамера вычисляем:

Таким образом, система имеет единственное решение , , .

2)При решении системы линейных уравнений методом Гаусса действия производятся над расширенной матрицей

Решение

Составим расширенную матрицу системы: .

Теперь приведём её путем элементарных преобразований к треугольному или трапециевидному виду. Для этого прибавим ко 2‑й строке 1‑ю, умноженную на , к 3‑й строке прибавим 1‑ю, умноженную на . Получим: .

.

Таким образом, ранги основной и расширенной матриц равны 3. Система совместна и имеет единственное решение. Она сводится к эквивалентной системе линейных уравнений

Отсюда, подставляя во второе уравнение, получим , а из первого уравнения . Итак, , , .

2. применение матричного метода рассмотрим на примере системы

Решение

Определитель основной матрицы системы , значит, система совместна и для матрицы коэффициентов существует обратная матрица. Находим решение по формуле или

,

где , алгебраические дополнения элементов матрицы А:

Таким образом, обратная матрица к основной матрице системы имеет вид

.

Значит, матричное решение системы имеет вид

Отсюда следует, что , , .

Задача 55

Исследовать на совместность систему линейных уравнений

и в случае совместности найти её общее решение.

Решение

Для исследования совместности применим критерий Кронекера-Капелли. Для этого составим расширенную матрицу системы для определения её ранга и ранга матрицы коэффициентов:

.

Находим ранг r расширенной матрицы:

~ ~ ;

– система линейных уравнений несовместна и решений не имеет. Также последняя строка эквивалентной матрицы, полученной путем элементарных преобразований, соответствует:

– что не верно.

Задача 65

Найти собственные значения и собственные векторы линейных преобразований, заданных в некотором базисе матрицами:

A=

Решение

Составляем характеристическое уравнение матрицы А и находим его корни:

Так как все корни оказались действительными числами, то они являются собственными значениями матрицы А.

Так при система примет вид:

;

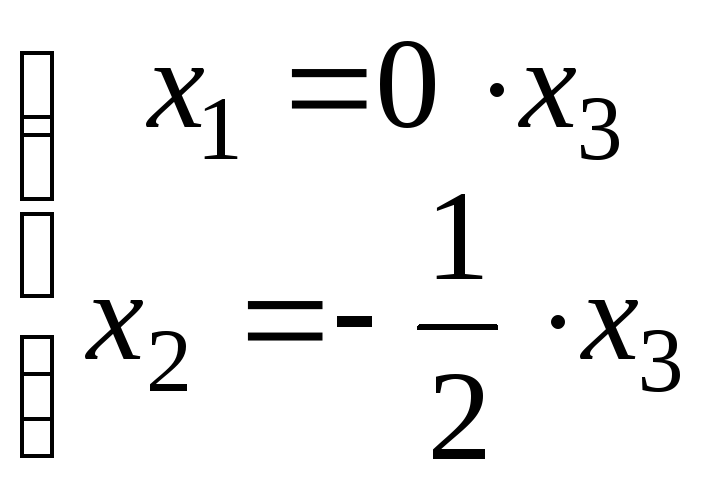Следовательно, собственный вектор, соответствующий собственному значению , имеет вид: - где x₃ – произвольное действительное число, не равное нулю. Положив его, в частности, равным единицы, получим собственный вектор в виде ;

Аналогично при система примет вид:

;

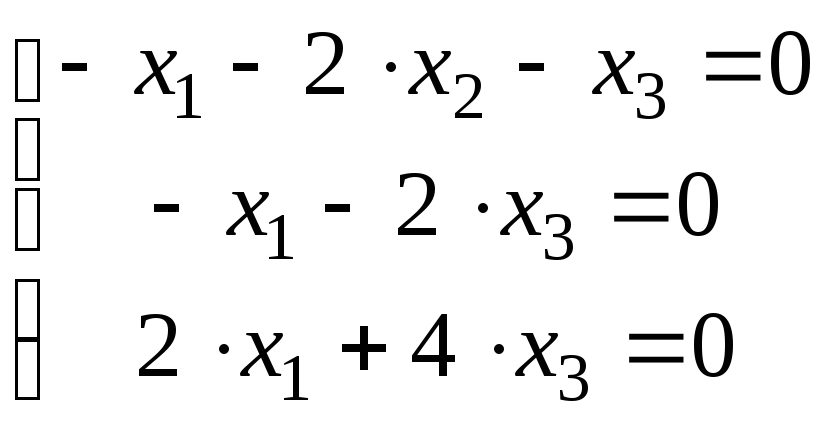
Значит, собственному значению соответствует собственный вектор

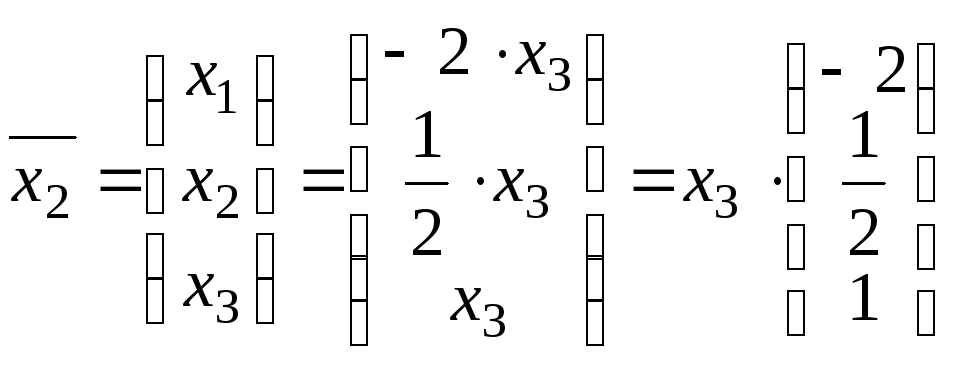или ;

При система имеет вид:

;

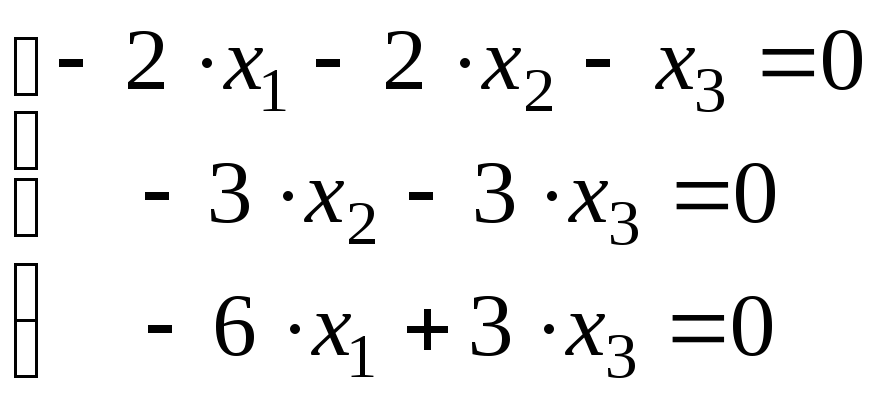
Значит, собственному значению соответствует собственный вектор

или .

Задача 75

Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка и построить ее в декартовой системе координат.

.

Составим матрицу данной квадратичной формы ;

Составим характеристическое уравнение матрицы A и найдем ее собственные значения и собственные векторы:

;

Значит, собственные векторы будут иметь вид:

для x₁ = –x₂ ;

для x₁ = x₂ ;

Нормируем собственные векторы:

; ;

Матрица перехода к новому базису будет иметь вид ;

Введем замену переменных и подставим эти выражения в исходное уравнение кривой:

; ; тогда:

;

Преобразуя полученное выражение, получим:

;

;

;

Введем еще одну замену и подставим в полученное выражение:

; ;

;

;

;

Полученное уравнение является каноническим уравнением эллипса, с центром в начале, смещенной, системы координат O''X''Y'', с полуосями и .