Высшая математика Контрольная №1 Вариант №3

№ 3 Даны четыре вектора,,и заданные в прямоугольной декартовой системе координат. Требуется:

1) вычислить скалярное произведение ,

2) вычислить векторное произведение

3) показать, что векторы , , образуют базис и найти координаты вектора в этом базисе.

Решение:

1)Найдем вектор .

Для этого умножим координаты вектора на 2 и от полученного вектора вычтем вектор . В результате вычитания получим:

Так как скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат, то

2) Найдем вектор :

Векторное произведение двух векторов:

=

.

Окончательно получаем, что вектор, равный векторному произведению , имеет координаты

3)Составим определитель из координат векторов , , и вычислим его

=

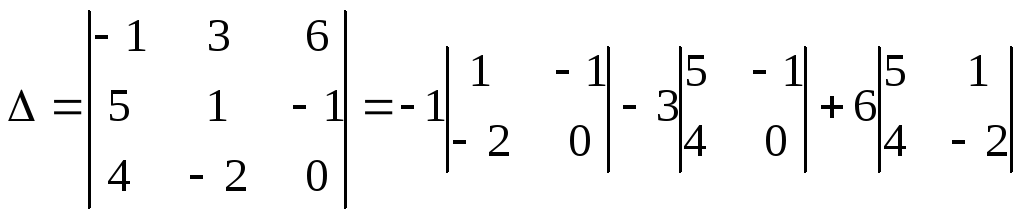Т.к. , то система векторов , , линейно независима. Следовательно, векторы , , образуют базис пространства и вектор единственным образом разлагается по векторам этого базиса или

.

Приравнивая соответствующие координаты двух равных векторов, получаем следующую систему:

Полученную систему решим по формулам Крамера.

, , ,

где -94

, , - определители, которые получаются из определителя заменой соответственно 1-го, 2-го, 3-го столбца на столбец свободных членов.

Найдем ,,

Следовательно,

,

Следовательно, т.е. вектор в базисе , , имеет координаты (3,-2,-1)

№13. Даны координаты вершин пирамиды . Найти: 1) длину ребра ; 2) уравнение прямой ; 3) угол между рёбрами и ; 4) уравнение плоскости ; 5) угол между ребром и гранью ; 6) уравнение высоты, опущенной из вершины на грань ; 7) площадь грани ; 8) объём пирамиды; 9) сделать чертёж.

Решение:

1)Обозначим

Длину ребра запишем по форме:

(лин. ед)

2) Уравнение прямой запишем по формуле:

.

3) Угол между ребрами и равен углу между векторами и

Из скалярного произведения векторов и имеем:

Найдем координаты векторов :

Следовательно

=

4) Найдем уравнение плоскости по формуле уравнения плоскости, проходящей через три заданные точки. =

Разрыв скобки, получим общее уравнение плоскости :

5) Угол между ребром и гранью найдем по формуле:

Уравнение плоскости :, значит,

=значит,.

6)Уравнение высоты, опущенной из вершины на грань найдем по формуле

В данном случае а направляющий вектор – это вектор , т.к. нормальный вектор плоскости является направляющим вектором рассматриваемой высоты.

Итак, искомое уравнение высоты примет вид:

7)Найдем площадь грани

Грань - треугольник, а из векторного произведения двух векторов мы знаем, что длинна вектора равна площади параллелограмма, построенного на этих векторах. След-но, площадь треугольника будет вычисляться по формуле:

Значит,

8) Вычислим объем пирамиды . Из смешанного произведения трех векторов мы знаем, что , т.е. объем пирамиды равен 1/6 объема параллелепипеда, построенного на векторах ,,.

В свою очередь объем параллелепипеда равен модулю смешанного произведения этих векторов. Найдем смешанное произведение векторов ,,. Их координаты мы уже знаем.

(,,)=

№ 23 Найти координаты точки , симметричной точке относительно прямой

Решение:

Искомая точка является вторым концом отрезка , для которого серединой будет точка R – проекция точки на данную прямую. Найдем точку R.

Точка R является точкой пересечения данной прямой и плоскости, проведенной через точку перпендикулярную этой прямой. Ур-ние указанной плоскости ищем в виде:

- направляющий вектор рассматриваемой плоскости прямой нормальный вектор плоскости .

Итак, ур-ние плоскости:

Находим точку пересечения данной прямой и полученной плоскости, уравнение прямой в параметрическом виде имеет вид: Тогда

Поскольку R – середина , то

.

Итак,

№ 33 Составить уравнение линии, для каждой точки которой отклонение расстояние до начала координат к расстоянию до прямой 3x+16=0 равно 0.6

Решение: Пусть – произвольная точка искомой линии,

проекция точки на прямую

По условию

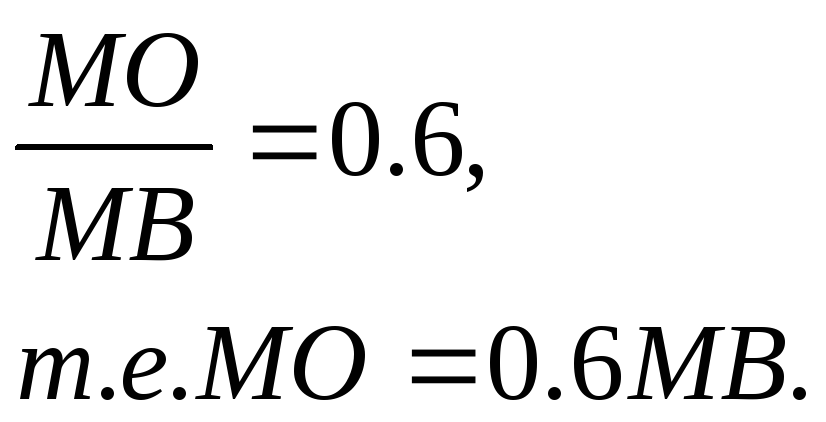
С другой стороны, по формуле расстояние между двумя точками, получаем:

Подставляя эти выражения в равенство

- уравнение эллипса