
ВМ Контрольна 1 вариант 1
.doc
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра высшей математики
Факультет ФНиДО
Специальность ПОИТ
Контрольная работа № 1
по дисциплине «Высшая математика»
Вариант № 1
Выполнил студент: Янченко А.А.
группа 191003
Зачетная книжка № 191003-31
Барань 2011
Задача1
Даны
четыре вектора![]() ;
;![]() ;
;![]() ;
;![]() ,
заданные в декартовой системе координат.
Требуется: 1) вычислить скалярное
произведение
,
заданные в декартовой системе координат.
Требуется: 1) вычислить скалярное
произведение
![]() ;
2) вычислить векторное произведение
;
2) вычислить векторное произведение
![]() ;
3) показать, что векторы
;
3) показать, что векторы
![]() образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
![]() в этом базисе.
в этом базисе.
Решение
1) Найдем вектор
![]()
![]() 2(
2(![]() )
= (
)
= (![]() )
= (4; 2; -2).
)
= (4; 2; -2).
Тогда
![]() (f1,
f2, f3)
= (4 - (-2); 2 - 5; - 2 - 3) = (6; -3; -5).
(f1,
f2, f3)
= (4 - (-2); 2 - 5; - 2 - 3) = (6; -3; -5).
Скалярное произведение векторов
![]() найдем
по формуле:
найдем
по формуле:
![]() =
=![]() = b1f1
+ b2f2
+ b3f3
= 1
6 + 3
(-3) + 0
(-5) = 6 - 9 + 0 = -3
= b1f1
+ b2f2
+ b3f3
= 1
6 + 3
(-3) + 0
(-5) = 6 - 9 + 0 = -3
б) Найдем вектор
![]()
![]() 3(1; 3; 0) = (3
1; 3
3; 3
0) = (3; 9; 0)
3(1; 3; 0) = (3
1; 3
3; 3
0) = (3; 9; 0)
Тогда
![]() (е1,
е2, е3) = (2 - 3; 1- 9; -1 – 0) = (-1; - 8;
-1)
(е1,
е2, е3) = (2 - 3; 1- 9; -1 – 0) = (-1; - 8;
-1)
Векторное произведение векторов
![]() найдем
по формуле:
найдем
по формуле:

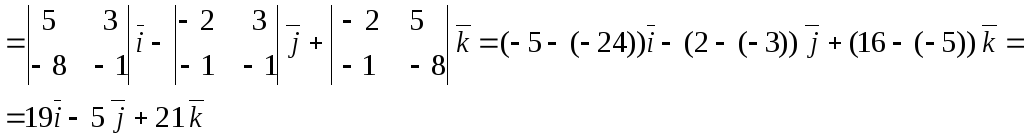 3)
Найдем смешанное произведение векторов
3)
Найдем смешанное произведение векторов
![]() :
:

Т.к.
![]() ≠
0, значит данные векторы не компланарны.
Таким образом, они линейно независимы
и образуют базис.
≠
0, значит данные векторы не компланарны.
Таким образом, они линейно независимы
и образуют базис.
Найдем координаты вектора
![]() d
в этом базисе.
d
в этом базисе.
![]()
Это равенство равносильно следующим равенствам:
2x + 1 y - 2 z = - 6 2x + у - 2z = - 6
1 x + 3y + 5z = 20 x + 3y + 5z = 20
-1 x + 0 y + 3z = 10 - x + 3z = 10
Решим данную систему. Из 3-го уравнения получаем х = 3z - 10. Подставим полученное выражение для x в 1-ое уравнение:
2 (3z – 10) + y – 2z = - 6 у = - 4z + 14
Подставим полученные выражения для x и z вo 2-oе уравнение:
3z - 10 + 3(- 4z + 14) + 5z = 20
z = 3
x = 3 3 – 10 = - 1
y = - 4 3 + 14 = 2
Тогда
![]()
Таким образом, вектор
![]() в
базисе
в
базисе
![]() имеет координаты х = - 1; у = 2; z
= 3
имеет координаты х = - 1; у = 2; z
= 3
Ответ: 1) - 3; 2)
![]() ;
3)
;
3)
![]()
Задача 11
Даны координаты вершин пирамиды
![]() :
:![]() ,
,![]() ,
,
![]() ,
,![]() .
Найти:
.
Найти:
1) длину
ребра
![]() ;
;
2) уравнение
прямой
![]() ;
;
3) угол
между рёбрами
![]() и
и
![]() ;
;
4) уравнение
плоскости
![]() ;
;
5) угол
между ребром
![]() и гранью
и гранью
![]() ;
;
6) уравнение
высоты, опущенной из вершины
![]() на грань
на грань
![]() ;
;
7) площадь
грани
![]() ;
;
8) объём пирамиды;
9) сделать чертёж.
Решение
1) Найдем длину ребра А1А2 по формуле:

2) Уравнение прямой А1А2 напишем в виде уравнения прямой, проходящей через две точки А1 и А2:

![]() -
уравнение прямой А1А2.
-
уравнение прямой А1А2.
Вектор
![]() -
направляющий вектор прямой А1А2.
-
направляющий вектор прямой А1А2.
3) Угол между ребрами А1А2 и
А1А4 найдем как угол
между векторами
![]() :
:

![]() -
направляющий вектор прямой А1А4.
-
направляющий вектор прямой А1А4.
![]()
![]()
![]()
^
Следовательно, (А1А2, А1А4) = = arccos 0,906 0,436(рад) 25о
4) Найдем уравнение плоскости А1А2 А3 по трем точкам:


(x-3)( 10 + 0) – (y - 1)( - 8 - 12 ) + ( z - 4)(0 + 20) = 0
10(x-3) + 20(y - 1) + 20( z - 4) = 0
10x + 20y + 20z - 130 = 0
x + 2y + 2z - 13 = 0 – общее уравнение плоскости А1А2 А3.
![]() =
(A, B, C)
= (1; 2; 2) – нормальный вектор плоскости
А1А2 А3.
=
(A, B, C)
= (1; 2; 2) – нормальный вектор плоскости
А1А2 А3.
5) Найдем угол между гранью А1А2 А3 и ребром А1 А4:
 ,
где
,
где
A, B, C - координаты нормального вектора плоскости А1А2 А3 ,
![]() -
координаты направляющего вектора прямой
А1А4.
-
координаты направляющего вектора прямой
А1А4.
![]()
= arccin 0,356 = 0,364(рад) 20,85о
6) Найдем уравнение высоты, опущенной
из вершины
![]() на грань
на грань
![]() ;
по формуле:
;
по формуле:
![]() ,
,
где N(A, B,C) – нормальный вектор к плоскости А1А2 А3, являющийся направляющим вектором искомой высоты.
Имеем:
![]()
7) Найдем площадь грани А1 А2 А3.
![]()
![]()
![]()

![]()
![]()
8) Найдем объём пирамиды по формуле:
V =
![]() ,
,
где S- площадь грани А1 А2 А3, h – высота, опущенная из вершины А4.
Найдем длину высоты h как расстояние от точки А4 (0; 4; -1) до
плоскости А1 А2 А3:
![]()
![]()
9) Сделаем чертеж пирамиды:

Ответ: 1)![]() ;
2)
;
2)
![]() ;
3) 25о; 4) x
+ 2y + 2z
- 13 = 0;
;
3) 25о; 4) x
+ 2y + 2z
- 13 = 0;
5) 20,85о ; 6)
![]() ;
7) 15 (ед.кв.); 8)
;
7) 15 (ед.кв.); 8)
![]() (ед.куб.)
(ед.куб.)
Задача 21
Найти
координаты точки
![]() ,
симметричной точке
,
симметричной точке
![]() относительно прямой
относительно прямой
![]() .
.
Решение
Исходя из заданного уравнения прямой запишем ее параметрическое уравнение:
х = 4,5 + t
y = - 3 – 0,5t
z = 2 + t
Ее направляющим вектором будет вектор
![]() (1;
- 0,5; 1).
(1;
- 0,5; 1).
Проекция точки М (точка F) на заданную прямую имеет координаты:
F = (4,5 + t; - 3 – 0,5t; 2 + t)
Тогда вектор
![]() =
(хF
– хМ; уF
– уМ; zF
– zМ)
= (4,5 + t - 2; - 3 – 0,5t
– (-1); 2 + t – 1) = (t
+ 2,5; - 0,5t - 2; t
+ 1)
=
(хF
– хМ; уF
– уМ; zF
– zМ)
= (4,5 + t - 2; - 3 – 0,5t
– (-1); 2 + t – 1) = (t
+ 2,5; - 0,5t - 2; t
+ 1)
Т.к. направляющий вектор
![]() заданной прямой и вектор
заданной прямой и вектор
![]() перпендикулярны, то скалярное произведение
этих векторов будет равно нулю:
перпендикулярны, то скалярное произведение
этих векторов будет равно нулю:
![]()
![]() =
0 или
=
0 или
(t + 2,5) · 1 + (- 0,5t - 2) · (- 0,5) + (t + 1) · 1 = 0 2,25t = - 4,5 t = - 2
Тогда получим координаты точки F:
F= (4,5 + t; - 3 – 0,5t; 2 + t) = (4,5 - 2; - 3 – 0,5 (-2); 2 - 2) =
= (2,5; - 2; 0)
Итак, точка F(2,5; - 2; 0) – точка пересечения с заданной прямой перпендикуляра, опущенного из точки М. Координаты искомой симметричной точки М найдем из формул:
![]()
х М = 2хF – хМ = 2 · 2,5 – 2 = 3
y М = 2yF – yМ = 2 · (- 2) – (-1) = - 3
z М = 2zF – zМ = 2 · 0 – 1 = - 1
Получили точку М (3; - 3; -1) – точка, симметричная точке М относительно заданной прямой.
Ответ: (3; - 3; -1)
Задача 31
Составить
уравнение линии, каждая точка которой
равно удалена от
точки
![]() и от оси абсцисс.
и от оси абсцисс.
Решение
Пусть точка М(х; у) принадлежит искомой линии, а точка В(х; о) – проекция точки М(х; у) на ось Ох.
По условию
![]() .
.

Находим векторы
![]()
![]()
![]()
![]()
![]() =
у
=
у
Возведем в квадрат обе части равенства:
![]() =
у2
=
у2
![]()
![]()
![]() - уравнение искомой линии. Приведем его
к каноническому виду:
- уравнение искомой линии. Приведем его
к каноническому виду:
![]()
Получили уравнение параболы с вершиной в точке (2; 1).
Ответ:
![]()
