Контрольная работа №1(1)
.doc
ВАРИАНТ №3
Контрольная работа №1
Задание 1.
Даны четыре вектора
(а1,
а2, а3),
(b1,
b2, b3),
(c1,
c2, c3) и
(d1,
d2, d3) в некотором базисе. Показать, что
векторы
,
,
образуют базис, и найти координаты
вектора
в этом базисе.
(-2,3,5),
(1,-3,4),
(7,8,-1),
(1,20,1).
Решение.
Базисом в пространстве являются любые три некомпланарных вектора. Условием компланарности трех векторов является равенство их смешанного произведения нулю. Итак, находим
(
,
,
)
=
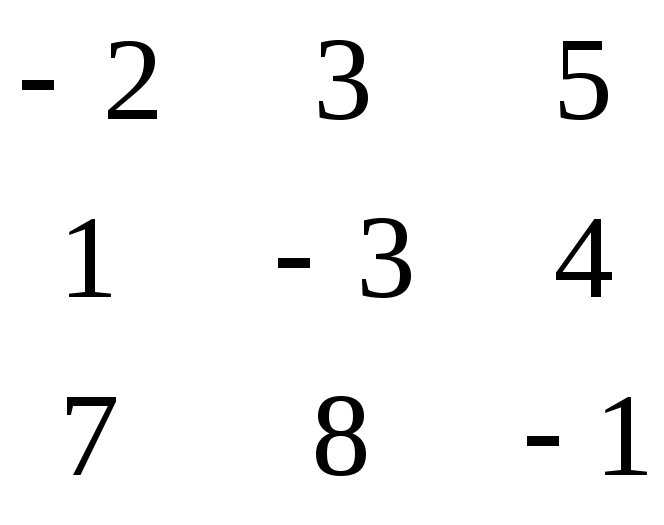= -2
- 3
+ 5
= -2(3-32) - 3(-1 - 28) + +5(8+21) = 58 + 87 +145 =290
Значит, векторы
,
,
некомпланарные и образуют базис.
=
x
+y
+z
Составим систему уравнений
(1)
(2)
(3)
из уравнения (1) выразим x
x=
(3.1)
подставим его значение в уравнение (2) и (3), получаем
20 =
-3y+8z
(4)
1 =
+4y-z
(5)
Решаем уравнение (4)
3y+21z-3-6y+16z=40
5y+35z-5+8y-2z=2
37z-3y=43
13y+33z=7
y=
(6)
Подставим значение y в уравнение (5)
43=37z-
481z-21+99z=580
580z=580
z=1
Значение z подставляем в уравнение (6) находим у
y=
=-2
Значение z и у подставляем в уравнение (3.1) находим х
x=
=2
Отсюда
равно
=
2
-2
+
Ответ:
,
,
образуют базис и
=
2
-2
+
.
Задание 2
1. Даны координаты вершин пирамиды A1A2A3A4. Найти: 1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4; 3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объём пирамиды; 6) уравнения прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнения высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертёж.
A1(3,5,4), A2(5,8,3), A3(1,9,9), A4(6,4,8)
Решение.
1. Находим координаты вектора
=(5-3,8-5,3-4)=(2,3,-1)
и длину ребра
=
=
=
2.
Угол между ребрами A1A2и A1A4вычисляется по
формуле
из
скалярного произведения.
=
(2,3,-1),
=
(6-3,4-5,8-4)=(3,-1,-4)
(
,
)
= (2▪3+3▪(-1)+(-1)▪(-4)) = 6-3+4 = 7
=
=
=
.
Поэтому cosφ=
=
03669
φ = 76°08'
3. Вектор
перпендикулярен
грани A1A2A3
=(1-3,9-5,9-4)=(-2,4,5)
=
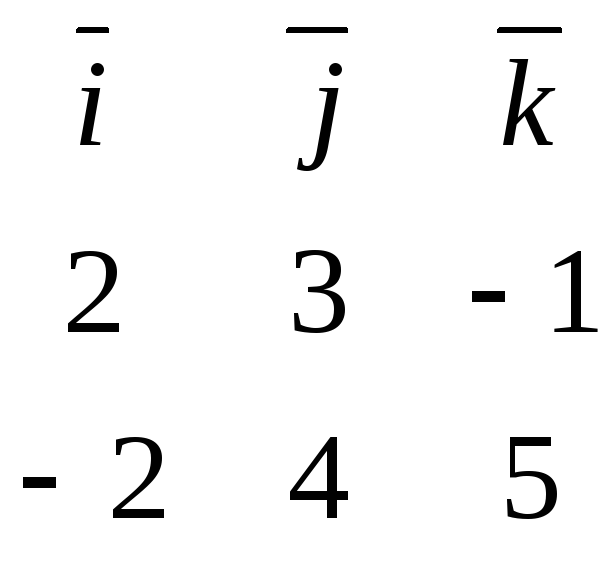= 19
-8
+14
.
cos(
)
= sin
=
(3*19+(-8)*(-1)+(-1)*14) = (57+8-14)= 51
=
=
=
=3
sin
=
=
=
=
=0,401
=
26°27'
4. Площадь грани A1A2A3 находим, используя геометрический смысл векторного произведения
SΔA1A2A3 =
=
=
.
5. Объем пирамиды
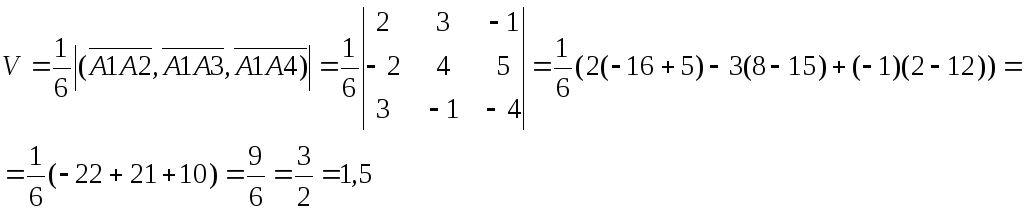
6.
A1(3,8,3)
x0 = 3, y0 = 5, z0 = 4
A2(5,8,3)
x1 = 5, y1 = 8, z1 = 3
В
таком виде уравнения прямой называются
каноническими. Они могут быть записаны
x-2z+11=0
или 3x+2y+5=0
т.е. уравнение прямой как линии пересечения двух плоскостей.
7. Для составления уравнения плоскости воспользуемся формулой (1.6), где - координаты , - координаты , - координаты .
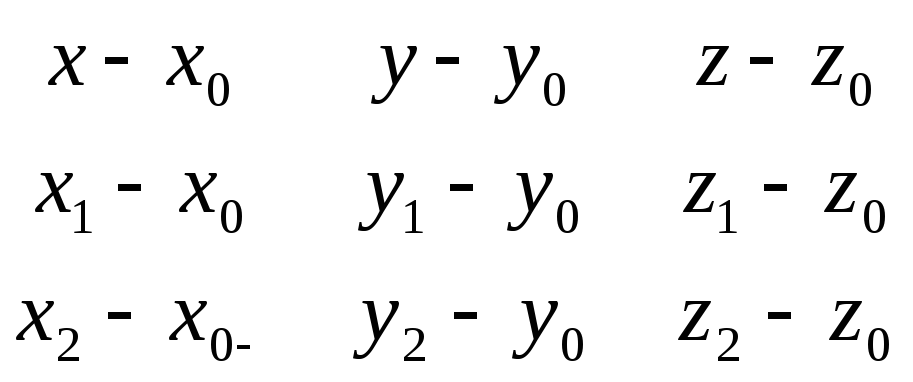= 0
A3 (1,9,9)
x2 = 1, y2 = 9, z2 = 9
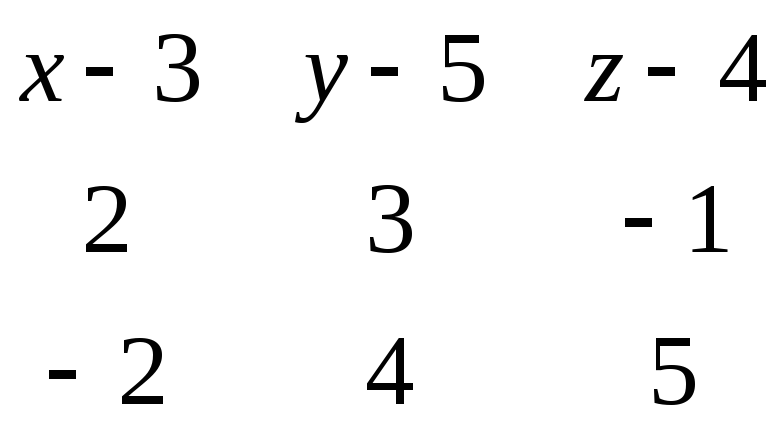= 0
(x-3)(15+4)-(y-5)(10-2)+(z-4)(8+6)=0
19x -8y +14z – 73 = 0
8. Искомые уравнения высоты получим из канонических уравнений прямой , где - точка, лежащая на искомой прямой,; - координаты вектора , параллельного искомой прямой. При этом в качестве точки возьмем точку A4(6,4,8)
x0=6, y0=4,
z0=8 а в качестве
вектора
возьмем
нормальный вектор плоскости
,
т.е.
m=19, n=-8, p=14.
Имеем
.
9. Сделаем чертеж
Задание 3
Найти координаты точки А, симметричной точке A(2,-4) относительно прямой 4x+3y+1=0.
Решение.
B каноническом виде
т.е. направляющий вектор прямой
это вектор ┴ вектору A0A
= (x-x0,y-y0)=(x-2,y+4)
0=(
)=
-3(x-2)+4(y+4)=-3x+6+4y+16=-3x+4y+22=0
(1)
Так как координаты точки середина
отрезка определяется x=
Середина отрезка
Q=
подставляем в ур-ние прямой
2(2+х)-6+
y+1=0
4+2x-6+
y+1=0
2x+
y-1=0
4x+3y-2=0 (2)
С
оставляем
систему (1) и (2)
-3x+4y+22=0
4x+3y-2=0
x=
4▪22+16y+9y-6=0
25y+82=0
y=
x=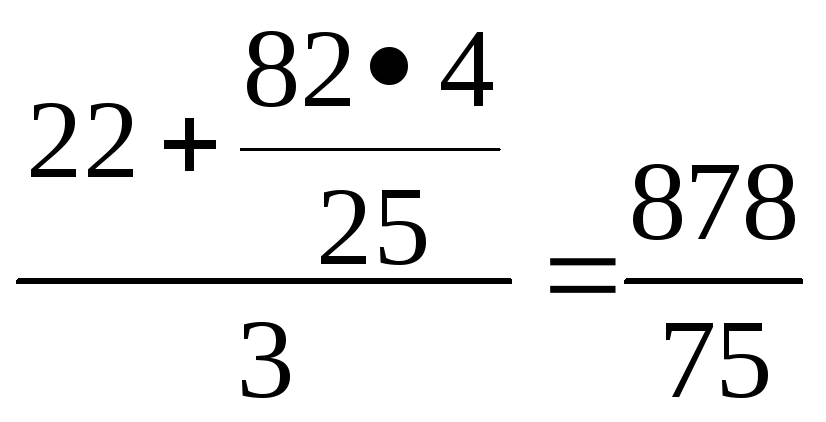
A=
Задание 4
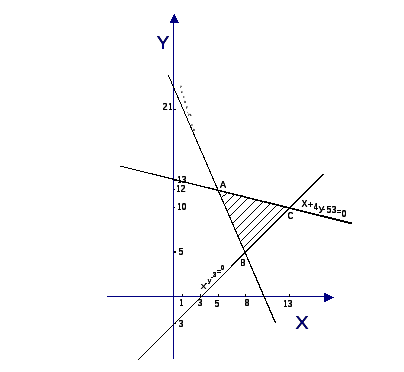
Построить на плоскости область решений системы линейных неравенств.
x
-4y
53
x-y
3
7x+3y
71
Решение.
Построим график :
Н
аходим
т. А пересечения прямых 7x+3y=71
и x+4y=53
7x+3y=71 (1)
x+4y=53 (2)
x=53-4y
подставляем x в ур-ние (1)
7(53-4y)+3y=71
371-28y+3y-71=0
-25y=-300
y=12
находим x
x=53-4▪12=5
x
=5
y=12 A(5,12)
н
аходим
координаты точки B:
7x+3y=71
x-y=3
x=3+y
7(3+y)+3y=71
21+7y+3y=71
10y=50
y=5
x
=3+5=8
x=8
y=5 B(8,5)
н
аходим
координаты точки C:
x+4y=53
x-y=3
x=3+y
3+y+4y=53
5y=50
y=10
x=3+10=13
x
=13
y=10 C(13,10)
Данной системе неравенств удовлетворяют все точки внутри ΔABC и на его границе.
задание 5
Составить уравнение линии, для каждой точки которой отношение расстояния до начала координат к расстоянию до прямой 3x+16=0 равно 0,6.
Решение.
A0(0,0)
Произвольная точка A(x,y),
тогда
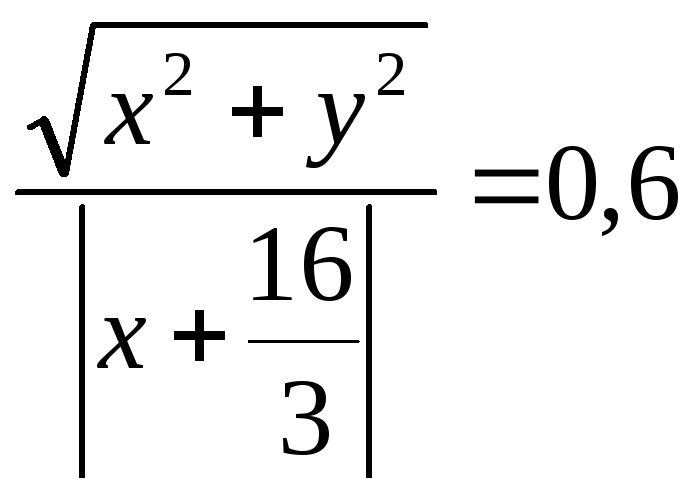
100(x2+y2)=36
100x2+100y2-36x2-384x-1024=0
64x2-384x-1024+100y2
64(x2-6x+9)-1600+100y2=0
64(x-3)2+(10y)2=1600
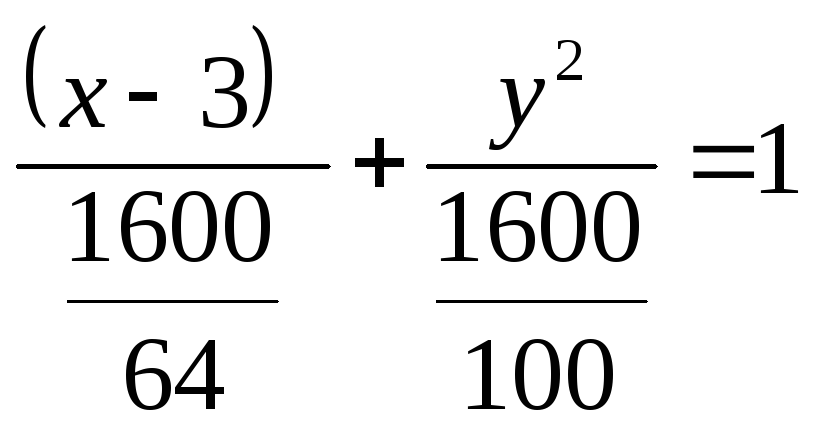
Каноническое ур-ние эллипса с полуосями a=5, b=4 и центром x0=3 y0=0