
BM часть 2. Контрольная работа №5. Вариант №8
.doc
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра программного обеспечения информационных технологий
Факультет НиДО
Специальность ПОИТ
Контрольная работа № 5
по дисциплине «Высшая математика»
Вариант № 8
Выполнил студент: ********
группа ******
Зачетная книжка № ******-**
Электронный адрес ******@****.***
Минск 2011
Задача 218
Дана функция
![]() .
Показать, что
.
Показать, что
![]() .
.
Решение:
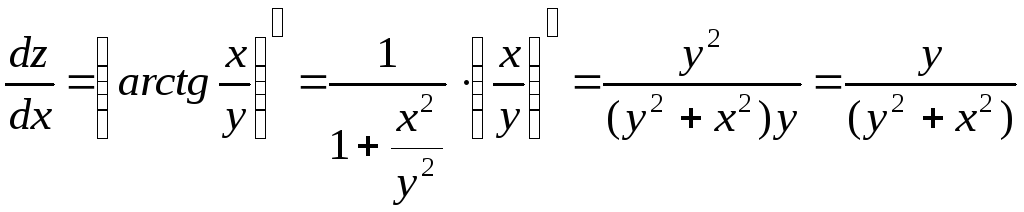
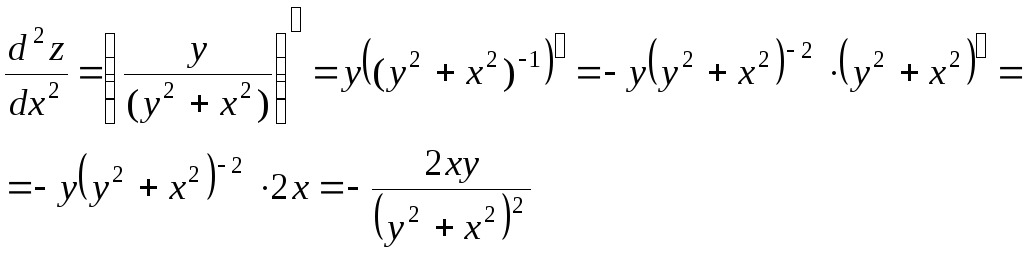
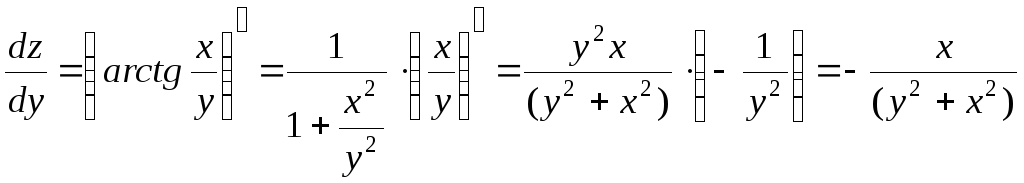
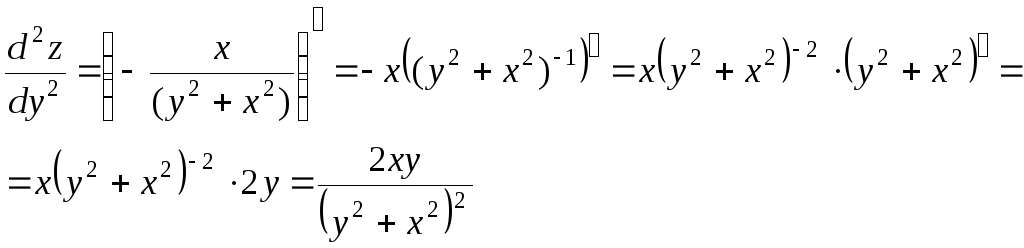
![]()
Задача 228
Дана функция
![]() и две точки
и две точки
![]() и
и
![]() .
Требуется: 1) вычислить значение
.
Требуется: 1) вычислить значение
![]() функции в точке
функции в точке
![]() ;
2) вычислить приближенное значение
;
2) вычислить приближенное значение
![]() функции в точке
функции в точке
![]() исходя из значения
исходя из значения
![]() функции в точке
функции в точке
![]() ,
заменив приращение функции при переходе
от точки
,
заменив приращение функции при переходе
от точки
![]() к точке
к точке
![]() дифференциалом; оценить в процентах
относительную погрешность, возникающую
при замене приращения функции ее
дифференциалом; 3) составить уравнение
касательной плоскости к поверхности
дифференциалом; оценить в процентах
относительную погрешность, возникающую
при замене приращения функции ее
дифференциалом; 3) составить уравнение
касательной плоскости к поверхности
![]() в точке
в точке
![]() .
.
![]() ,
, ![]() ,
, ![]()
Решение:
1)
![]()
2)
![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]()
![]()
![]()
3)
![]()
![]() – уравнение касательной плоскости к
поверхности
– уравнение касательной плоскости к
поверхности
![]() в точке
в точке
![]() .
.
![]() ,
, ![]()
![]() ,
, ![]()
![]()
![]()
Задача 238
Исследовать на экстремум функцию двух переменных.
![]()
Решение:
Для нахождения экстремумов функции воспользуемся свойствами производных:
![]()
![]()
Система для нахождения точек возможных экстремумов:
![]()
![]() – стационарная точка
– стационарная точка
Составим матрицу Гессе:
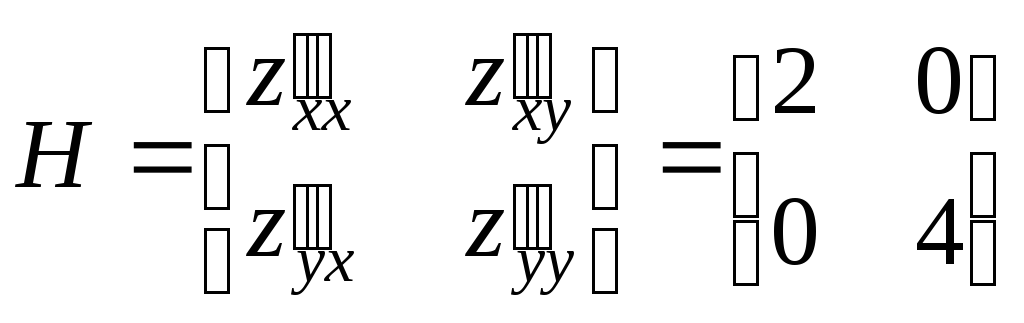
Т.к.
![]() и
и
![]() ,
то
,
то
![]() – точка минимума
– точка минимума
Задача 248
Дана функция
![]() ,
точка
,
точка
![]() и вектор
и вектор
![]() .
Найти: 1)
.
Найти: 1)
![]() в точке
в точке
![]() ;
2) производную в точке
;
2) производную в точке
![]() в направлении вектора
в направлении вектора
![]() .
.
![]() ,
, ![]() ,
, ![]()
Решение:
1)
![]()
![]()
![]()
![]()
![]()
![]()
2)
![]()
![]()
![]()
![]()
![]()
Задача 258
Найти условный экстремум функции при помощи функции Лагранжа.
![]() ,
при
,
при
![]() .
.
Решение:
![]() – функция Лагранжа
– функция Лагранжа
![]()
![]()
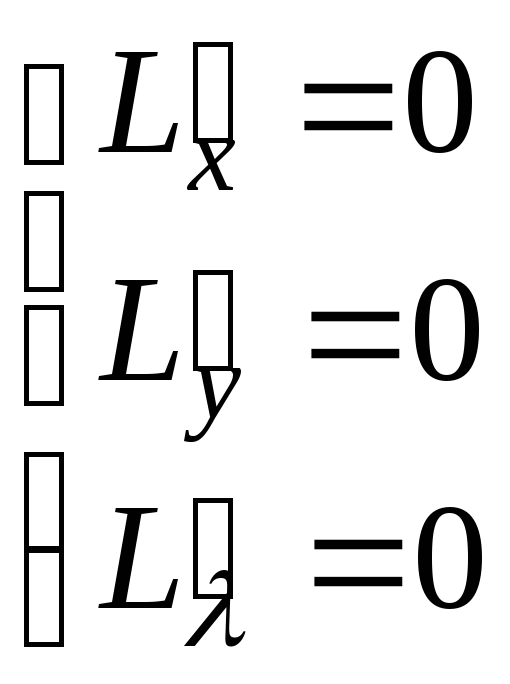
![]()
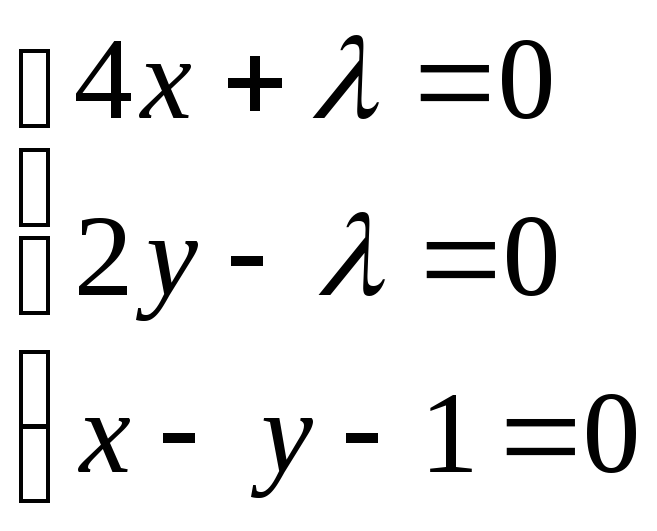
![]()
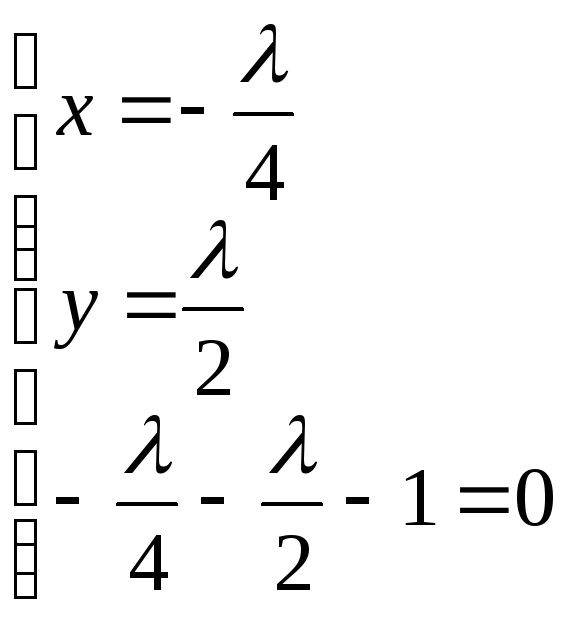
![]()
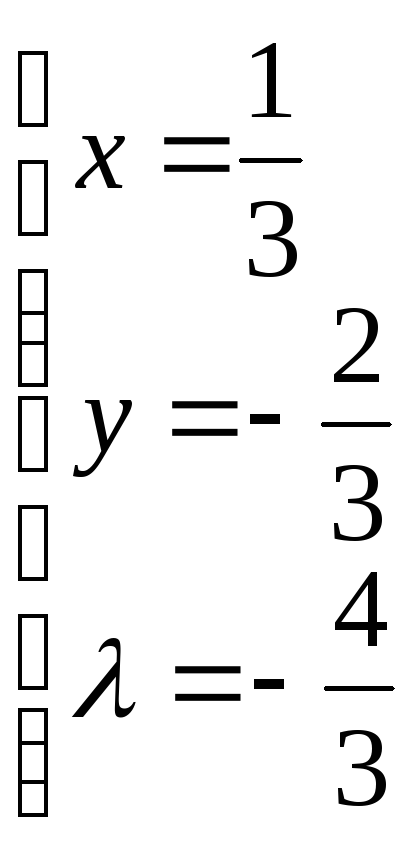
![]() – стационарная точка функции Лагранжа
– стационарная точка функции Лагранжа
![]() – точка возможного условного экстремума
– точка возможного условного экстремума
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Т.к.
![]() ,
то
,
то
![]() и
и
![]()
![]()
![]()
![]() – точка условного минимума
– точка условного минимума
![]() – условный минимум
– условный минимум
