ВМ Контрольна 2 вариант 8

Белорусский государственный университет информатики и радиоэлектроники

Факультет заочного и дистанционного обучения

Контрольная работа №2

по математике

58. Доказать совместность системы линейных уравнений и решить ее двумя способами: методом Гаусса и средствами матричного исчисления.

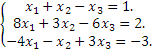
1. Для решения системы методом Гаусса составим расширенную матрицу и приведем ее к ступенчатому виду:

-х₃ = 13 -5х₂+2х₃ = -6 х₁+х₂-х₃ = 1

х₃ = -13 х₂ = = -4 х₁=1-х₂+х₃=-8

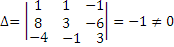2. => воспользуемся формулой Х = А^-1·В

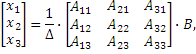
где , а - алгебраические дополнения элементов матрицы А:

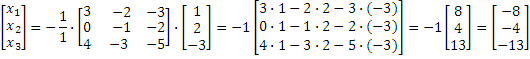
68. Найти размерность и базис пространства решений однородной системы линейных уравнений.

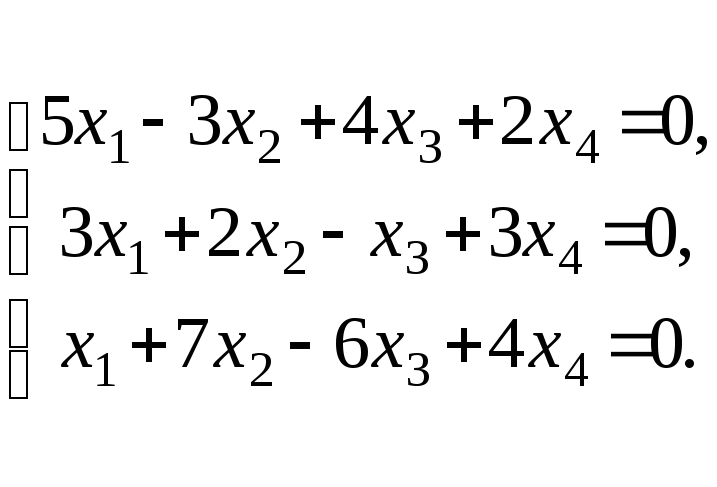
Составим основную матрицу и определим ее ранг:

=> r_A=2

Т.к. r_A=2 меньше количества неизвестных, то система имеет ненулевые решения. Размерность пространства решений этой системы n-r = 2. Преобразованная система, эквивалентная исходной, имеет вид:

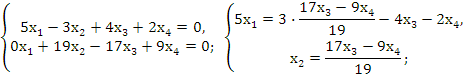
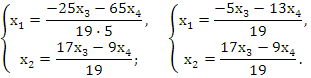
Общее решение в векторном виде:

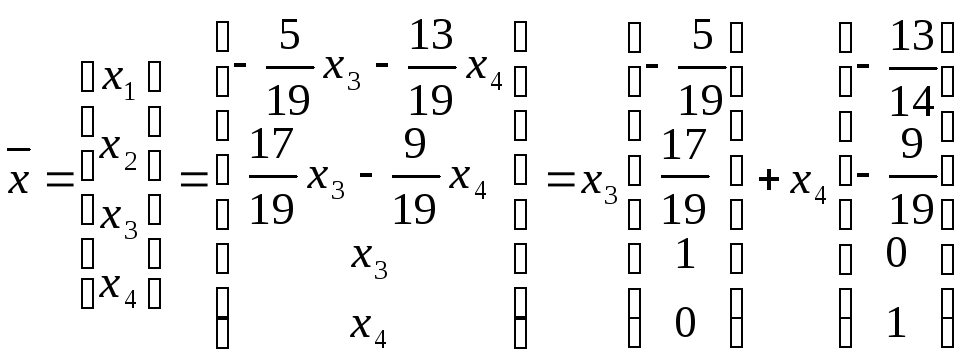
х₃ и х₄ – произвольные числа. Вектор-столбцы 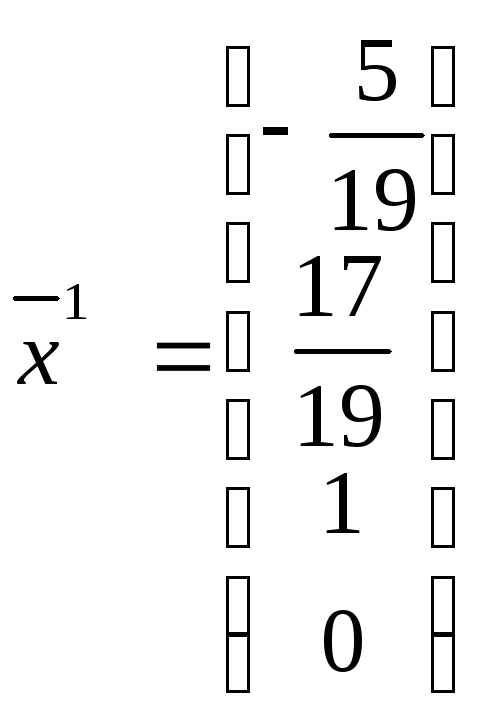и 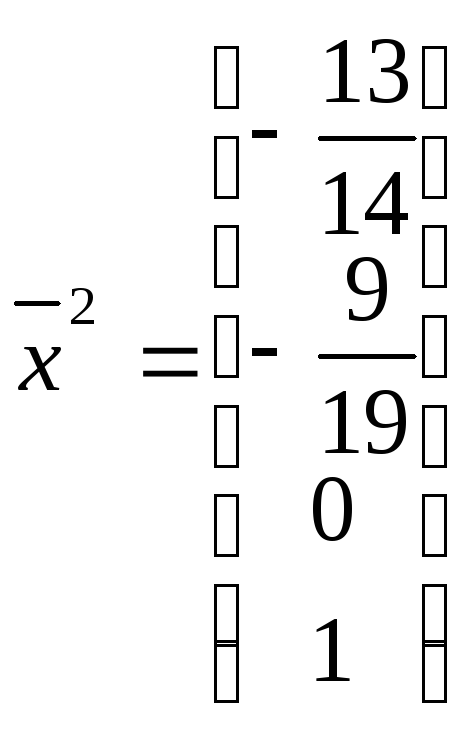образуют базис пространства решений данной системы.

При х₃=С₁ и х₄=С₂, общее решение в векторном виде.

78. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее через

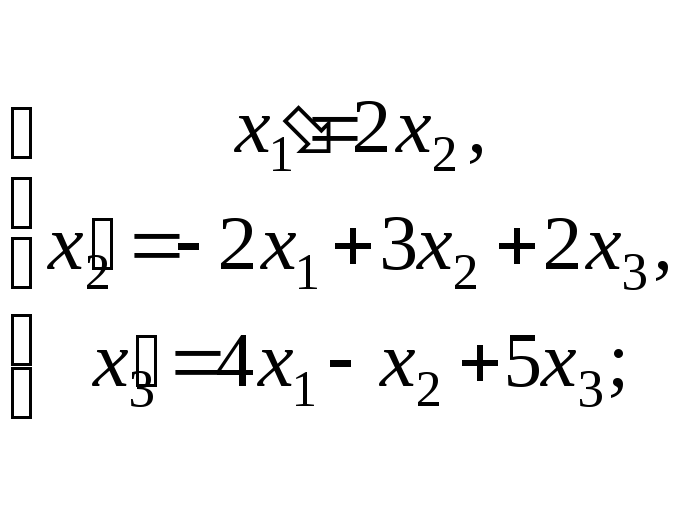
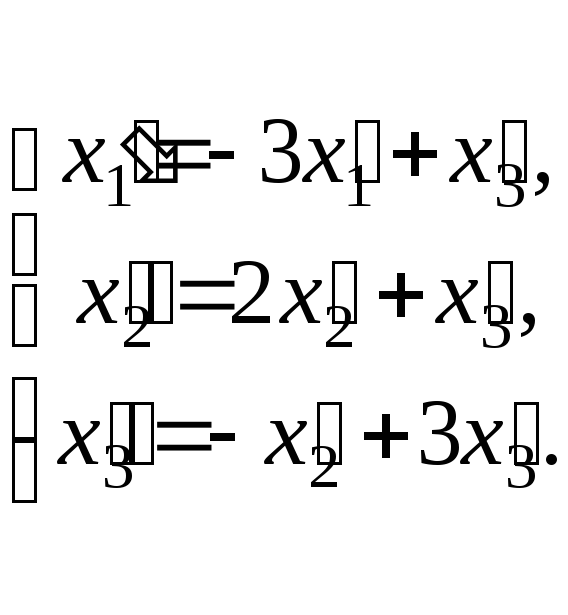
Первое линейное преобразование 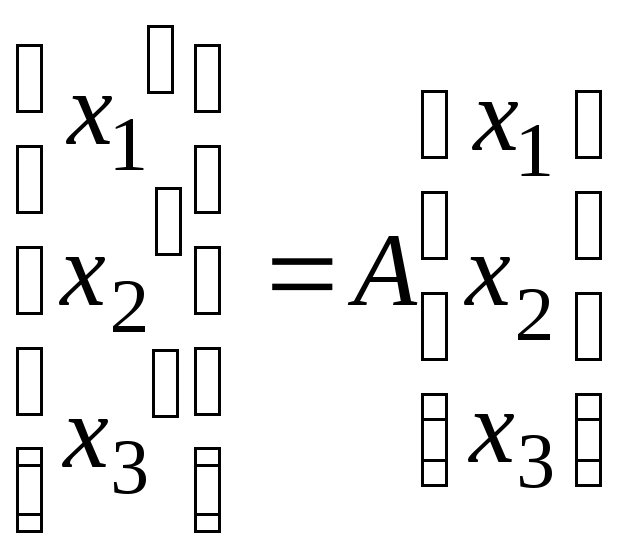имеет матрицу 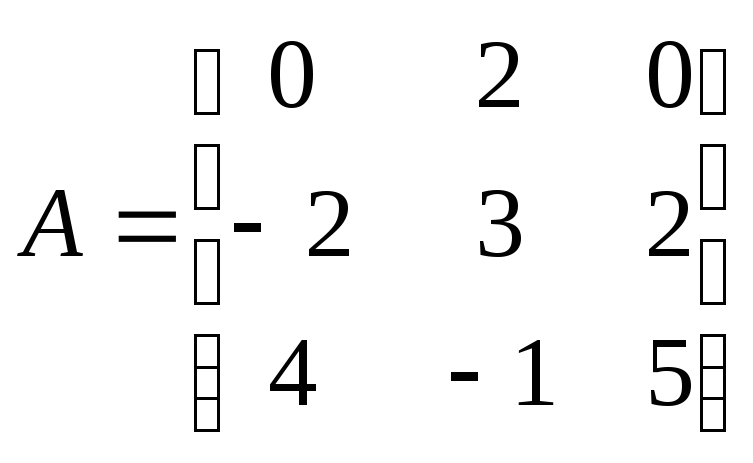, второе 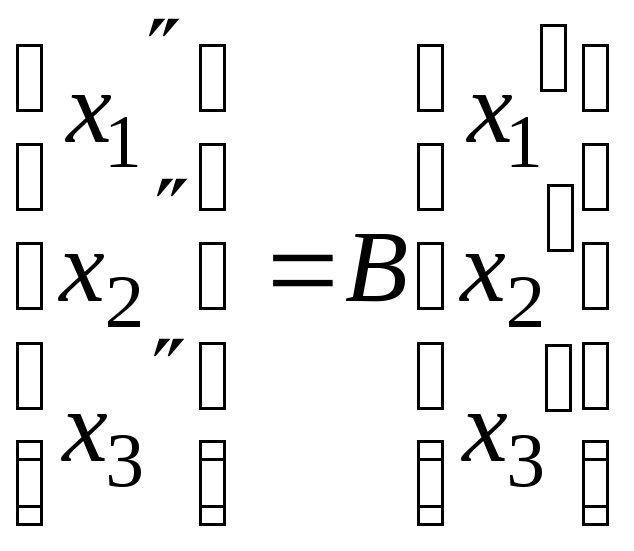имеет матрицу 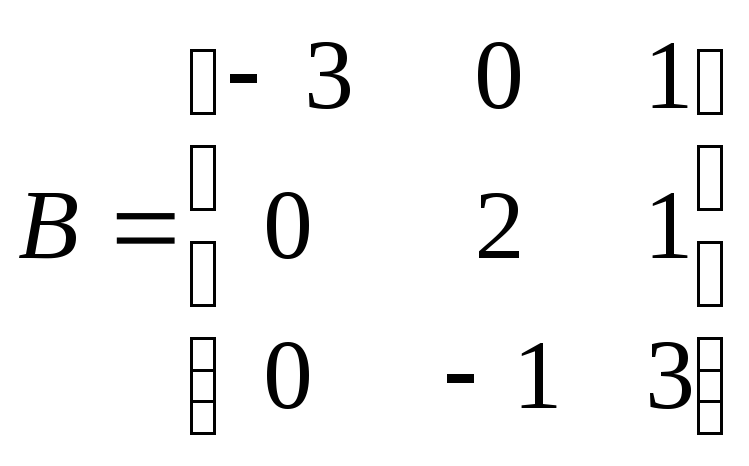. Тогда последовательное выполнение линейных преобразований имеет матрицу , т.е.

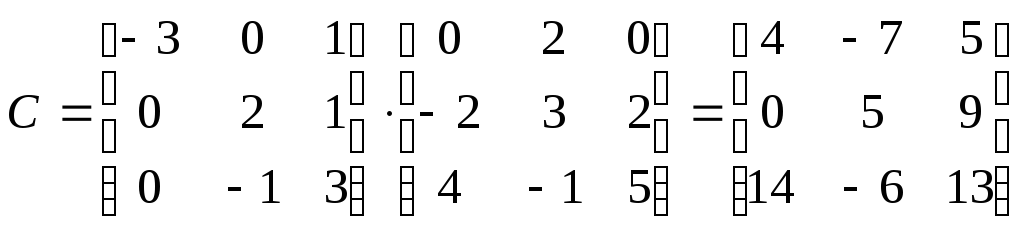
Поэтому искомое линейное преобразование имеет вид

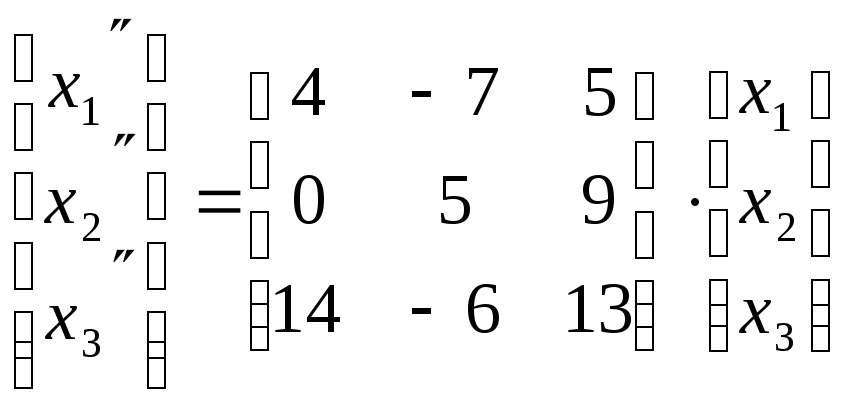
88. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

Составляем характеристическое уравнение матрицы:

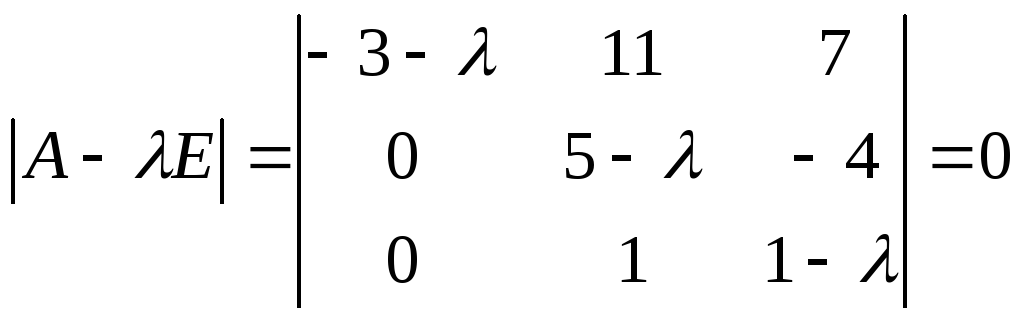
=(-3-λ)(5- λ)(1- λ)-[-4(-3- λ)]= λ³-3 λ²-9 λ+27=0

(λ+3)( λ-3)²=0 => λ₁=3, λ₂=-3

При λ₁=3 система имеет вид:

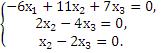
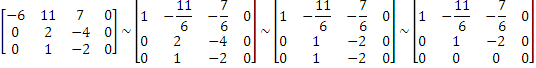
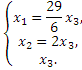
Таким образом, числу λ₁=3 соответствует собственный вектор:

,

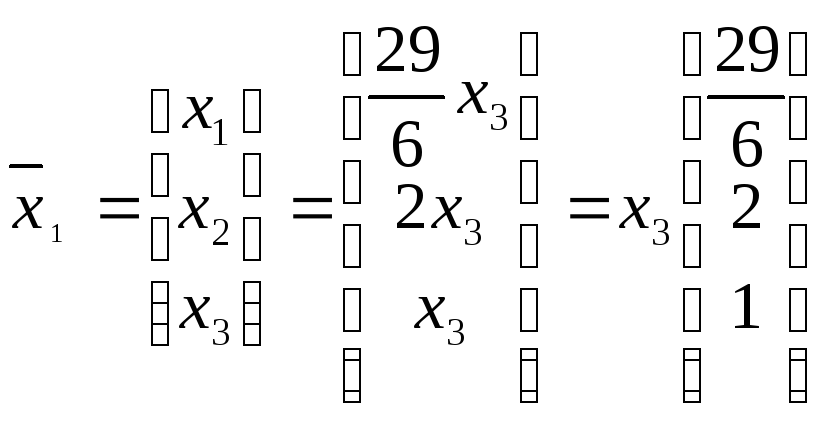где х₃ – произвольное действительное число. В частности при х₃=1 имеем .

При λ₂=-3 система имеет вид:

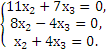
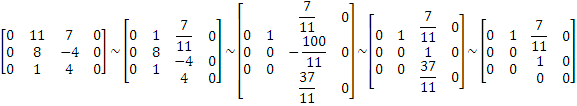
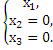
Таким образом, числу λ₂=-3 соответствует собственный вектор:

,

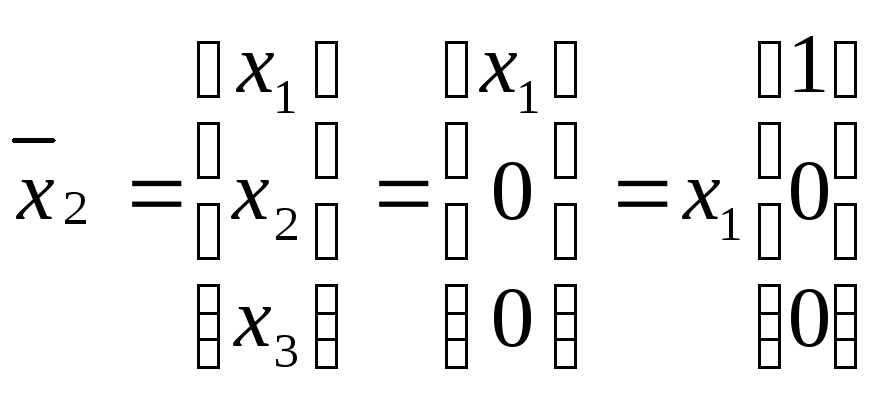где х₁ – произвольное действительное число. В частности при х₁=1 имеем .

98. Привести к каноническому виду уравнение линии второго порядка (1), используя теорию квадратичных форм.

Левая часть уравнения представляет собой квадратичную форму с матрицей . Решаем характеристическое уравнение:

т.е.

(9-λ)(2- λ)-8=0

λ²-11λ+10=0

(λ-10)( λ-1)=0

λ₁=1; λ₂=10

Координаты собственных векторов:

Полагая, что m₁=1; получим n₁=.

Полагая, что m₂=1; получим n₂= .

Собственные векторы:

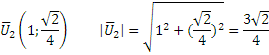
Координаты единичного вектора нового базиса:

Составляем матрицу перехода от старого базиса к новому, в которой координаты нормированных собственных векторов записаны по столбцам:

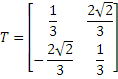
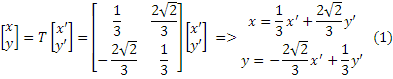
Подставив полученные выражения в исходное уравнение получаем:

х’²+10y’²=20

Последнее уравнение есть уравнение эллипса.