
BM Контрольная работа №2. Вариант №8
.doc
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра программного обеспечения информационных технологий
Факультет НиДО
Специальность ПОИТ
Контрольная работа № 2
по дисциплине «Высшая математика»
Вариант № 8
Выполнил студент: ******
группа ******
Зачетная книжка № ******-28
Электронный адрес ******@****.***
Минск 2010
Задача 58
Доказать совместность данной системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.

Решение:
Система, имеющая хотя бы одно решение, называется совместной.
1) методом Гаусса
Необходимым и достаточным условием совместности системы линейных уравнений является Критерий Кронекера–Капелли. Для того чтобы линейная система была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы.
 – основная матрица
– основная матрица
Рангом системы строк (столбцов) матрицы А называется максимальное число линейно независимых строк(столбцов). Несколько строк (столбцов) называются линейно-независимыми, если ни одна из них не выражается линейно через другие.
![]()
 – расширенная матрица
– расширенная матрица
Для нахождения ранга расширенной матрицы с помощью элементарных преобразований, необходимо привести ее к треугольному или трапециевидному виду.

Отсюда видно, что ранг расширенной
матрицы равен рангу основной матрицы
системы и равен количеству неизвестных
![]() :
:
![]() система
совместна и имеет единственное решение
система
совместна и имеет единственное решение
Система сводится к эквивалентной системе линейных уравнений



Ответ:
![]() ,
,
![]() ,
,
![]() .
.
2) средствами матричного исчисления

Следовательно, система совместна и для матрицы коэффициентов существует обратная матрица.
Решение системы линейных уравнений
матричным методом находится по формуле:
![]() ,
где
,
где
![]() – матрица-столбец неизвестных,
– матрица-столбец неизвестных,
![]() – обратная матрица, основной матрицы
системы,
– обратная матрица, основной матрицы
системы,
![]() – матрица-столбец правой части системы
уравнений.
– матрица-столбец правой части системы
уравнений.



Необходимо найти обратную матрицу
![]() по формуле:
по формуле:
 ,
где
,
где
![]() –
алгебраическое дополнение, Mij
– минор, получается путем удаления i–ой
строки и j–ого столбца, det A – детерминант
матрицы A (
–
алгебраическое дополнение, Mij
– минор, получается путем удаления i–ой
строки и j–ого столбца, det A – детерминант
матрицы A (![]() ).
).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Необходимо проверить правильность
вычисления обратной матрицы, исходя из
формулы:
![]() ,
где
,
где
![]() – единичная матрица, матрица у которой
элементы на главной диагонали равны
единице, а остальные – нулю.
– единичная матрица, матрица у которой
элементы на главной диагонали равны
единице, а остальные – нулю.


![]()
![]()
![]()
Ответ:
![]() ,
,
![]() ,
,
![]() .
.
Задача 68
Найти размерность и базис пространства решений однородной системы линейных уравнений.

Решение:
Необходимо найти ранг основной матрицы системы с помощью элементарных преобразований:

Так как ранг системы меньше числа
неизвестных, то система имеет ненулевые
решения. Размерность пространства
решений этой системы:
![]() ,
где
,
где
![]() – количество неизвестных системы.
– количество неизвестных системы.
 – преобразованная система
– преобразованная система

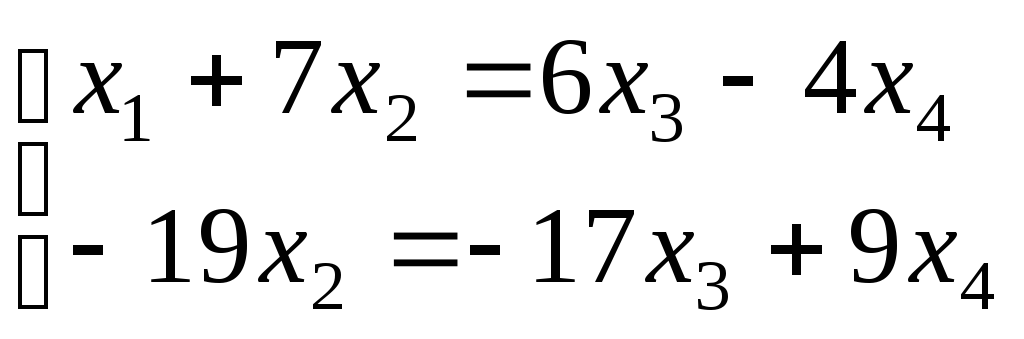


Эти формулы дают общее решение. В векторном виде его можно записать следующим образом:
 ,
,
где
![]() и
и
![]() – произвольные числа.
– произвольные числа.
Вектор-столбцы:
 и
и
 образуют базис пространства решений
данной системы.
образуют базис пространства решений
данной системы.
При
![]() и
и
![]() общее решение в векторном виде
общее решение в векторном виде
![]()
Задача 78
Даны два линейных преобразования.
Средствами матричного исчисления найти
преобразование, выражающее
![]() через
через
![]() .
.

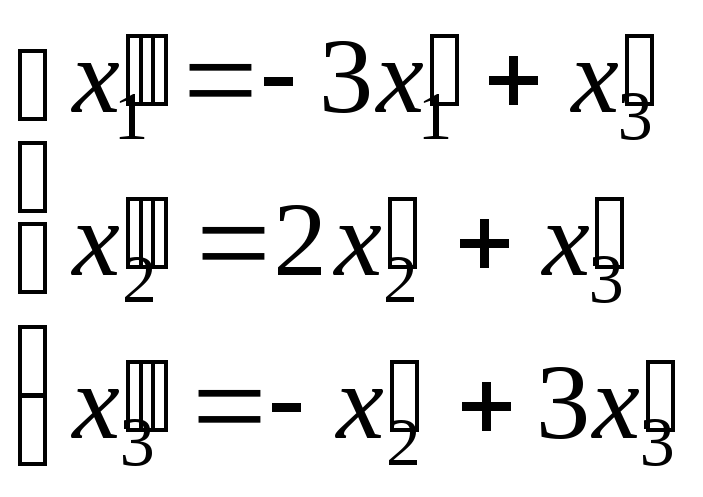
Решение:
Первое линейное преобразование:
 ,
где
,
где

Второе линейное преобразование:
 ,
где
,
где


Ответ:

Задача 88
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

Решение:
Необходимо составить характеристическое уравнение матрицы:

![]()
![]()
![]()
![]()
Корни этого уравнения – собственные значения матрицы:
![]() ,
,
![]()
Необходимо найти собственные векторы:

При
![]() система имеет вид:
система имеет вид:


 ,
где
,
где
![]() – любое число. При
– любое число. При
![]()
![]()
При
![]() система имеет вид:
система имеет вид:


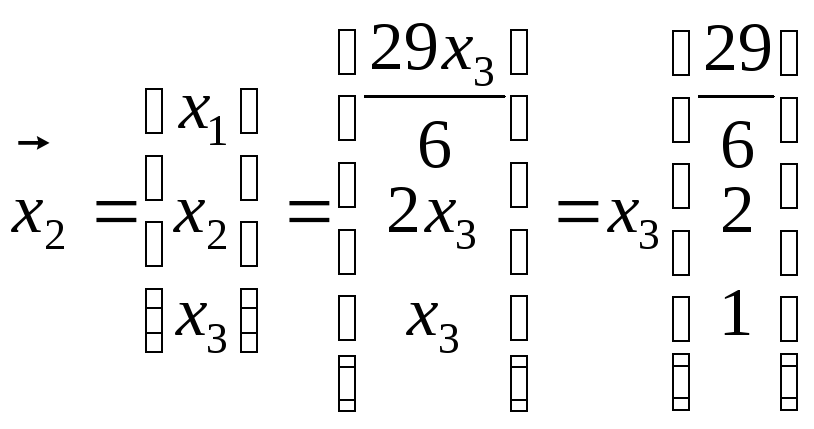 ,
где
,
где
![]() – любое число не равное нулю. При
– любое число не равное нулю. При
![]()
![]()
Задача 98
Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм.
![]()
Решение:
Левая часть уравнения
![]() представляет собой квадратичную форму
с матрицей
представляет собой квадратичную форму
с матрицей
![]()
Необходимо составить и решить характеристическое уравнение матрицы:
![]()
![]()
![]()
![]()
![]() ,
,
![]()
Необходимо найти собственные векторы из системы уравнений

При
![]() система имеет вид:
система имеет вид:

Полагая, что
![]() ,
получаем
,
получаем
![]()
Собственный вектор –
![]()
![]()
При
![]() система имеет вид:
система имеет вид:

Полагая, что
![]() ,
получаем
,
получаем
![]()
Собственный вектор –
![]()
![]()
Координаты единичного вектора нового базиса:
![]() ;
;
![]()
![]()
![]()
Необходимо составить матрицу перехода от старого базиса к новому, в которой координаты нормированных собственных векторов записаны по столбцам:


Необходимо подставить полученные выражения в исходное уравнение:



![]()
 – уравнение эллипса.
– уравнение эллипса.
