
Высшая математика 1курс 2семестр(Вариант №4)
.doc
124.
Найти производную
![]() данных функций:
данных функций:
а)
![]()
![]()
б)
![]()
![]()
в)
![]()
![]()
г)
![]()
Прологарифмируем
обе части уравнения
![]() и преобразуем равенство
и преобразуем равенство
![]() Прологарифмируем обе части равенства
Прологарифмируем обе части равенства
![]()
![]()
д)![]() Дифференцируем обе части равенства,
учитывая, что у
есть функция от х,
получим
Дифференцируем обе части равенства,
учитывая, что у
есть функция от х,
получим
![]() или
или
![]()
![]()
![]()
134. Найти
![]() и
и
![]()
a)![]()

![]()
б)
![]()
![]()
Получаем
![]()

Получаем
![]()
144. Из полосы жести шириной 11 см требуется сделать открытый сверху желоб, поперечное сечение которого имеет форму равнобедренной трапеции. Дно желоба должно иметь ширину 7 см. Какова должна быть ширина желоба наверху, чтобы он вмещал наибольшее количество воды?
b a h x
![]()
По условию а=7 см, боковые стороны трапеции (11-7)/2=2 см.
Высоту находим по
теореме Пифагора
![]() ,
b=
7+2х, тогда
,
b=
7+2х, тогда
S(х)=![]() ,
х
,
х![]()
Найдем производную функции
S´(х)=![]()
Для нахождения точек экстремума решим уравнение S´(х)=0
![]()
![]()
х1=-4
х2=0,5,
т.к. по условию х![]() ,
то корнем является только х2=0,5
,
то корнем является только х2=0,5
S(х)

+
-
0,5
S(х)

х=0,5 точка максимума функции, значит. наибольшую площадь трапеции получаем (и наибольшее количество воды в желобе при х=0,5, ширина желоба на верху b=7+2x=8 см
Ответ: 8 см.
154. Провести полное исследование функции и построить ее график
![]()
1) Область определения
D(y)=![]()
2) Т.к. область определения не симметрична относительно начала координат, то функция не является ни четной, ни нечетной.
3) Точки пресечения с осями координат
с Ох : у=0 х=0,5 т.(0,5; 0)
с Оу: х=0 у= -1 т. (0;-1)
4) Асимптоты
Т.к. точка разрыва 1, то находим пределы
![]()
прямая х=1 вертикальная асимптота
 у=0 горизонтальная
асимптота
у=0 горизонтальная
асимптота
Проверим, существует ли наклонная асимптота
 ,
т.е. наклонной асимптоты нет.
,
т.е. наклонной асимптоты нет.
5)Промежутки возрастания, убывания, точки экстремума
![]()
у![]()

-
-
+
0
1
у



точка разрыва min
Функция возрастает на промежутке (0;1) и убывает на промежутках (-∞;0) и (1;+ ∞), х=0 точка минимума у(0)= -1, х=1 точка разрыва функции
6) Выпуклость, вогнутость функции

![]() =0
при х=-0,5, т
=0
при х=-0,5, т
y''
у
+
+
-



1
-0,5
Функция вогнута на промежутках (-0,5;1) и (1; +∞) и выпукла на промежутке (-∞;-0,5)
По результатам исследования функции строим график.


164. Дана функция
![]() .
Показать, что
.
Показать, что
![]()
Найдем
![]()
![]()
![]()
![]()
![]() , что и требовалось
показать.
, что и требовалось
показать.
174. Даны функции
![]() и две точки А(1,3) и В(0,95;2,94). Требуется: 1)
вычислить значение z1
функции в точке В; 2) вычислить приближенное
значение z1
функции в точке В, исходя из значений
z0
функции в точке А, заменив приращение
функции при переходе от точки А к точке
В дифференциалом, и оценить в процентах
относительную погрешность, возникающую
при замене приращения функции её
дифференциалом; 3) составить уравнение
касательной плоскости к поверхности
z=f(x,y)
в точке С(х0,у0,z0).
и две точки А(1,3) и В(0,95;2,94). Требуется: 1)
вычислить значение z1
функции в точке В; 2) вычислить приближенное
значение z1
функции в точке В, исходя из значений
z0
функции в точке А, заменив приращение
функции при переходе от точки А к точке
В дифференциалом, и оценить в процентах
относительную погрешность, возникающую
при замене приращения функции её
дифференциалом; 3) составить уравнение
касательной плоскости к поверхности
z=f(x,y)
в точке С(х0,у0,z0).
1)
![]()
2) Будем рассматривать
z(B)
как частное
значение функции
![]() при x
= 0.95 = x1,
у = 2.94 = у1.
За x0
принимаем число 1, за у0
–число 3.
при x
= 0.95 = x1,
у = 2.94 = у1.
За x0
принимаем число 1, за у0
–число 3.
Тогда z(x0,y0)
=
![]() ;
;
Переведём dx в радианы dx = x1 – x0 = 0,95-1=-0,05,
dy = y1 –y0 = 2,94-3= -0,06

Тогда получим:
![]() z(x0,y0)
+
z(x0,y0)
+![]() (x0,y0)dx+
(x0,y0)dx+![]() (x0,y0)dy=-4-10*0.05+4*0.06=-1.26
(x0,y0)dy=-4-10*0.05+4*0.06=-1.26
Оценим погрешность:
![]() %
%
3) Составим уравнение
касательной плоскости к поверхности
z=f(x,y)
в точке С(1,3,-1). Искомое уравнение имеет
вид:
![]() .
.

![]()
184. Найти неопределенные интегралы (в случаях «а» и «б» проверить дифференцированием) :
а)

Проверим результат дифференцированием:

б)

Проверим результат дифференцированием:

в)
![]()
Разобьём дробь на множители:

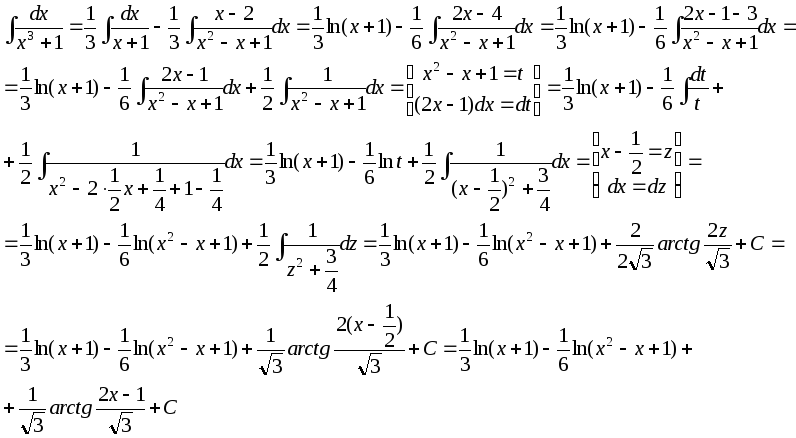
г)
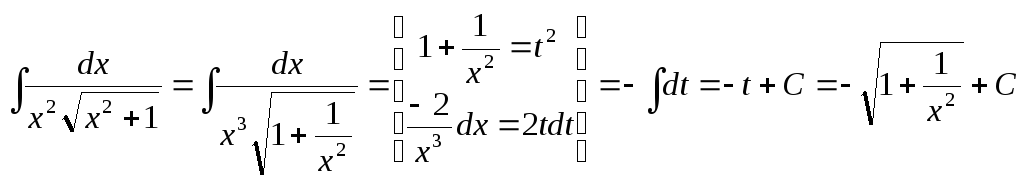
д)


194. Вычислить определённый интеграл:

204. Вычислить несобственный интеграл или доказать его расходимость:

Интеграл расходится.
214. Вычислить
площадь фигуры, ограниченной кривой
![]() .
.
Сделаем чертёж


Контрольная работа
По высшей математике
Вариант 4
Студента ФЗО
Специальность: “Проектирование и производство
радиоэлектронных средств”
Группа: 900201
______________________
Обратный адрес:
____________________________
г. Минск
2009
