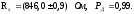Задача №52.
Напряжение сигнала неизвестной формы измерялось тремя вольтметрами, вольтметры имеют открытые входы, шкалы их проградуированы в средних квадратических значениях синусоидального напряжения, детекторы, соответственно, пиковый, среднего квадратического и средневыпрямленного значений. Определить коэффициенты амплитуды и формы, если показания вольтметров с детекторами: пикового значения U1=72 мВ, среднеквадратического значения U2=58 мВ и средневыпрямленного значения – U3=49 мВ.
Решение:
Пиковое значение напряжения можно определить по показанию вольтметра с пиковым детектором, учитывая градуировочный коэффициент:

Среднеквадратическое значение напряжения находим по показанию вольтметра с детектором среднеквадратичного значения (градуировочный коэффициент =1, т. к. тип детектора и шкалы совпадают):

Средневыпрямленное значение напряжения находим, зная показания вольтметра с детектором средневыпрямленного значения и учитывая, что шкала его отградуирована в среднеквадратических значениях синусоидального напряжения:

Определяем искомые значения коэффициентов амплитуды и формы измеряемого напряжения:
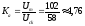

Задача №64.
Определить относительную и абсолютную погрешность измерения периода Тх универсальным цифровым частотомером, если период счетных импульсов Т0, нестабильность частоты кварцевого генератора о.
Значения
Тх=285
мс, То=1,0
мкс, о
=
 .
.
Решение:
Относительная погрешность измерения периода:

N − число подсчитанных импульсов.
Относительная погрешность измерения периода в %:

Абсолютная погрешность измерения периода:

Задача №74.
По приведенной на рисунке в масштабе 1:1 осциллограмме необходимо определить параметры сигналов, указанных в условии задачи.
Значения коэффициентов отклонения Кв=0,5 мВ/дел и развертки Кр=0,1 мкс/дел .
Определить период и длительность фронта импульса.
Решение:

Период сигнала и длительность фронта импульса измеряется между отсчетными точками на значении 0,1 и 0,9 амплитуды наблюдаемого изображения [2].
Период сигнала:

Длительность фронта импульса:
 мкс
мкс
Задача №83.
Необходимо
по типу измеряемого элемента выбрать
схему моста, записать для нее условие
равновесия, получить из него выражения
для Сх,
Rх,
tg или Lx,
Rx,
Q
и определить их. При этом измеряемый
элемент заменить соответствующей
эквивалентной схемой, трансформировав
при необходимости схему моста. На
окончательной схеме показать в виде
переменных элементы (резисторы,
конденсаторы и т.д.), которыми его следует
уравновешивать, чтобы обеспечить прямой
отсчет заданных в условии величин.
Частота питающего напряжения 1 кГц.
Определить абсолютные погрешности
однократного измерения Сх,
Rх,
tg
или Lx,
Rx,
Q
и определить их. При этом измеряемый
элемент заменить соответствующей
эквивалентной схемой, трансформировав
при необходимости схему моста. На
окончательной схеме показать в виде
переменных элементы (резисторы,
конденсаторы и т.д.), которыми его следует
уравновешивать, чтобы обеспечить прямой
отсчет заданных в условии величин.
Частота питающего напряжения 1 кГц.
Определить абсолютные погрешности
однократного измерения Сх,
Rх,
tg или Lx,
Rx,
Q
из-за неидеальности образцовых мер
R2=1100
Ом, R3=1
кОм, R4=16
кОм, C3=82
нФ, если средние квадратические отклонения
случайных погрешностей этих мер R2=0,8
Ом, R3=0,6
Ом, R4=2,6
Ом, C3=0,08
нФ. Значение доверительной вероятности
принять Рд=
0,99.
или Lx,
Rx,
Q
из-за неидеальности образцовых мер
R2=1100
Ом, R3=1
кОм, R4=16
кОм, C3=82
нФ, если средние квадратические отклонения
случайных погрешностей этих мер R2=0,8
Ом, R3=0,6
Ом, R4=2,6
Ом, C3=0,08
нФ. Значение доверительной вероятности
принять Рд=
0,99.

Конденсатор с большими потерями. Прямой отсчет Сх и Rх.
Решение:
Параллельная схема замещения соответствует большим потерям в конденсаторе.

Условие равновесия моста запишется в виде

Преобразовав его и отдельно приравняв действительные и мнимые части, получим выражения для Rx, Cx.

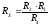


Частные случайные погрешности косвенного измерения:






Оценка среднего квадратичного отклонения результата косвенного измерения:
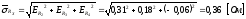

Коэффициент
Стьюдента t
для однократных измерений и заданной
доверительной вероятности РД=0,99
равен
 [2].
[2].
Определим доверительные границы случайной погрешности результата косвенного измерения:


Запишем результат измерения: