«Специальные математические методы и функции»

Вариант 24

1. а.

𝑝	𝑞	𝑟
И	И	И	И
И	И	Л	Л
И	Л	И	И
И	Л	Л	И
Л	И	И	Л
Л	И	Л	Л
Л	Л	И	И
Л	Л	Л	Л

В дизъюнктивной нормальной форме:

1. б. Система множеств {x₁, x₂, …, x_n} наз. разбиением множества А, если она удовлетворяет след. условиям:

1) Любое множество X{x₁, x₂, …, x_n} явл. помножеством мн-ва А.

2) Любые два мн-ва X_i, X_j{x₁, x₂, …, x_n}явл. непересекающимися.

3) Объединение всех мн-в, входящих в разбиение, дает мн-во А.

Задано мн-во 𝐴 = {1, 2, 3, 4, 5, 6, 7}:

а) {{1, 2}, {3, 4, 5}, {6, 7}} - эта совокупность элементов составляет разбиение мн-ва А, т.к. удовлетворяет всем условиям, приведенным выше.

б) {{1, 5}, {3, 4, 5}, {2, 6, 7}} – эта совокупность элементов не явл. разбиением А, т.к. не удовлетворяет условию непересекаемости.

2. а.

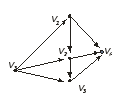Ориентированные пути графа (с указанием длины пути):

v₁v₂(1), v₁v₄(1), v₁v₂v₃(2), v₁v₂v₄(2), v₁v₂v₃v₄(3), v₂v₃(1), v₂v₄(1), v₂v₃v₄(2), v₃v₄(1), v₅v₁(1), v₅v₃(1), v₅v₃v₄(2), v₅v₂(1), v₅ v₁v₂(2), v₅v1v4(2), v₅ v₁v₂v₃(3), v₅ v₁v₂v₄(3), v₅ v₁v₂v₃v₄(4), v₅ v₂v₃(2), v₅ v₂v₄(2), v₅v₂v₃v₄(3).

Для заданного графа невозможно построить цикл.

2. б.

Идея алгоритма Уоршелла состоит в расширении множества промежуточных вершин по следующему правилу: на каждом шаге в рассмотрение добавляется одна новая вершина, после чего достижимости вершин пересчитываются “через нее”. Если w - промежуточная вершина, то достижимость вершины v из вершины u через w пересчитывается по правилу: D[u;v] = D[u;v] ИЛИ (D[u;w] И D[w;v]). Таким образом, получаем матрицу достижимости:

Пути ориентированного графа: v₁v₂v₃v₁, v₁v₂, v₁v₂v₃, v₁v₂v₃v₄, v₂v₃v₁, v₂v₃v₁v₂, v₂v₃, v₂v₃v₄, v₃v₁, v₃v₁v₂, v₃v₁v₂v₃, v₃v₄, v₅v₁, v₅v₁v₂, v₅v₃, v₅v₃v₄.

3. 𝐴 = , 𝐵 =

U = ∨ =

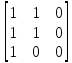𝐼 = ∧ =

= =

4. 𝐺𝐹(4) = GF(2²) ⇒ p = 2, q = 4 (p – хар-ка поля, q – кол-во эл-тов в поле)

2𝑥 +

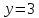
𝑥 + 2𝑦 = 3

y = 1, x = 1.

5. , .

α³ = α² + 1.

α⁰ = 1;

α¹ = α;

α² = α²;

α³ = α² + 1;

α⁴ = α³ + α = α² + α + 1;

α⁵ = α³ + α² + α = α + 1;

α⁶ = α² + α;

α⁷ = α³ + α² = 1;

Минимальный многочлен элемента β поля GF(q^m) определяется по формуле:

Найдем l: условие выполняется при l = 3: α⁴⁸ = α⁶.

Найдем минимальный многочлен элемента α⁶: . Проделав преобразования, получим: M⁶(x) = x³ + x + 1.

6. a. Линейный групповой код с повторением с параметрами [𝑛; 1; 𝑛], 𝑛 = 6.

Длина кодового слова n = 6, кол-во информационных символов k = 1, кодовое расстояние d_min = 6, кол-во проверочных символов r = n – k = 5.

Порождающая матрица:

Проверочная матрица:

6. б. Минимальное расстояние Хэмминга (кодовое расстояние) кода, порождаемого матрицей Адамара d_min = 2.

7. а. Таблица смежных классов:

0000	0011	0101	0110
1000	1011	1101	1110
0100	0111	0001	0010
1100	1111	1001	1010

Для кода Адамара: 0 = 1, 1 = -1.

Получено сообщение , т.е. 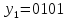- это разрешенная кодовая комбинация, т.е. ошибок нет.

Получено сообщение , т.е. - ошибка произошла в первом разряде, кодовое слово без ошибки: (1 -1 -1 1).

7. б.

- ошибок нет. – есть однократная ошибка.

Т.к. кодовое расстояние для данного кода d_min = 2, то по синдрому можно определить только наличие или отсутствие однократной ошибки (t_o + 1 ≤ d_min, 2t_и + 1 ≤ d_min).

8.

символ	а	б	с	д	е	и	к	р	т
частота	7	12	3	2	9	4	5	8	1

, , , ,

, , ,

, , .

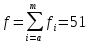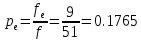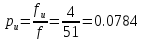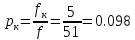б	0,2353	0,2353	0,2353	0,2353	0,2549*	0,3333*	0,4118*	0,5882*	1*
е	0,1765	0,1765	0,1765	0,1765	0,2353	0,2549	0,3333	0,4118
р	0,1569	0,1569	0,1569	0,1764*	0,1765	0,2353	0,2549
а	0,1373	0,1373	0,1373	0,1569	0,1764	0,1765
к	0,098	0,098	0,1176*	0,1373	0,1569
и	0,0784	0,0784	0,098	0,1176
с	0,0588	0,0588	0,0784
д	0,0392	0,0588*
т	0,0196

8. б. Код Хаффмана:

Символ	а	б	с	д	е	и	к	р	т
Вероятность	0,1373	0,2353	0,0588	0,0392	0,1765	0,0784	0,098	0,1569	0,0196
Код	101	01	1001	10001	00	1110	1111	110	10000

9. Даны последовательности длин L = 4 и M = 3, соответственно. Апериодическая (линейная) взаимная корреляция определяется по формуле:

. В матричном виде:

10.

Алгоритм Горнера:

Произвольный полином степени N: . Представим полином p(z) в виде . Вычисление начнем с произведения , затем суммы , далее произведения и т.д. Метод Горнера требует не более N операций умножения и N операций сложения.

Пример: пусть дан полином p(z) степени N = 4: p(z) = 4z⁴ - 2z³ + 3z² + z - 5.

p(z) = (4z³ – 2z² + 3z + 1)z – 5 = ((4z² – 2z + 3)z + 1)z – 5 = (((4z – 2)z + 3)z + 1)z – 5.

Пусть z = -1: 4·z = 4·(-1) = -4, -4 - 2 = -6, -6·z = -6·(-1) = 6, 6 + 3 = 9, 9·z = 9·(-1) = -9, -9 + 1 = -8, -8·z= = -8·(-1) = 8, 8 – 5 = 3.

Мультипликативная сложность = 4, аддитивная = 4. Если бы полином считался прямо, то мультипликативная сложность составила бы 6 операций.

Вычисление полинома в точках с помощью алгоритма «разделяй и властвуй»:

Пусть необходимо вычислить полином в нескольких точках а₁, а₂, …, а_k, k ≤ N. Положим сначала

z = a₁. Тогда можно записать p(z) = (z – a₁) q(z) + r(z), где q(z) и r(z) – частное и остаток от деления p(z) на (z – a₁). Этот результат можно распространить на большее число точек. Рассмотрим произведение и запишем p(z) = m(z) q(z) + r(z). В точке z = a_i полином m(z) равен нулю, поэтому p(a_i) = r(a_i). Теперь вычисление полинома p(z) свелось к вычислению полинома r(z), степень которого меньше.

Этот подход можно использовать для построения алгоритма вычисления полинома степени N – 1 в N точках. Положим N = 2^l. Разделим N точек на две половины и образуем полиномы

и . Разделим p(z) на m₁(z) и m₂(z). При этом получим остатки r₁(z) и r₂(z) степени N/2. Теперь осталось вычислить эти остатки в N/2 точках. Для вычисления остатков можно воспользоваться аналогичным приемом, повторяя его многократно.

Пример: Пусть требуется вычислить полином p(z) = 4z³ - 2z² - 2z + 1 в точках z, равных -2, 2, 1, -1.

Образуем m₁(z) = (z + 2)(z – 2) = z² - 4, m₂(z) = (z – 1)(z + 1) = z² - 1. После деления p(z) на m₁(z) и m₂(z) получим остатки r₁(z) = 14z - 7, r₂(z) = 2z - 1. Далее остатки следует поделить на соответствующие образующие части полиномов m₁(z) и m₂(z): r₁(z)/(z + 2) = -35 ⇒ p(-2) = -35. Аналогично получим p(2) = 21, p(-1) = -3, p(1) = 1.