1.2 Квантование электрического заряда. Элементарный заряд.

Элементарный электрический заряд, е, наименьший электрический заряд, известный в природе:

e = 1,602176462(63)×10 ^{– 19} Кл [2005].

На существование элементарного электрического заряда впервые с определённостью указал английский учёный Джордж Стони (Stoney George, 1874). Его гипотеза вытекала из установленных Майклом Фарадеем (Faraday Michael, 1833—34) законов электролиза.

Стони впервые (1881) вычислил величину электрического заряда одновалентного иона, равную е = F/N_A, где F - число Фарадея, N_A - число Авогадро.

Величина элементарного электрического заряда была установлена прямыми измерениями Робертом Милликеном (Millikan Robert, 1911).

Величина элементарного электрического заряда определяет константу электромагнитного взаимодействия

 = e²/₀ ћc = 7,297352533(27)×10 ^{– 3} ~ 1/137

и входит во все уравнения микроскопической электродинамики.

Элементарный электрический заряд в точности равен величине электрического заряда электрона, протона и почти всех других заряженных элементарных частиц, которые тем самым являются материальными носителями наименьшего заряда в природе.

Элементарный электрический заряд не может быть уничтожен; этот факт составляет содержание закона сохранения электрического заряда на микроскопическом уровне.

Существует положительный и отрицательный элементарный электрический заряд, причём элементарная частица и её античастица имеют заряды противоположных знаков. Электрический заряд любой микросистемы и макроскопических тел всегда равен целому кратному от величины е (или нулю).

Причина такого «квантования» заряда не установлена.

Одна из гипотез (Dirac Paul, 1931) основана на существовании магнитных монополей (монополей Дирака).

Почти все заряженные элементарные частицы имеют заряд е или -е (исключение - некоторые резонансы с зарядом, кратным е).

Свободные частицы с дробными электрическими зарядами не наблюдались.

В теории сильного взаимодействия - квантовой хромодинамике были предсказаны (Gell-Mann Murray, 1964) частицы (кварки) с зарядами, кратными (1/3)е. Эти частицы составляют структуру адронов (мезонов и барионов). Они существуют только в связанном состоянии (явление конфайнмента, пленения), образуя адроны.

Закон релятивистской инвариантности заряда (Lorentz Hendrik, 1877): заряд любого тела инвариантен относительно изменения системы отсчета. Следствие из этого закона: заряд тела не зависит от его скорости и ускорения.

1.3 Точечный и распределённый заряд.

В том случае, когда заряд распределен внутри макроскопического тела или некоторой области пространства, его пространственное расположение принято описывать с помощью: объемной плотности заряда (), поверхностной плотности заряда () и линейной плотности заряда (). Эти величины определяются формулами:

,

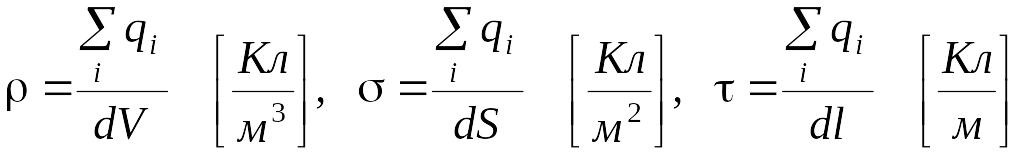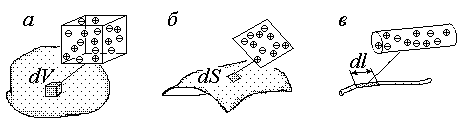
где суммируются заряды всех частиц в объеме dV, на площадке dS и отрезке dl, соответственно. Величины dV, dS, dl выбираются малыми (см. рис. 1.3.1) по сравнению с объемом (площадью, длиной) тела, но содержащим много элементарных заряженных частиц (электронов, ионов).

Рис.1.3.1

При разбиении заряженного тела объемом V на большое число N малых частей, каждая такая часть может быть рассмотрена как точечный заряд, напряженность поля которого dE_i, вычисляется по закону

dE_i = kdq(r′)(rr′)|rr′|^3

Применяя принцип суперпозиции для N, стремящегося к бесконечности, получаем напряженность тела как объемный интеграл:

.

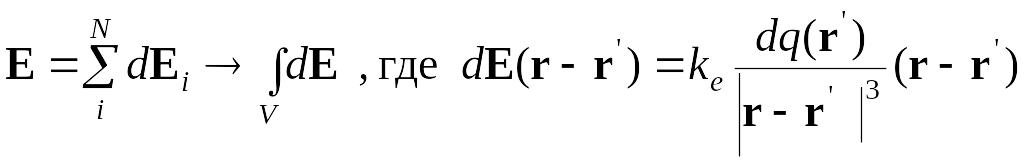А

Рис. 1.3.2

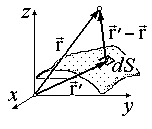
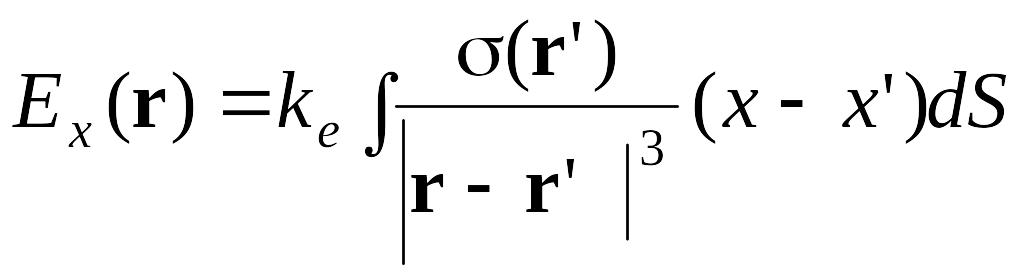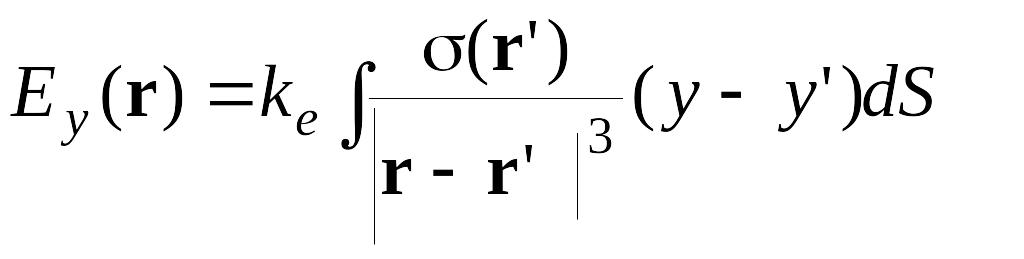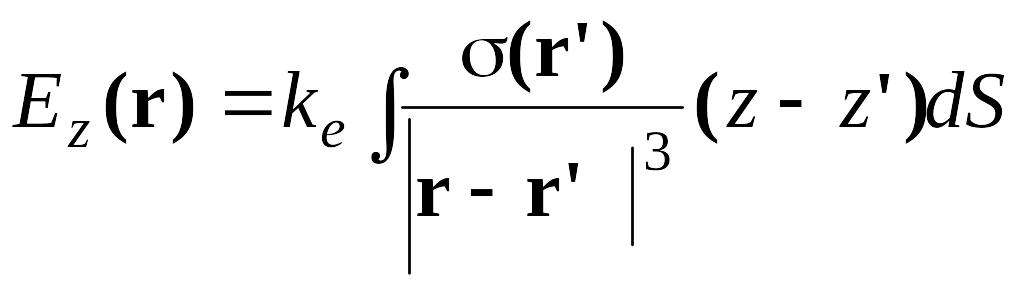налогично рассчитывают поля от заряженной поверхности (поверхностный интеграл) и от линейного заряженного тела (линейный интеграл). На рис.1.3.2 показан случай заряженной поверхности. Ниже приведены формулы расчета декартовых компонент напряженности по известной поверхностной плотности заряда s(r):

,

, .