11. Метод найменших квадратів (мнк). Система нормальних рівнянь.

Система нормальних рівнянь для визначення оцінок параметрів моделі 1МНК на основі покрокової регресії запишеться так:

Щоб побудувати таку систему нормальних рівнянь на основі 1МНК, необхідно стандартизувати (нормалізувати) дані так:

; .

При цьому середні значення і дорівнюють нулю, а дисперсії — одиниці.

12. Оператор оцінювання методу найменших квадратів (мнк) в матричному вигляді.

Оператор оцінювання параметрів моделі за 1МНК має вигляд:

де ; ; ;

— матриця, транспонована до матриці X.

Матриця X крім двох векторів незалежних змінних містить вектор одиниць. Він дописується в цій матриці ліворуч тоді, коли економетрична модель має вільний член.

13. Властивості оцінок параметрів, знайдених за методом найменших квадратів (мнк).

Оцінки параметрів є вибірковими характеристиками, що мають такі властивості:

1) незміщеності; (незміщеність — це мінімальна вимога, яка ставиться до оцінок параметрів . Якщо оцінка незміщена, то за багаторазового повторення випадкової вибірки навіть тоді, коли для окремих вибірок, можливо, оцінки були з похибкою, середнє значення цих похибок дорівнює нулю.)

2) ефективності; (вибіркові оцінки вектора параметрів А будуть ефективними тоді, коли їх дисперсії є найменшими. Величина дисперсії оцінок параметрів залежить від кількості спостережень, специфікації моделі та ефективного методу оцінювання цих параметрів. Це означає, що, припустившись помилки на будь-якому етапі при побудові економетричної моделі, можна дістати неефективні оцін­ки її параметрів.)

3) обґрунтованості; (обґрунтованість оцінки означає, що чим більші будуються вибірки, тим більша ймовірність того, що похибка оцінки не перевищуватиме достатньо малого значення e.)

4) інваріантності. (інваріантність оцінки базується на тому, що в разі перетворення параметрів А за допомогою деякої функції таке саме перетворення, виконане щодо , дає оцінку 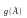нового параметра.)

14. Дисперсійний аналіз моделі лінійної множинної регресії.

Дисперсійний аналіз моделі здійснюється наступним чином:

D(Y)=D(Y*)+D(E)

D(Y)=

D(Y*)=

D(E)=

Sy²=

n – кількість спостережень, m – кількість регресорів;

S_E=

S =

15. Коефіцієнт множинної кореляції та детермінації та перевірка їх статистичної значущості.

R²=D(Y*)/D(Y) – коефіцієнт множинної детермінації

R=√ R² – коефіцієнт кореляції, -1≤R≤1

Множинний коефіцієнт кореляції:

Він характеризує тісноту зв’язку всіх пояснювальних змінних із залежною.

Для множинного коефіцієнта кореляції з урахуванням і без урахування кількості ступенів свободи характерна така сама зміна числового значення, як і для коефіцієнта детермінації.

Зауважимо, що не варто абсолютизувати високе значення , бо коефіцієнт детермінації може бути близьким до одиниці через те, що досліджувані показники (змінні) в моделі мають чітко виражений часовий тренд, який не стосується причинно-наслід­кових зв’язків. В економіці, як правило, такий тренд мають обсягові показники, подані в абсолютних одиницях.