19. Формула Остроградського-Гауса. Формула Стокса.

Формула Остроградського-Гауса.

Встановлює зв'язок між поверхневим інтегралом по замкненій поверхні і потрійним інтегралом по просторовій області, обмеженій цією поверхнею.

Нехай замкнена область G обмежена поверхнею σ, причому знизу та зверху обмежена гладкими поверхнями σ₁,σ₂, рівняння яких . Припустимо, що проекцією G на Оху є D. Нехай в області G визначено неперервну функцію R(x,y,z), яка в цій області має неперервну похідну . Розглянемо потрійний інтеграл

У правій частині рівності перший подвійний інтеграл запишемо за допомогою поверхневого інтегралу по зовнішній стороні поверхні σ₂, а другий – по зовнішній стороні поверхні σ₁. Враховуючи кути між нормаллю та віссю Oz, дістаємо:

Аналогічно, припустивши, що функції неперервні в області G, можна дістати формули:

Додавши почленно рівності (3), (4), (5), дістанемо:

– формула Остроградського-Гауса.

Справедлива для довільної області G, яку можна розбити на скінченне число підобластей, для яких виконуються рівності (8) – (10).

За допомогою цієї формули зручно обчислювати поверхневі інтеграли по замкнених поверхнях.

Формула Стокса

Формула Стокса встановлює зв'язок між поверхневим і криволінійним інтегралами. Нехай – поверхня, задана рівнянням , причому функції – неперервні в області – проекції поверхні на площину ; – контур, який обмежує , а – проекція контуру на площину , тобто – межа області .Виберемо верхню сторону поверхні

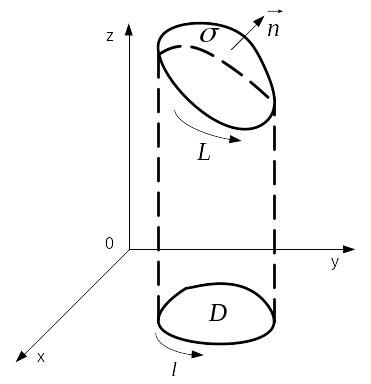
Поверхня

Якщо функція неперервна разом із своїми частинними похідними першого порядку на поверхні , то справедлива формула

Формула Стокса дає змогу обчислювати криволінійні інтеграли по замкнутих контурах за допомогою поверхневих інтегралів.

19. Скалярне поле. Характеристики скалярного поля. Градієнт.

Скалярне поле. Область простору, кожній точці М якої поставлено у відповідність значення деякої скалярної величини и (М), називають скалярним полем. Інакше кажучи, скалярне поле - це скалярна функція и (М) разом з областю її визначення.

Прикладами скалярних полів є поле температури даного тіла, поле густини даного неоднорідного середовища, поле вологості повітря, поле атмосферного тиску, поле потенціалів даного електростатичного поля тощо.

Для того щоб задати скалярне поле, досить задати скалярну функцію и (М) точки М і область її визначення.

Якщо функція и (М) не залежить від часу, то скалярне поле називають стаціонарним, а скалярне поле, яке змінюється з часом, - нестаціонарним. Надалі розглядатимемо лише стаціонарні поля.

Якщо в просторі ввести прямокутну систему координат Охуz, то точка М в цій системі матиме певні координати (х; у; z) і скалярне поле и стане функцією цих координат:

U=u( M ), u( x, y , z ) .

Градієнтом скалярного поля називається вектор-функція

.

Із рівності випливає, що

. Звідси , оскільки .

Тут – кут між векторами і в точці M. Очевидно, що має найбільше значення при , тобто у напрямі grad u u в даній точці. Інакше кажучи, вектор grad u в даній точці вказує напрям найбільшого зростання поля (функції ) у цій точці, а є швидкість зростання функції в цьому напрямі. Таким чином, вектор grad u не залежить від вибору системи координат, а його модуль і напрям у кожній точці визначається самою функцією U(M).