19. Криволінійні інтеграли другого роду вздовж просторових кривих.

20. Формула Гріна. Обчислення площі плоскої фігури через криволінійний інтеграл.

Зв'язок між подвійним інтегралом по області D і криволінійним інтегралом по межі L цієї області встановлює формула Гріна, яка широко застосовується в математичному аналізі. Нехай на площині Оху задана область D, обмежена кривою, яка перетинається з прямими, паралельними координатним осям не більше ніж в двох точках тобто область D — правильна.

Т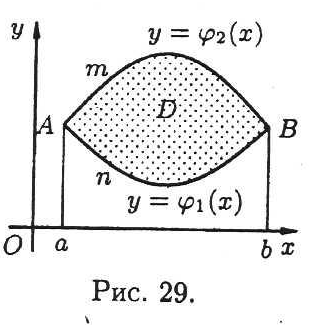 еорема. Якщо функції Р(х;у) і Q(х;у) неперервні разом зі своїми частинними похідними в області D, то має місце формула (2.8)

де L— межа області D і інтегрування уздовж кривої L,

проводиться в додатньому напрямі

Формула (2.8) називається формулою Гріна.

Нехай — рівняння дуги АnВ, а - рівняння дуги АmВ (Див. рис. 8). Знайдемо спочатку . За правилом обчислення подвійного інтеграла, маємо:

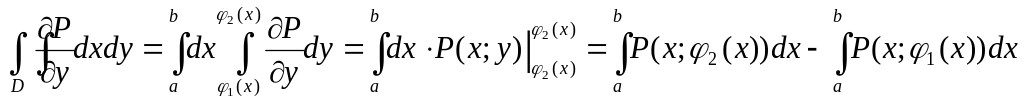
19. Поверхневі інтеграли першого роду: означення, обчислення.

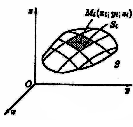
Узагальненням подвійного інтеграла є так званий поверхневий інтеграл. Нехай в точках деякої поверхні S, з площею S, простору Охуz визначена неперервна функція

f(х;у; z). Розіб'ємо поверхню S на n частин площі яких позначимо через (див. рис. 14), а діаметри — через , . В кожній частині візьмемо довільну точку і складемо суму:

(3.1) .

Вона називається інтегральною для функції по поверхні S.

Якщо інтегральна сума (3.1) має межу, то він називається поверхневим інтегралом I роду від функції f(х;у; z) по поверхні S і позначається:

Таким чином, за визначенням, (3.2)

Відзначимо, що якщо поверхня S гладка (в кожній її точці існує дотична площина, яка безперервно змінюється з переміщенням точки по поверхні), а функція (х; у; z) неперервна на цій поверхні, то поверхневий інтеграл існує (теорема існування)

Поверхневий інтеграл I роду володіє наступними властивостями:

1. ,де с — число.

2.

3. Якщо поверхню S розбити на частини S₁ і S₂ такі, що S = S₁ S₂, а перетин S₁ і S₂ складається лише з межі, що їх розділяє, то:

4. Якщо на поверхні S виконана нерівність то:

5. , де S- площа поверхні S;

6.

7. Якщо (х; у; z) неперервна на поверхні S, то на цій поверхні існує точка така, що:

(теорема про середнє значення).

Обчислення поверхневого інтеграла I роду

Обчислення поверхневого інтеграла I роду зводиться до обчислення подвійного інтеграла по області D) — проекції поверхні S на площину Оxу. Розіб'ємо поверхню S на частини . Позначимо через проекцію на площину Оxу. Отримуємо формулу:

(3.5)

що виражає інтеграл по поверхні S через подвійний інтеграл по проекції S на площину Оху.

19. Деякі застосування поверхневих інтегралів до механіки.

Площа поверхні

Якщо поверхня S задана рівнянням z = z(х;у), а її проекція на площину Оху є область D, в якій z(x;y), , — неперервні функції, то її площа S обчислюється по формулі: або

Крім того, поверхневий інтеграл застосовують для обчислення маси, координат центру мас, моментів інерції матеріальних поверхонь з відомою поверхневою густиною розподілу маси . Всі ці величини визначаються одним в тим же способом: дану область розбивають на кінцеве число «дрібних частин», роблячи для кожної області розподілу спрощуючи задачу припущенні; знаходять наближене значення шуканої величини; переходячи межі при необмеженому подрібненні області розподілу. Проілюструємо описаний спосіб на прикладі визначення маси матеріальної поверхні.

Маса поверхні

Про матеріальну поверхню відомо: густина розподілу маси . Тоді для знаходження маси поверхні:

1. Розбиваємо поверхню S на n частин S , і = 1,2,... n, площу якої позначимо

2. Беремо довільну точку М_і (х_і; у_і; z_i) в кожної області S . Припускаємо, що в межах області S густина постійна і рівна значенню її в точці М_і

З. Маса області S мало відрізняється від маси фіктивної однорідної області з постійною густиною

4. Підсумовуючи по всій області, одержуємо:

5. За точне значення маси матеріальної поверхні S приймається межа, якої прагне отримане наближене значення при прагненні до нуля діаметрів областей S тобто або

Моменти, центр тяжкості поверхні

Статистичні моменти, координати центру тяжкості, моменти інерції матеріальної поверхні S знаходяться по відповідних формулах: